Polytope 4181
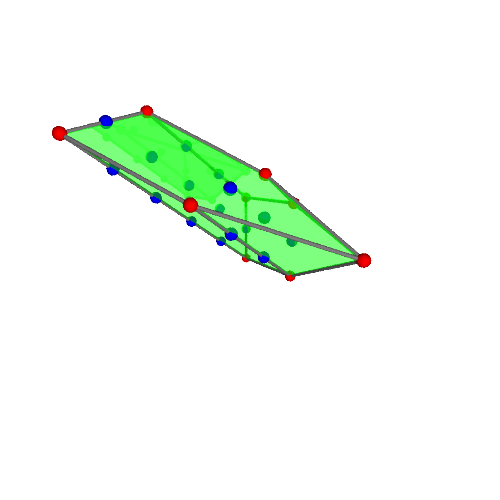
Image of polytope 4181 PALP id: 4181
grdb id: 72684
Integer points: [ 1 0 0 0 0 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 0 0 0 0 0]
[ 0 1 0 1 -2 -1 2 2 -3 0 1 -2 -1 0 1 2 -2 -1 0 1 -1 0 1 -1 0]
[ 0 0 1 -2 1 2 -1 -3 2 1 0 2 1 0 -1 -2 1 0 -1 -2 1 0 -1 0 -1]
Degree: 12
Hilbert function: 1 + 9 t + 35 t2 + 91 t3 + 189 t4 + 341 t5 + 559 t6 + 855 t7 + 1241 t8 + 1729 t9 + 2331 t10 + ...
Polynomials:
Period sequence Fano variety Laurent polynomial
7 rank 1, V12 x + y + z + 3*y*z-1 + x-1*y2*z-1 + 3*x-1*y + 2*y-1*z + 3*x-1*z + x-1*y-1*z2 + y*z-2 + 2*x-1*y2*z-2 + 3*z-1 + 8*x-1*y*z-1 + 3*y-1 + 12*x-1 + y-2*z + 8*x-1*y-1*z + 2*x-1*y-2*z2 + x-1*y2*z-3 + 5*x-1*y*z-2 + 10*x-1*z-1 + 10*x-1*y-1 + 5*x-1*y-2*z + x-1*y-3*z2
7 rank 1, V12 x + y + z + 2*y*z-1 + x-1*y2*z-1 + 3*x-1*y + 3*y-1*z + 3*x-1*z + x-1*y-1*z2 + y*z-2 + 2*x-1*y2*z-2 + 3*z-1 + 8*x-1*y*z-1 + 3*y-1 + 12*x-1 + y-2*z + 8*x-1*y-1*z + 2*x-1*y-2*z2 + x-1*y2*z-3 + 5*x-1*y*z-2 + 10*x-1*z-1 + 10*x-1*y-1 + 5*x-1*y-2*z + x-1*y-3*z2
11 rank 2, number 6 x + y + z + 2*y*z-1 + x-1*y2*z-1 + 3*x-1*y + 2*y-1*z + 3*x-1*z + x-1*y-1*z2 + y*z-2 + 2*x-1*y2*z-2 + 3*z-1 + 8*x-1*y*z-1 + 3*y-1 + 12*x-1 + y-2*z + 8*x-1*y-1*z + 2*x-1*y-2*z2 + x-1*y2*z-3 + 5*x-1*y*z-2 + 10*x-1*z-1 + 10*x-1*y-1 + 5*x-1*y-2*z + x-1*y-3*z2
22 rank 3, number 1 x + y + z + 3*y*z-1 + x-1*y2*z-1 + 3*x-1*y + 3*y-1*z + 3*x-1*z + x-1*y-1*z2 + y*z-2 + 2*x-1*y2*z-2 + 3*z-1 + 8*x-1*y*z-1 + 3*y-1 + 12*x-1 + y-2*z + 8*x-1*y-1*z + 2*x-1*y-2*z2 + x-1*y2*z-3 + 5*x-1*y*z-2 + 10*x-1*z-1 + 10*x-1*y-1 + 5*x-1*y-2*z + x-1*y-3*z2
Facets:
Facet Multiplicity Admissible lattice Minkowksi decompositions
Image of facet 0 1 irreducible and admissible
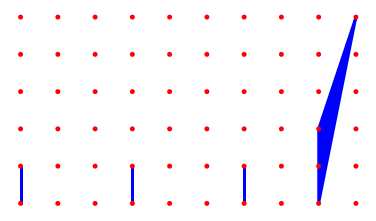
Image of facet 146 1 Lattice Minkowski decompositions of facet 146
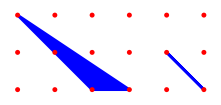
Image of facet 20 1 Lattice Minkowski decompositions of facet 20
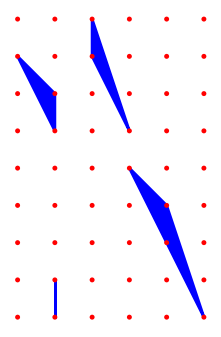
Image of facet 23 2 Lattice Minkowski decompositions of facet 23
Image of facet 216 1 Lattice Minkowski decompositions of facet 216
Image of facet 9 1 irreducible and admissible
previous:polytope 4180
next:polytope 4182