Fano Varieties
Legend for period sequences:
n/a – known, and not one of 165 from Minkowski list, [7 entries]
# – known to be number # from Minkowski list, [91 entries]
A# – known to be number # from Minkowski list, computed with A/NA corr., [5 entries]
?*# – unknown, but STD ansatz predicts it is number #, [1 entry]
? – unknown and no guess. [0 entries]
Rank 1 Fano 3-folds
| Name |
Fano index |
Period sequence |
Construction |
 |
4 |
12 |
projective 3-space |
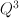 |
3 |
4 |
the quadric 3-fold |
 |
2 |
14 |
a linear section of 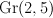 |
 |
2 |
2 |
a (2,2) complete intersection in 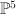 |
 |
2 |
0 |
the cubic 3-fold |
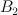 |
2 |
1 |
a quartic in 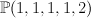 |
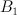 |
2 |
n/a |
a sextic in 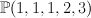 |
 |
1 |
n/a |
a sextic in 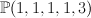 |
 |
1 |
15 |
a quartic in 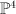 |
 |
1 |
19 |
a (2,3) complete intersection in 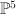 |
 |
1 |
5 |
a (2,2,2) complete intersection in  |
 |
1 |
9 |
section of 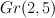 by intersection of quadric and linear space by intersection of quadric and linear space |
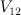 |
1 |
7 |
linear section of spinor variety 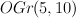 |
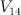 |
1 |
18 |
linear section of 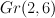 |
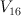 |
1 |
20 |
linear section of 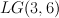 |
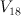 |
1 |
10 |
linear section of 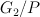 |
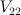 |
1 |
17 |
section of triple universal bundle on 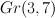 |
Rank 2 Fano 3-folds
| Number |
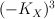 |
Period sequence |
Description |
| 1 |
4 |
n/a |
the blow-up of 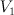 with centre an elliptic curve which is the intersection of two members of with centre an elliptic curve which is the intersection of two members of 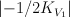 |
| 2 |
6 |
n/a |
a double cover of  branched along a divisor of bidegree (2,4) branched along a divisor of bidegree (2,4) |
| 3 |
8 |
n/a |
the blow up of 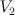 with centre an elliptic curve which is the intersection of two elements of with centre an elliptic curve which is the intersection of two elements of 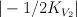 |
| 4 |
10 |
49 |
the blow up of  with centre an intersection of two cubics with centre an intersection of two cubics |
| 5 |
12 |
34 |
the blow up of 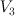 with centre a plane cubic on it with centre a plane cubic on it |
| 6 |
12 |
11 |
a divisor of bidegree (2,2) in 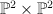 |
| 7 |
14 |
51 |
the blow up of a quadric  with centre the intersection of two members of with centre the intersection of two members of 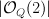 |
| 8 |
14 |
26 |
a double cover of 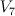 with branch locus a member with branch locus a member 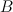 of of 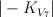 such that such that 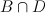 is smooth, where is smooth, where 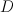 is the exceptional divisor of the blow-up is the exceptional divisor of the blow-up 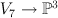 |
| 9 |
16 |
62 |
the blow up of  in a curve in a curve  of degree 7 and genus 5 of degree 7 and genus 5 |
| 10 |
16 |
40 |
the blow up of 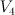 with centre an elliptic curve which is the intersection of two hyperplane sections with centre an elliptic curve which is the intersection of two hyperplane sections |
| 11 |
18 |
56 |
the blow up of 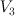 with centre a line on it with centre a line on it |
| 12 |
20 |
13 |
the blow up of  in a curve in a curve  of degree 6 and genus 3 of degree 6 and genus 3 |
| 13 |
20 |
52 |
the blow-up of a 3-dimensional quadric  in a curve in a curve  of genus 2 and degree 6 of genus 2 and degree 6 |
| 14 |
20 |
A 39 |
the blow-up of 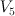 with center an elliptic curve which is an intersection of two hyperplane sections with center an elliptic curve which is an intersection of two hyperplane sections |
| 15 |
22 |
35 |
the blow-up of  with center the intersection of a quadric and a cubic with center the intersection of a quadric and a cubic |
| 16 |
22 |
59 |
the blow-up of 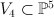 with center a conic on it with center a conic on it |
| 17 |
24 |
A 38 |
the blow-up of a 3-dimensional quadric  with center an elliptic curve of degree 5 on it with center an elliptic curve of degree 5 on it |
| 18 |
24 |
60 |
a double cover of  with branch locus a divisor of bidegree (2,2) with branch locus a divisor of bidegree (2,2) |
| 19 |
26 |
55 |
the blow-up of 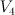 with center a line on it with center a line on it |
| 20 |
26 |
A 46 |
the blow-up of 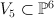 with center a twisted cubic on it with center a twisted cubic on it |
| 21 |
28 |
A 8 |
the blow-up of 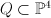 with center a twisted quartic on it (a smooth rational curve of degree 4 which spans with center a twisted quartic on it (a smooth rational curve of degree 4 which spans 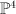 ) ) |
| 22 |
30 |
A 50 |
the blow-up of 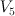 with center a conic on it with center a conic on it |
| 23 |
30 |
29 |
the blow-up of a quadric with center an intersection of 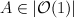 and and 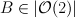 |
| 24 |
30 |
66 |
A divisor of bidegree (1,2) on 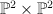 |
| 25 |
32 |
28 |
The blow up of  with centre an elliptic curve which is the complete intersection of two quadrics with centre an elliptic curve which is the complete intersection of two quadrics |
| 26 |
34 |
?*47 |
the blow up of 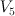 with center a line on it with center a line on it |
| 27 |
38 |
61 |
the blow up of  with center a twisted cubic with center a twisted cubic |
| 28 |
40 |
33 |
the blow-up of  with centre a plane cubic with centre a plane cubic |
| 29 |
40 |
42 |
the blow-up of a quadric 3-fold  with centre a conic on it with centre a conic on it |
| 30 |
46 |
70 |
the blow-up of  with center a conic with center a conic |
| 31 |
46 |
48 |
the blow-up of a quadric 3-fold  with center a line on it with center a line on it |
| 32 |
48 |
6 |
a divisor 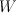 on on 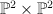 of bidegree of bidegree 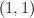 |
| 33 |
54 |
54 |
the blow-up of  with center a line with center a line |
| 34 |
54 |
44 |
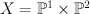 |
| 35 |
56 |
30 |
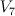 , which is the blow-up of , which is the blow-up of  at a point at a point |
| 36 |
62 |
58 |
the scroll 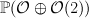 over over  |
Rank 3 Fano 3-folds
| Number |
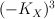 |
Period sequence |
Description |
| 1 |
12 |
22 |
a double cover of  with branch locus a divisor of tridegree (2,2,2) with branch locus a divisor of tridegree (2,2,2) |
| 2 |
14 |
97 |
a member of 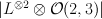 on the on the  -bundle -bundle 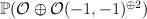 over over 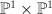 , where , where  is the tautological line bundle is the tautological line bundle |
| 3 |
18 |
31 |
a divisor on 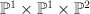 of tridegree of tridegree 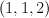 |
| 4 |
18 |
151 |
the blow-up of 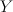 (rank 2 table, number 18) with center a smooth fiber of (rank 2 table, number 18) with center a smooth fiber of 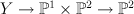 , where the first map is the double cover and the second map is the projection , where the first map is the double cover and the second map is the projection |
| 5 |
20 |
109 |
the blow-up of  with center a curve of bidegree (5,2) that projects isomorphically to a conic in with center a curve of bidegree (5,2) that projects isomorphically to a conic in  |
| 6 |
22 |
146 |
the blow-up of  with center a disjoint union of a line and an elliptic curve of degree 4 with center a disjoint union of a line and an elliptic curve of degree 4 |
| 7 |
24 |
36 |
the blow-up  of of 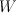 with center an elliptic curve which is a complete intersection of two members of with center an elliptic curve which is a complete intersection of two members of 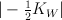 |
| 8 |
24 |
85 |
a member of the linear system 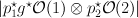 on on 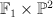 , where , where 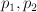 are the projections and are the projections and  is the blow-up is the blow-up |
| 9 |
26 |
68 |
the blow-up of the cone 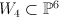 over the Veronese surface over the Veronese surface 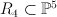 with center a disjoint union of the vertex and a quartic in with center a disjoint union of the vertex and a quartic in 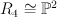 |
| 10 |
26 |
67 |
the blow-up of 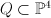 with center a disjoint union of two conics on it with center a disjoint union of two conics on it |
| 11 |
28 |
107 |
the blow-up  of of 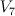 with center a complete intersection of two general members of with center a complete intersection of two general members of 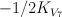 |
| 12 |
28 |
144 |
the blow-up of  with centre a disjoint union of a twisted cubic and a line with centre a disjoint union of a twisted cubic and a line |
| 13 |
30 |
16 |
the blow-up |
| 14 |
32 |
148 |
the blow-up |
| 15 |
32 |
112 |
the blow-up  of a quadric of a quadric 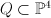 with center the disjoint union of a line on with center the disjoint union of a line on  and a conic on and a conic on  |
| 16 |
34 |
119 |
the blow-up |
| 17 |
36 |
37 |
a smooth divisor on 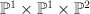 of tridegree of tridegree 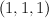 |
| 18 |
36 |
160 |
the blow-up |
| 19 |
38 |
57 |
the blow-up |
| 20 |
38 |
63 |
the blow-up |
| 21 |
38 |
98 |
the blow-up of  along a curve of bidegree (2,1) along a curve of bidegree (2,1) |
| 22 |
40 |
152 |
the blow-up of  along a curve of bidegree (0,2), that is a conic in along a curve of bidegree (0,2), that is a conic in 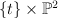 |
| 23 |
42 |
158 |
the blow-up |
| 24 |
42 |
86 |
the fiber product 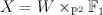 where where 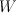 is a (1,1) hypersurface in is a (1,1) hypersurface in 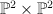 |
| 25 |
44 |
41 |
the blow-up |
| 26 |
46 |
113 |
the blow-up  of of  with center a disjoint union of a point and a line with center a disjoint union of a point and a line |
| 27 |
48 |
21 |
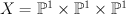 |
| 28 |
48 |
90 |
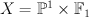 |
| 29 |
50 |
163 |
the blow-up |
| 30 |
50 |
84 |
the blow-up |
| 31 |
52 |
53 |
the blow-up |
Rank 4 Fano 3-folds
| Number |
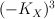 |
Period sequence |
Description |
| 1 |
24 |
3 |
a smooth divisor on 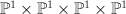 of polydegree of polydegree 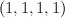 |
| 2 |
28 |
32 |
|
| 3 |
30 |
122 |
|
| 4 |
32 |
103 |
|
| 5 |
32 |
147 |
|
| 6 |
34 |
65 |
|
| 7 |
36 |
69 |
|
| 8 |
38 |
105 |
|
| 9 |
40 |
102 |
|
| 10 |
42 |
142 |
|
| 11 |
44 |
93 |
|
| 12 |
46 |
150 |
|
| 13 |
26 |
88 |
blowup of curve of tridegree 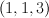 on on  |
Rank 5 Fano 3-folds
| Number |
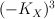 |
Period sequence |
Description |
| 1 |
28 |
114 |
|
| 2 |
36 |
87 |
“smooth toric, but not 5-3” |
| 3 |
36 |
43 |
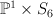 |
Fano 3-folds with 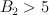
| Picard number |
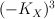 |
Period sequence |
Description |
| 6 |
30 |
64 |
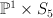 |
| 7 |
24 |
71 |
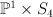 |
| 8 |
18 |
45 |
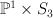 |
| 9 |
12 |
n/a |
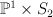 |
| 10 |
6 |
n/a |
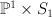 |
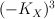
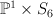
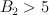
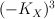
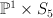
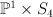
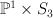
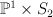
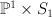

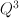
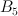
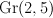
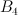
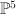

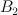
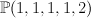
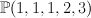
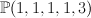
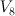


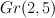 by intersection of quadric and linear space
by intersection of quadric and linear space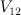
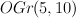
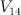
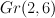
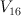
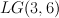
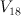
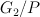
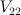
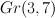
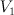 with centre an elliptic curve which is the intersection of two members of
with centre an elliptic curve which is the intersection of two members of 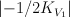
 branched along a divisor of bidegree (2,4)
branched along a divisor of bidegree (2,4)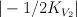
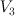 with centre a plane cubic on it
with centre a plane cubic on it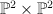
 with centre the intersection of two members of
with centre the intersection of two members of 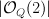
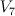 with branch locus a member
with branch locus a member 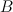 of
of 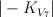 such that
such that 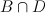 is smooth, where
is smooth, where 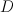 is the exceptional divisor of the blow-up
is the exceptional divisor of the blow-up 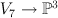
 of degree 7 and genus 5
of degree 7 and genus 5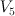 with center an elliptic curve which is an intersection of two hyperplane sections
with center an elliptic curve which is an intersection of two hyperplane sections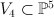 with center a conic on it
with center a conic on it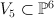 with center a twisted cubic on it
with center a twisted cubic on it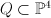 with center a twisted quartic on it (a smooth rational curve of degree 4 which spans
with center a twisted quartic on it (a smooth rational curve of degree 4 which spans 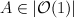 and
and 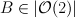
 on
on 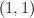
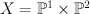
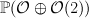 over
over 
 with branch locus a divisor of tridegree (2,2,2)
with branch locus a divisor of tridegree (2,2,2)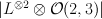 on the
on the 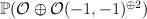 over
over 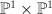 , where
, where  is the tautological line bundle
is the tautological line bundle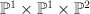 of tridegree
of tridegree 
 (rank 2 table, number 18) with center a smooth fiber of
(rank 2 table, number 18) with center a smooth fiber of 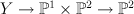 , where the first map is the double cover and the second map is the projection
, where the first map is the double cover and the second map is the projection of
of 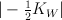
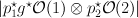 on
on 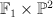 , where
, where 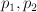 are the projections and
are the projections and  is the blow-up
is the blow-up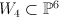 over the Veronese surface
over the Veronese surface 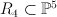 with center a disjoint union of the vertex and a quartic in
with center a disjoint union of the vertex and a quartic in 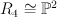
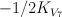
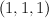
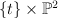
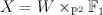 where
where 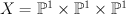
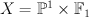
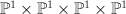 of polydegree
of polydegree 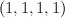
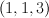 on
on
There is a discrepancy between tables 1 and 2:
in table 2 everywhere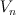 should be replaced with
should be replaced with 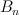 .
.
There are 49 period sequences with N=4.
45 of them correspond to Fano threefolds and (and all these threefolds have expected N equal to 4, except for one case – 4.7 and period sequence 69).
Fano variety 4.7 (period sequence 69) contradicts to expected N (from Matsuki).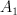 symmetry, so expected N is 5, while for this period sequence expected N is 4.
symmetry, so expected N is 5, while for this period sequence expected N is 4.
Matsuki says it has just
And This comment explains that remaining 4 period sequences (23, 24, 25 and 27) are parasitic.