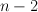September 22, 2010, 12:09 pm
Here are my (incomplete) notes from Batyrev’s talk in the Extremal Laurent Polynomials workshop at Imperial:
Batyrev_London_Sep_2010
If you have complete notes, please post them here.
Partial summary:
- spherical varieties
- a model family of examples:
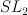 -varieties
-varieties
- review: compactification and toric varieties
- spherical compactification in these examples
- valuations and coloured cones
- finding toric degenerations
September 22, 2010, 12:04 pm
Here are my notes from Altmann’s talk at the Extremal Laurent Polynomials workshop at Imperial:
Altmann_London_Sep_2010
Summary:
- an example due to Pinkham
- deformations and Minkoski sums; a lattice condition
- constructing the deformation corresponding to a Minkwoski decomposition
- the versal deformation space and the moduli space of generalized Minkowski summands of Q
- Example: the cone over a hexagon
- the equations defining the versal deformation space in the isolated Gorenstein case
- a new point of view: double divisors
September 22, 2010, 11:58 am
Here are my notes from Siebert’s talk at the Extremal Laurent Polynomials workshop at Imperial:
Siebert_London_Sep_2010
Summary:
- An overview of toric degenerations and the Gross–Siebert picture
- Examples: a pencil of quartics in
 and a pencil of elliptic curves in
and a pencil of elliptic curves in 
- the Gross–Siebert Reconstruction Theorem
- Mirror Symmetry and the discrete Legendre Transform
- Landau–Ginzburg models; the Hori–Vafa mirror
- how to extend the superpotential from the central fiber to the whole of the mirror family in such a way that the resulting superpotential is proper
- Example:
 , flattening the boundary of the polyhedral complex
, flattening the boundary of the polyhedral complex
- Broken lines and scattering
September 22, 2010, 11:50 am
Here are my notes from Golshev’s talk at the Extremal Laurent Polynomials workshop at Imperial:
Golyshev_London_Sep_2010
Summary:
- a historical analogy: the study of Fano varieties now versus the study of algebraic varieties in the early 1970s
- the key idea: classifying Fanos by detecting and classifying Fano quantum motives and their realizations
- possible approaches
- the Tannakian picture
- the quantum Satake correspondence (Golyshev–Manivel)
- two steps in this direction: Ueda’s proof of the Dubrovin Conjecture for
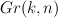 ; Galkin–Golyshev–Iritani’s proof that Apery=Gamma
; Galkin–Golyshev–Iritani’s proof that Apery=Gamma
- irregular monodromy data for Dubrovin’s quantum connection
- the Extended Dubrovin Conjecture and the Apery=Gamma hypothesis
- the Extended Dubrovin Conjecture and the Apery=Gamma hypothesis hold for
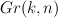
September 22, 2010, 11:30 am
Here are my notes from Manivel’s talk in Bonn:
Manivel_Bonn_Sep_2010
Summary:
- geometric Satake after Drinfeld and Ginzburg
- example:
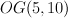
- the quantum Chevalley formula (Fulton–Woodward)
- cohomology of G/P in general
- cohomology of G/P: improvements in the miniscule case
- semisimplicity of
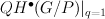 (Chaput–Manivel–Perrin) and connections to work of Kostant (Gorbunov–Petrov)
(Chaput–Manivel–Perrin) and connections to work of Kostant (Gorbunov–Petrov)
- quantum Satake for miniscule type-D Grassmannians
September 22, 2010, 11:23 am
Here are my notes from Golyshev’s second talk in Bonn:
Golyshev_2_Bonn_Sep_2010
Summary:
- the “spin representation of K3” and its quantum analog
- some evidence: the Bertram–Ciocan-Fontanine–Kim result for
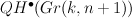
- the geometric Satake correspondence (Drinfeld–Ginzburg)
- miniscule Grassmannians as smooth
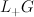 -orbits in the affine Grassmannian
-orbits in the affine Grassmannian
- a quantum analog of geometric Satake in this case
September 22, 2010, 11:17 am
Here are my notes from Kresch’s talk in Bonn:
Kresch_Bonn_Sep_2010
Summary:
- the orthogonal Grassmannian
- Schubert varieties are indexed by strict partitions
- special Schubert classes
- ring presentations for
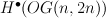 and
and 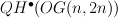
- the connection to algebraic combinatorics via Praguez-Rataiski polynomials
- quantum Giambelli and quantum Pieri (Kresch-Tamvarkis)
September 22, 2010, 11:13 am
Here are my notes from Katzarkov’s talk in Bonn:
Katzarkov_Bonn_Sep_2010
Summary:
- Clemens-Griffiths showed that the 3-dimensional cubic is not rational by showing that its intermediate Jacobian is not the Jacobian of a curve; we suggest analogs of this.
- Homological Mirror Symmetry and the perverse sheaf of vanishing cycles
- detecting rationality via monodromy properties on the LG mirror (Gross-Katzarkov, Pryzalkowski, Golyshev)
- spectra of triangulated categories; examples
- Theorem:
 is rational of dimension
is rational of dimension 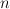 implies that the spectrum of
implies that the spectrum of 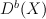 has no gaps of size greaeter than
has no gaps of size greaeter than 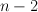
- the outlook for 4-dimensional cubics
September 22, 2010, 11:07 am
Here are my notes from Golyshev’s talk in Bonn.
Golyshev_1_Bonn_Sep_2010
Summary:
- a historical analogy: the study of Fano varieties now versus algebraic number theory prior to the proof of the Weil Conjectures
- linearization and motives
- Tannakian categories
- the “quantum Tannakian category”
- realizations in algebraic number theory: one can detect algebraic varieties by detecting their motives (in practice by detecting their L-functions via Selberg-Stark)
- the “quantum Tate realization” and quantum detection
- the Satake correspondence and its quantum parallel
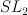 -varieties
-varieties and a pencil of elliptic curves in
and a pencil of elliptic curves in 
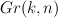 ; Galkin–Golyshev–Iritani’s proof that Apery=Gamma
; Galkin–Golyshev–Iritani’s proof that Apery=Gamma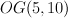
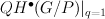 (Chaput–Manivel–Perrin) and connections to work of Kostant (Gorbunov–Petrov)
(Chaput–Manivel–Perrin) and connections to work of Kostant (Gorbunov–Petrov)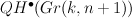
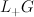 -orbits in the affine Grassmannian
-orbits in the affine Grassmannian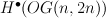 and
and 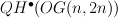
 is rational of dimension
is rational of dimension 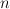 implies that the spectrum of
implies that the spectrum of 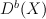 has no gaps of size greaeter than
has no gaps of size greaeter than