V. Batyrev: “Toric Deformations of Some Spherical Fano Varieties”
Here are my (incomplete) notes from Batyrev’s talk in the Extremal Laurent Polynomials workshop at Imperial:
If you have complete notes, please post them here.
Partial summary:
- spherical varieties
- a model family of examples:
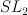-varieties - review: compactification and toric varieties
- spherical compactification in these examples
- valuations and coloured cones
- finding toric degenerations
Maybe it worth to note.
Yuri Prokhorov explianed to me that 2.21 with involution is actually a spherical variety – it has finite number of orbits with respect to
.
Construction is the following (http://books.google.com/books?id=iZOJuKZTEJkC&lpg=PA137&ots=OTpkhewIeD&dq=Tetsuo%20Nakano%20%22equivariant%20completions%22&lr&hl=ru&pg=PA143#v=onepage&q=Tetsuo%20Nakano%20%22equivariant%20completions%22&f=false):
Projective line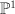
is embedded by linear system 
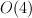into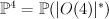 
,
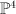preserving its image (twisted quartic C).
and its automorphism group acts on
In fact it is just 4th symmetric power of tautological representation.
Choose a generic invariant of degree $2$ i.e. smooth three-dimensional quadric Q that contains C and is G-invariant.
Then blowup of Q in C is a Fano threefold V of type 2.21 with action of G, the other contraction is also G-invariant and hence isomorphic to the original one,
so automorphisms of V are extended from G by an involution.
Numerous toric degenerations of spherical varieties were constructed by Alexeev and Brion,
however I don’t know if there is a theorem describing quantum multiplication by $c_1$ for spherical varieties.
Morally it should be possible to do using same technique as for toric and homogeneous varieties – just localize curves to B-invariant,
but have anybody already wrote on this? Could it be in the missing part of the talk?