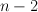September 22, 2010, 11:30 am
Here are my notes from Manivel’s talk in Bonn:
Manivel_Bonn_Sep_2010
Summary:
- geometric Satake after Drinfeld and Ginzburg
- example:
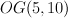
- the quantum Chevalley formula (Fulton–Woodward)
- cohomology of G/P in general
- cohomology of G/P: improvements in the miniscule case
- semisimplicity of
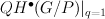 (Chaput–Manivel–Perrin) and connections to work of Kostant (Gorbunov–Petrov)
(Chaput–Manivel–Perrin) and connections to work of Kostant (Gorbunov–Petrov)
- quantum Satake for miniscule type-D Grassmannians
September 22, 2010, 11:23 am
Here are my notes from Golyshev’s second talk in Bonn:
Golyshev_2_Bonn_Sep_2010
Summary:
- the “spin representation of K3” and its quantum analog
- some evidence: the Bertram–Ciocan-Fontanine–Kim result for
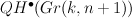
- the geometric Satake correspondence (Drinfeld–Ginzburg)
- miniscule Grassmannians as smooth
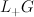 -orbits in the affine Grassmannian
-orbits in the affine Grassmannian
- a quantum analog of geometric Satake in this case
September 22, 2010, 11:17 am
Here are my notes from Kresch’s talk in Bonn:
Kresch_Bonn_Sep_2010
Summary:
- the orthogonal Grassmannian
- Schubert varieties are indexed by strict partitions
- special Schubert classes
- ring presentations for
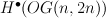 and
and 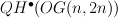
- the connection to algebraic combinatorics via Praguez-Rataiski polynomials
- quantum Giambelli and quantum Pieri (Kresch-Tamvarkis)
September 22, 2010, 11:13 am
Here are my notes from Katzarkov’s talk in Bonn:
Katzarkov_Bonn_Sep_2010
Summary:
- Clemens-Griffiths showed that the 3-dimensional cubic is not rational by showing that its intermediate Jacobian is not the Jacobian of a curve; we suggest analogs of this.
- Homological Mirror Symmetry and the perverse sheaf of vanishing cycles
- detecting rationality via monodromy properties on the LG mirror (Gross-Katzarkov, Pryzalkowski, Golyshev)
- spectra of triangulated categories; examples
- Theorem:
 is rational of dimension
is rational of dimension 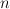 implies that the spectrum of
implies that the spectrum of 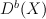 has no gaps of size greaeter than
has no gaps of size greaeter than 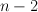
- the outlook for 4-dimensional cubics
September 22, 2010, 11:07 am
Here are my notes from Golyshev’s talk in Bonn.
Golyshev_1_Bonn_Sep_2010
Summary:
- a historical analogy: the study of Fano varieties now versus algebraic number theory prior to the proof of the Weil Conjectures
- linearization and motives
- Tannakian categories
- the “quantum Tannakian category”
- realizations in algebraic number theory: one can detect algebraic varieties by detecting their motives (in practice by detecting their L-functions via Selberg-Stark)
- the “quantum Tate realization” and quantum detection
- the Satake correspondence and its quantum parallel
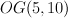
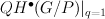 (Chaput–Manivel–Perrin) and connections to work of Kostant (Gorbunov–Petrov)
(Chaput–Manivel–Perrin) and connections to work of Kostant (Gorbunov–Petrov)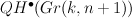
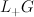 -orbits in the affine Grassmannian
-orbits in the affine Grassmannian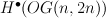 and
and 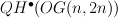
 is rational of dimension
is rational of dimension 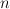 implies that the spectrum of
implies that the spectrum of 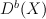 has no gaps of size greaeter than
has no gaps of size greaeter than