Fano Varieties and Extremal Laurent Polynomials

The updated script for computing Picard lattices of Fano threefolds: now it works and, even better, computes all five principal invariants of the smoothing!

Picard lattices of ambiguous nodal toric Fano threefolds

Let be a nodal toric Fano threefold (recall that in toric world terminal Gorenstein singularities of Fano threefolds are simply ordinary double points aka nodes ).

Given a terminal Gorenstein toric Fano threefold ,

this script do the following:

1. Compute Picard lattice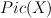
2. Then compute (self)intersection theory on this lattice.
This part is done in 3 steps:
a. pick a small crepant resolution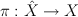
b. compute intersection theory of smooth toric manifold ,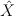
c. restrict intersection theory from 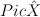to .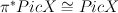

3. Threefold X has a unique deformation class of smoothing by Fano threefold Y
We also compute the principal invariants of Y: Betti numbers, degree, Lefschetz discriminant and Fano index

The main procedure is called Picard(toric)
The input is a 3-component vector toric=[description, vertices, faces]
description is a verbal description of variety X (not used for computations)
vertices is a matrix of vertices of the fan polytope Delta(X)
faces is a transposed matrix of faces (vertices of the moment polytope)

The output is a 2-component vector o = [lattice, invariants]
where lattice is 3-component vector [cubic, M, class]
cubic is homogenous cubic polynomial of ‘rk Pic(X)’ variables (self-intersection pairing)
class is the expression of the first Chern class in terms of generators of Picard group
M is the matrix of the Lefschetz pairing
and invariants is 5-component vector [rho,deg,b,d,r] of the principal invariants
rho is Picard number i.e. second Betti number of X
deg is the anticanonical degree
b is the half of third Betti number of the smoothing Y
d is the Lefschetz discriminant (i.e. determinant of matrix M)
r is the Fano index (i.e. divisibility of in 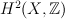)