Rank 3 Fano 3-folds
- a double cover of
 branched along a divisor of tridegree (2,2,2). This is a hypersurface of type
branched along a divisor of tridegree (2,2,2). This is a hypersurface of type 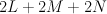 in the toric variety with weight data:
in the toric variety with weight data:
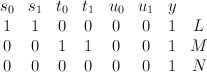
Quantum Lefschetz gives:
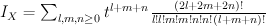
and regularizing gives period sequence 22:
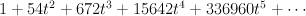
Note that this is a G-Fano. - a member of
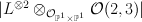 on the
on the  -bundle
-bundle 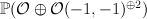 over
over 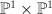 such that
such that  is irreducible, where
is irreducible, where  is the tautological line bundle and
is the tautological line bundle and 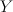 is a member of
is a member of 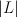 . As discussed here, this is period sequence 97.
. As discussed here, this is period sequence 97.
We do not understand this variety: in particular it does not seem to be Fano.Write
 for the ambient
for the ambient  -bundle, which is the toric variety with weight data:
-bundle, which is the toric variety with weight data:
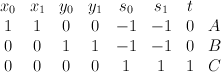
The line bundle is
is 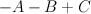 , so
, so  is a member of
is a member of 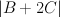 and
and 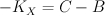 . The equation defining
. The equation defining  takes the form:
takes the form:
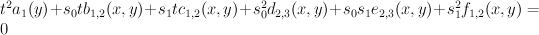
where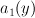 a linear function of
a linear function of  ;
; 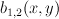 and
and 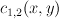 are homogeneous functions of
are homogeneous functions of 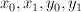 of bidegrees (1,2) in the
of bidegrees (1,2) in the 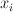 and
and 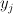 ; and
; and 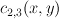 ,
, 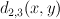 , and
, and 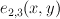 are homogeneous functions of
are homogeneous functions of 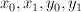 of bidegrees (2,3) in the
of bidegrees (2,3) in the 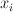 and
and 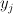 Consider now the subvariety
Consider now the subvariety  defined by the equations
defined by the equations 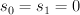 in
in  . This is a copy of
. This is a copy of 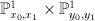 ; note that
; note that 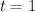 on
on 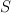 . The variety
. The variety  meets
meets 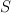 in the curve
in the curve  cut out by the equation
cut out by the equation 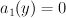 inside
inside 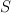 . Without loss of generality we can take
. Without loss of generality we can take 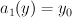 , so that on
, so that on  we have
we have  and
and 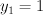 . The curve
. The curve  is a copy of
is a copy of 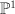 . We have that
. We have that 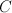 is trivial on
is trivial on  (because the section
(because the section 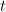 of
of 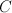 is non-vanishing on
is non-vanishing on  ) and that
) and that 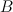 is also trivial on
is also trivial on  (because the section
(because the section 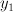 of
of 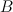 is non-vanishing on
is non-vanishing on  ). Thus
). Thus 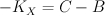 is trivial on
is trivial on  , and so
, and so  is not Fano.
is not Fano.
- a divisor on
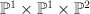 of tridegree
of tridegree 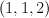 . This is straightforward quantum Lefschetz:
. This is straightforward quantum Lefschetz:
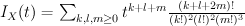
Regularizing this gives period sequence 31:
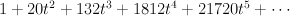
- the blow-up of
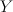 , the 2-to-1 cover of
, the 2-to-1 cover of  with branch locus a divisor of type (2,2), with center a smooth fiber of
with branch locus a divisor of type (2,2), with center a smooth fiber of 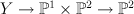 . The variety
. The variety 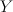 is a hypersurface of type
is a hypersurface of type 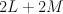 in the rank-2 toric variety with weight data:
in the rank-2 toric variety with weight data:
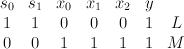
We need to blow up the locus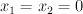 , obtaining our variety
, obtaining our variety  as a hypersurface of type
as a hypersurface of type 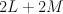 in the toric variety with weight data:
in the toric variety with weight data:
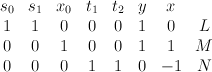
Quantum Lefschetz gives:
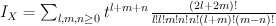
and regularizing gives period sequence 151:
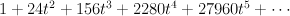
- the blow-up of
 with center a curve of bidegree (5,2) that projects isomorphically to a conic in
with center a curve of bidegree (5,2) that projects isomorphically to a conic in  . We construct this as a codimension-2 complete intersection in
. We construct this as a codimension-2 complete intersection in 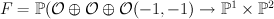 .
.  has weight data:
has weight data:
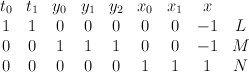
The equations defining are
are
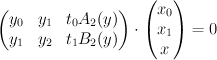
where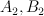 are quadratic polynomials in the
are quadratic polynomials in the 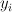 , and so
, and so  is a complete intersection of type
is a complete intersection of type 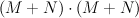 in
in  . Quantum Lefschetz gives:
. Quantum Lefschetz gives:
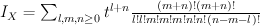
and regularizing gives a period sequence that we do not have yet:
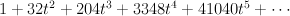
- the blow-up of
 with center the disjoint union of a line
with center the disjoint union of a line  and an elliptic curve
and an elliptic curve  of degree 4. Since
of degree 4. Since  is a (2,2) complete intersection in
is a (2,2) complete intersection in  , our variety
, our variety  is a hypersurface of type
is a hypersurface of type 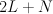 in the toric variety with weight data:
in the toric variety with weight data:

Quantum Lefschetz gives:
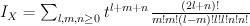
and regularizing gives period sequence 146:
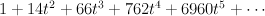
- the blow-up
 of
of 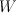 with center an elliptic curve which is a complete intersection of two members of
with center an elliptic curve which is a complete intersection of two members of 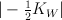 . Recall that
. Recall that 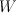 is a (1,1) hypersurface in
is a (1,1) hypersurface in 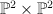 , and so
, and so  is a complete intersection in
is a complete intersection in 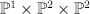 of type
of type 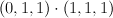 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:
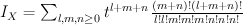
and regularizing gives period sequence 36:
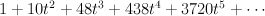
Note that this is a D4 form (i.e. the Picard–Fuchs equation has unexpectedly low degree in D). It is almost certainly a G-Fano, as there is an obvious
 -action.
-action. - a member of the linear system
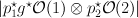 on
on 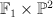 , where
, where 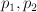 are the projections and
are the projections and  is the blow-up. The weight data for
is the blow-up. The weight data for 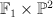 are:
are:
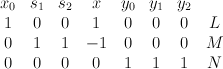
Quantum Lefschetz gives:
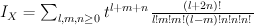
and regularizing gives period sequence 85:
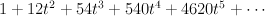
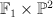 admits an obvious map to
admits an obvious map to 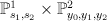 . Writing the equation defining
. Writing the equation defining  in the form
in the form 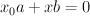 we find that
we find that  is a divisor of type (0,2) and
is a divisor of type (0,2) and 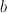 is a divisor of type (1,2). Thus
is a divisor of type (1,2). Thus  is also the blow up of
is also the blow up of  in a curve of bidegree (4,2) that is a complete intersection of type
in a curve of bidegree (4,2) that is a complete intersection of type 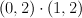 .
. - the blow-up of the cone
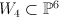 over the Veronese surface
over the Veronese surface 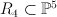 with center the disjoint union of a vertex and a quartic in
with center the disjoint union of a vertex and a quartic in 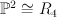 . Thus
. Thus  is a hypersurface of type
is a hypersurface of type 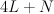 in the toric variety with weight data:
in the toric variety with weight data:
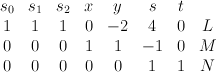
Quantum Lefschetz gives:
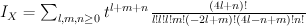
and regularizing gives period sequence 68:
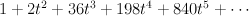
- the blow-up of a quadric
 in
in 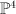 with center a disjoint union of two conics on
with center a disjoint union of two conics on  . We take
. We take  to be the locus
to be the locus 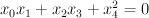 in
in 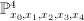 , and take the conics to be cut out of
, and take the conics to be cut out of  by
by 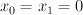 and
and 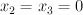 ; note that the intersection of these two planes misses
; note that the intersection of these two planes misses  . So we can construct the variety
. So we can construct the variety  as a hypersurface of type
as a hypersurface of type 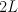 in the toric variety with weight data:
in the toric variety with weight data:
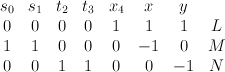
Quantum Lefschetz gives:
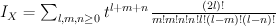
and regularizing gives period sequence 67:
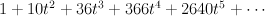
- the blow-up
 of
of  with center a complete intersection of two general members of
with center a complete intersection of two general members of 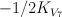 .
.  is also the blow up of
is also the blow up of  in a curve of bidegree (2,3) that is a complete intersection of type
in a curve of bidegree (2,3) that is a complete intersection of type 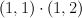 . Consider the toric variety with weight data:
. Consider the toric variety with weight data:
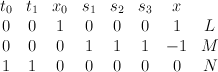
This is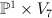 , and
, and  is cut out here as a hypersurface of type
is cut out here as a hypersurface of type 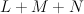 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:
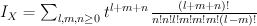
and regularizing gives period sequence 107:
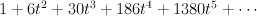
To see that
 is a blow-up of
is a blow-up of  as claimed, note that
as claimed, note that 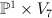 admits an obvious map to
admits an obvious map to 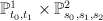 . Rewriting the equation defining
. Rewriting the equation defining  in the form
in the form 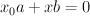 we see that
we see that  is a divisor of type (1,1) and
is a divisor of type (1,1) and 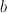 is a divisor of type (1,2). This suffices.
is a divisor of type (1,2). This suffices. - the blow-up of
 with centre a disjoint union of a twisted cubic and a line. As we will see,
with centre a disjoint union of a twisted cubic and a line. As we will see,  is also the blow up of
is also the blow up of  in a curve of bidegree (3,2) that projects isomorphically to a conic in
in a curve of bidegree (3,2) that projects isomorphically to a conic in  . We begin by exhibiting
. We begin by exhibiting  as a complete intersection in a toric variety
as a complete intersection in a toric variety  . The twisted cubic
. The twisted cubic  is cut out of
is cut out of 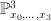 by the equations:
by the equations:
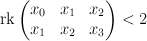
The blow up of along
along  is cut out of
is cut out of 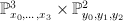 by the equation:
by the equation:
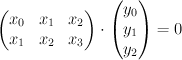
Observe that
 is disjoint from the line
is disjoint from the line 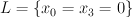 . We therefore blow up
. We therefore blow up 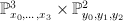 along the locus
along the locus 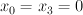 , obtaining the toric variety
, obtaining the toric variety  with weight data:
with weight data:
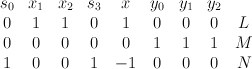
The equations defining inside
inside  are:
are:
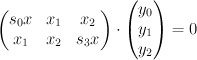
and so is a complete intersection of type
is a complete intersection of type 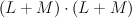 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:

and regularizing gives period sequence 144:
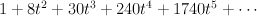
To see that
 is a blow-up of
is a blow-up of  as claimed, note that the map
as claimed, note that the map 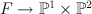 is
is ![[x_0:x_1:x_2:s_3:x:y_0:y_1:y_2] \mapsto [s_0:s_3:y_0:y_1:y_2] [x_0:x_1:x_2:s_3:x:y_0:y_1:y_2] \mapsto [s_0:s_3:y_0:y_1:y_2]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/aa1/aa1b218e22d2b7dae1117acf91cd2f2c-ffffff-000000-0.png) . Rewriting the equations of
. Rewriting the equations of  as:
as: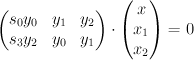
we see that is the blow-up of
is the blow-up of  along the curve
along the curve 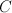 given by:
given by:
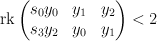
The equations defining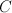 are:
are:
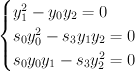
and so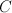 lies entirely within the “cylinder surface”
lies entirely within the “cylinder surface” 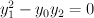 . This cylinder surface is abstractly isomorphic to
. This cylinder surface is abstractly isomorphic to 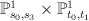 , where
, where 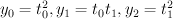 . The equations of
. The equations of 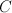 become:
become:
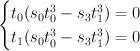
Thus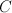 is as described above.
is as described above. - the blow-up…
- the blow-up of
 with center the union of a cubic in a plane
with center the union of a cubic in a plane 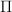 and a point
and a point  not in
not in  . Let
. Let  be
be 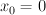 in
in  , and let
, and let  be
be 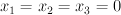 . Thus
. Thus  is the blow-up of the curve
is the blow-up of the curve 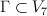 given by:
given by:
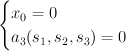
where the blow-up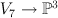 is
is ![[x_0:s_1:s_2:s_3:x] \mapsto [x_0:s_1 x: s_2 x: s_3 x] [x_0:s_1:s_2:s_3:x] \mapsto [x_0:s_1 x: s_2 x: s_3 x]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/c06/c0619d92b3eca98aa2358444f3d1baad-ffffff-000000-0.png) . Thus
. Thus  is a hypersurface of type
is a hypersurface of type 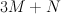 in the toric variety with weight data:
in the toric variety with weight data:
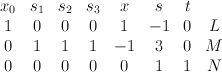
Quantum Lefschetz gives:
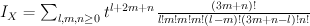
and regularizing gives period sequence 148:
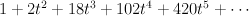
- the blow-up
 of a quadric
of a quadric 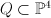 with center the disjoint union of a line on
with center the disjoint union of a line on  and a conic on
and a conic on  .
.  is the blow-up of
is the blow-up of  along a curve of bidegree (2,2) that is a complete intersection of type
along a curve of bidegree (2,2) that is a complete intersection of type 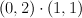 . To see this, we first exhibit
. To see this, we first exhibit  as a hypersurface in a toric variety. Note that the blow-up of
as a hypersurface in a toric variety. Note that the blow-up of 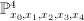 along the plane
along the plane 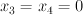 and the line
and the line 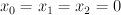 is toric with weight data:
is toric with weight data:
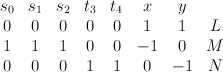
The map to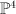 here sends
here sends ![[s_0 : s_1 : s_2 : t_3 : t_4 : x : y] \mapsto [s_0 x : s_1 x : s_2 x : t_3 y : t_4 y] [s_0 : s_1 : s_2 : t_3 : t_4 : x : y] \mapsto [s_0 x : s_1 x : s_2 x : t_3 y : t_4 y]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/a7e/a7e1e85b5ec637f22489836d1b6be574-ffffff-000000-0.png) ; there is also a map to
; there is also a map to  given by
given by ![[t_0 : t_1 : s_0 : s_1 : s_2] [t_0 : t_1 : s_0 : s_1 : s_2]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/0f3/0f3c54ee1a2b00b74e94dad225cd5efd-ffffff-000000-0.png) .
.  is cut out of the above toric variety by a section of
is cut out of the above toric variety by a section of 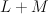 . Thus we have:
. Thus we have:

and regularizing gives period sequence 112:
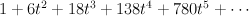
To see that is the blow-up of
is the blow-up of  as claimed, write the equation defining
as claimed, write the equation defining  as
as  . Then by homogeneity
. Then by homogeneity  is a section of (0,2) and
is a section of (0,2) and 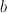 is a section of (1,1).
is a section of (1,1). - the blow-up of
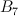 with center the strict transform of a twisted cubic through the blown-up point
with center the strict transform of a twisted cubic through the blown-up point 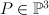 . Let
. Let  be the point
be the point 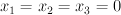 in
in  , and let
, and let  be the curve given by
be the curve given by
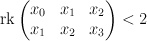
Let the blow-up be given by
be given by ![[x_0 : s_ 1 : s_2 : s_3 : x] \mapsto [x_0 : s_1 x: s_2 x: s_3 x] [x_0 : s_ 1 : s_2 : s_3 : x] \mapsto [x_0 : s_1 x: s_2 x: s_3 x]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/975/975afb11eaaf478eb7c1c8f921af1d4f-ffffff-000000-0.png) . Then the strict transform of
. Then the strict transform of  in
in  is given by:
is given by:
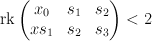
As before, we introduce new variables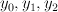 and the toric variety
and the toric variety  with weight data:
with weight data:

 is cut out by the equations:
is cut out by the equations:
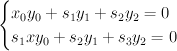
Quantum Lefschetz gives:

and regularizing gives period sequence 119:
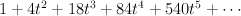
- a smooth divisor on
 of tridegree
of tridegree 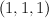 . This is straightforward quantum Lefschetz:
. This is straightforward quantum Lefschetz:
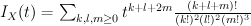
Regularizing this gives period sequence 37:
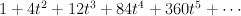
Note that is also the blow-up of
is also the blow-up of  along a curve of bidegree (1,2).
along a curve of bidegree (1,2). - the blow-up of
 with center a disjoint union of a line
with center a disjoint union of a line  and a conic. Take the line to be
and a conic. Take the line to be 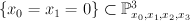 , and take the conic to be
, and take the conic to be 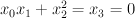 . The blow-up of
. The blow-up of  in
in  is
is ![[s_0 : s_1 : x : x_2 : x_3] \mapsto [s_0 x : s_1 x : x_2 : x_3] [s_0 : s_1 : x : x_2 : x_3] \mapsto [s_0 x : s_1 x : x_2 : x_3]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/1c5/1c5ab10eeb7194deeaca6f79d6f3e14e-ffffff-000000-0.png) , and the strict transform of the conic is cut out by
, and the strict transform of the conic is cut out by 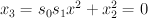 . Thus
. Thus  is a hypersurface of type
is a hypersurface of type 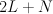 in the toric variety with weight data:
in the toric variety with weight data:
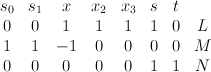
cut out by the equation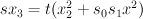 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:
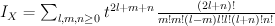
and regularizing gives period sequence 160:
- the blow-up of a quadric
 with center two non-colinear points. We construct this by taking the equation of the quadric to be
with center two non-colinear points. We construct this by taking the equation of the quadric to be 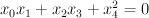 inside
inside 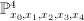 , blowing up the line
, blowing up the line 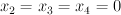 in
in 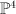 (this line is not contained in
(this line is not contained in  ) and then taking the proper transform of the quadric inside the blow-up of
) and then taking the proper transform of the quadric inside the blow-up of 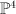 . This is a hypersurface of type
. This is a hypersurface of type 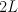 in the toric variety with weight data
in the toric variety with weight data
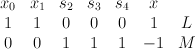
Quantum Lefschetz gives:
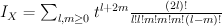
and regularizing gives period sequence 57:
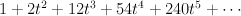
- the blow-up of a 3-dimensional quadric
 with center two disjoint lines on it. We take the quadric with equation
with center two disjoint lines on it. We take the quadric with equation 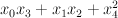 in
in 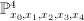 and blow up the lines
and blow up the lines 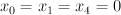 and
and 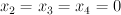 . Thus
. Thus  is a hypersurface of type
is a hypersurface of type 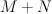 in the toric variety with weight data:
in the toric variety with weight data:
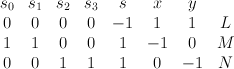
Quantum Lefschetz gives:

and regularizing gives period sequence 63:
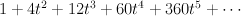
- the blow-up of
 along a curve of bidegree (2,1).
along a curve of bidegree (2,1).  is described by a single equation
is described by a single equation 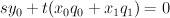 , where
, where 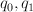 are quadratic polynomials in
are quadratic polynomials in 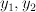 , in the toric variety with weight data
, in the toric variety with weight data

Quantum Lefschetz gives:
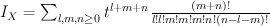
and regularizing gives period sequence 98:
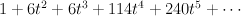
- the blow-up of
 along a curve of bidegree (0,2), that is a conic in
along a curve of bidegree (0,2), that is a conic in 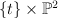 . Thus
. Thus  is described by a single equation
is described by a single equation 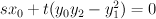 in the toric variety with weight data
in the toric variety with weight data
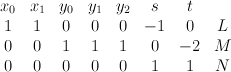
Quantum Lefschetz gives:
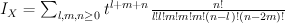
and regularizing gives period sequence 152:
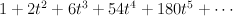
- the blow-up of
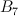 with center a conic passing through the blown-up point
with center a conic passing through the blown-up point 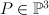 . Let
. Let 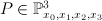 be the point
be the point 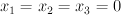 . Define the conic by:
. Define the conic by:
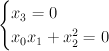
Taking the proper transform under the blow-up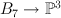 gives the equations:
gives the equations:
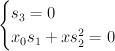
where the blow-up is![[x_0 : s_1 : s_2 : s_3 : x] \mapsto [x_0 : x s_1 : x s_2 : x s_3] [x_0 : s_1 : s_2 : s_3 : x] \mapsto [x_0 : x s_1 : x s_2 : x s_3]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/bee/beed813a435c77c1493a625f04e66879-ffffff-000000-0.png) , and so we need to consider the locus:
, and so we need to consider the locus:
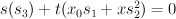
This is a hypersurface of type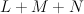 in the toric variety with weight data:
in the toric variety with weight data:
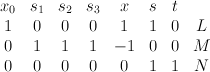
Quantum Lefschetz gives:
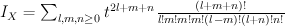
and regularizing gives period sequence 158:
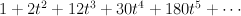
- the fiber product
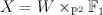 where
where 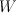 is a (1,1) hypersurface in
is a (1,1) hypersurface in 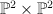 . This is the blow up of
. This is the blow up of  along a curve of bidegree (1,1). To see this, note first that
along a curve of bidegree (1,1). To see this, note first that  is cut out of
is cut out of 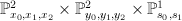 by the equations:
by the equations:
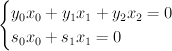
The first equation here cuts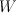 out of
out of 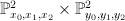 ; the second equation cuts
; the second equation cuts 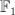 out of
out of 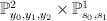 , as it is the equation defining the blow-up of
, as it is the equation defining the blow-up of  .
.
We now exhibit
 as the blow-up of a curve in
as the blow-up of a curve in  by projecting to
by projecting to 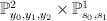 . This projection is an isomorphism away from the locus where the matrix
. This projection is an isomorphism away from the locus where the matrix
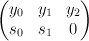
drops rank. This locus is:
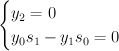
i.e. a curve in of bidegree (1,1).
of bidegree (1,1).
We can further simplify things by writing as a hypersurface in
as a hypersurface in 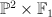 . Write the co-ordinates on
. Write the co-ordinates on 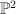 as
as 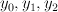 and the co-ordinates on
and the co-ordinates on 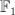 as
as 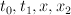 ; here the blow-up
; here the blow-up 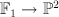 sends
sends ![[t_0 : t_1 : x : x_2] \mapsto [t_0 x : t_1 x : x_2] [t_0 : t_1 : x : x_2] \mapsto [t_0 x : t_1 x : x_2]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/d71/d71073407ea9e49bf5725832d8a16bc8-ffffff-000000-0.png) .The two equations defining
.The two equations defining  (given above) reduce to the single equation:
(given above) reduce to the single equation:
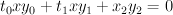
Thus is a hypersurface of type
is a hypersurface of type 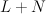 in the toric variety with weight data:
in the toric variety with weight data:
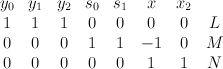
Quantum Lefschetz gives:
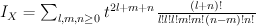
and regularizing gives period sequence 86:
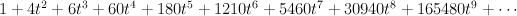
- the blow-up of
 with center two disjoint lines. This is the toric variety with weight data:
with center two disjoint lines. This is the toric variety with weight data:
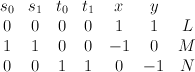
The blow-up map is![[s_0 : s_1 : t_0 : t_1 : x : y] \mapsto [s_0 x : s_1 x : t_0 y : t_1 y ] [s_0 : s_1 : t_0 : t_1 : x : y] \mapsto [s_0 x : s_1 x : t_0 y : t_1 y ]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/0ae/0aeb2105340c09ea5aabd805603582d4-ffffff-000000-0.png) . We have:
. We have:
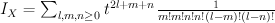
and regularizing gives period sequence 41:
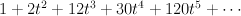
- the blow-up
 of
of  with center a disjoint union of a point and a line. This is also the blow-up of
with center a disjoint union of a point and a line. This is also the blow-up of  in a curve of bidegree (0,1). So
in a curve of bidegree (0,1). So  is a toric variety, with weight data:
is a toric variety, with weight data:
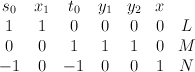
The blow-up map is![[s_0 : x : t_0 : y_1 : y_2 : x] \mapsto [s_0 x : x_1 : t_0 x : y_1 : y_2] [s_0 : x : t_0 : y_1 : y_2 : x] \mapsto [s_0 x : x_1 : t_0 x : y_1 : y_2]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/3b4/3b41e56a099040bcde86f72dd1c7d03e-ffffff-000000-0.png) . We have:
. We have:
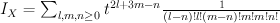
and regularizing gives period sequence 113:

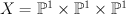 . This gives:
. This gives:
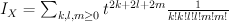
and regularizing gives period sequence 21:
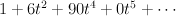
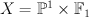 . This gives:
. This gives:
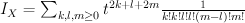
and regularizing gives period sequence 90:
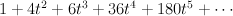
- the blow-up of
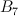 with center a line on the exceptional divisor of the blow-up
with center a line on the exceptional divisor of the blow-up 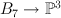 . This is a toric variety with weight data:
. This is a toric variety with weight data:
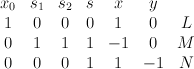
We have:
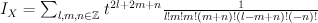
and regularizing gives period sequence 163:
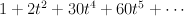
- the blow-up of
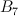 with center the strict transform of a line through the blown-up point
with center the strict transform of a line through the blown-up point 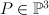 . This is a toric variety with weight data:
. This is a toric variety with weight data:
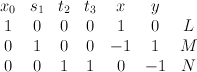
We have:
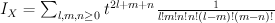
and regularizing gives period sequence 84:
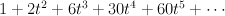
- the total space of the bundle
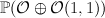 over
over 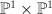 . This is the toric variety with weight data:
. This is the toric variety with weight data:
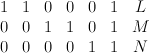
We have:
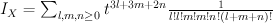
and regularizing gives period sequence 53:
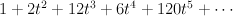
Note
Consider the hypersurface of type 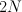 in the toric variety with weight data:
in the toric variety with weight data:
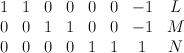
We have:
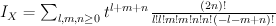
and regularizing gives period sequence 32:
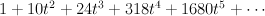
It seems that Mori-Mukai may have missed this variety, and have included number 2 in the rank 3 list by mistake. Note that our  is a section of
is a section of 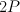 where
where  is the tautological bundle on
is the tautological bundle on 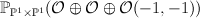 . The degree of
. The degree of  is 28.
is 28.
Never mind: this is #2 on the Mori-Mukai list of rank-4 Fanos.
On 25, 29, 30 and 31: these are smooth toric varieties.
They correspond to period sequences 41, 53, 84 and 163.
To be more precise:
25 is unique smooth toric Fano with P=3 and degree 44,
it corresponds to period sequence 41.
31 is unique smooth toric Fano with P=3 and degree 52,
it corresponds to period sequence 53.
29 and 30 has same degree 50 and correspond to p.s. 84 (grdb – 520136) and 163 (grdb – 520127).
Need an extra computation to separate these two.
Here is it.
Mirror of is
is 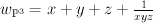
2.29 is blowup of line on exceptional divisor, so its mirror is
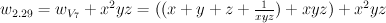
This Laurent polynomial has period sequence 163
[1, 0, 2, 0, 30, 60, 380, 840, 5950, 22680]
2.30 is blowup of line that strict transform of line passing the center of blowup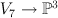 ,
,
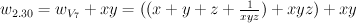
so its mirror is
This Laurent polynomial has period sequence 84
[1, 0, 2, 6, 30, 60, 470, 1680, 7630, 34440]
[Sorry, I had a typo here (!), 84 is correct]
Also, for 2.25 mirror is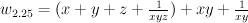
On 3.7
It is not a G-Fano, but has a little of symmetry (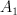 ), so it looks like
), so it looks like
Fano with Picard number 2.
(According to Matsuki’s data) other Fanos with this property in this list should have the following numbers:
3, 9, 10, 17, 19, 20, 25, 31
I wrote a wider review of these issues in the post
expected distribution of equations
—-
Also I propose not to call this type of equation D4, since D4 is already reserved for equations that look like RQDE of P^4 (or 4-dimensional quadric). Better name for RQDE
of general Fano 3-fold with Picard number 2 is D3+1.
In general, type of RQDE for generic Fano variety is classified by its Lefschetz decomposition i.e. partition or Young tableux.
For Fano threefolds we will probably have just D3, D3+1, D3+2 and four D3+3’s.
(3+2 is a nickname for 3+2×1,
3+3 is a nickname for 3+3×1).
On 6, 10 and 23.
3.6 has period sequence 146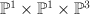 .
.
It is represented by complete intersection of degrees (1,0,2) and (0,1,1) in
3.10 has period sequence 67.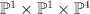 .
.
It is represented by complete intersection of degrees (1,0,1), (0,1,1) and (0,0,2) in
3.23 has period sequence 86.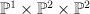 .
.
It is represented by complete intersection of degrees (1,1,0) and (0,1,1) in
On 3.2: its description basically says it is a divisor in smooth toric fourfold.
On 3.24:
there is a typo in the very end (!)
the period is _not_ ps[130]: [1, 0, 4, 6, 60, 180, 1210, 5040, 30940, 150360]
but ps[86]: [1, 0, 4, 6, 60, 180, 1210, 5460, 30940, 165480]
They have same first 7 entries, so it was easy to mistake.
Moreover, period sequence 130 is bad – it has (2D-1) as a multiple. So this resolves the ambiguity we had before.
Also – 3.24 has 3 terminal Gorenstein degenerations,
and TGTD ansatz applied to them is exactly ps[86].
3.24 corresponds to ps[86]
3.23 should correspond to ps[158]
And there will be exactly 1-1 correspondence between 98 Fano threefolds and 98 good period sequences.
Following is the computation of first 10 terms:
Moreover, the description for 3.24 seems too complicated.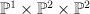 we can already apply quantum Lefschetz:
we can already apply quantum Lefschetz:
After on the third line X is described as the complete intersection of degrees (1,1,0) and (0,1,1) in
regularizing and normalizing we get
i.e. period sequence 86.