Rank 2 Fano 3-folds
We compute the quantum period sequences of Fano 3-folds in the Mori-Mukai list.
- [Not very Fano]The blow-up of
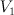 with centre an elliptic curve which is the intersection of two members of
with centre an elliptic curve which is the intersection of two members of 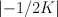 . This is a hypersurface in a toric variety
. This is a hypersurface in a toric variety  . The divisor diagram for
. The divisor diagram for  is
is 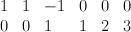 .
.
Note that is a scroll over
is a scroll over 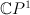 with fibre
with fibre 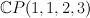 . There is a morphism
. There is a morphism 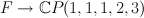 , which is the blow up along
, which is the blow up along  ; this map sends
; this map sends ![[s_0,s_1,x, x_2, y, z] [s_0,s_1,x, x_2, y, z]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/f00/f00f86106d08063f0ac225f02a494414-ffffff-000000-0.png) to
to ![[s_0x,s_1x,x_2,y,z] [s_0x,s_1x,x_2,y,z]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/679/67955408a9b33de8e1dcb8cfbe711c3b-ffffff-000000-0.png) . There are two line bundles
. There are two line bundles 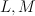 on
on  :
:  are section of
are section of  ;
; 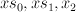 are sections of
are sections of  ;
; 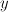 is a section of
is a section of 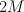 and
and  of
of 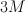 .
.  is cut out by a section of
is cut out by a section of 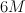 : we have
: we have 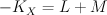 .
.
Applying quantum Lefschetz gives:
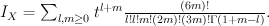
Regularizing this (that is, pre-multiplying by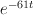 so as to kill the linear term in
so as to kill the linear term in 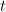 , and then replacing
, and then replacing 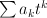 by
by 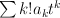 ) gives a period sequence that is not in our list:
) gives a period sequence that is not in our list:
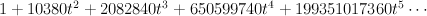
Note that there are two birational models of the ambient space here, corresponding to the two chambers in the divisor diagram. But the sum defining the I-function really takes place over the intersection of the Mori cones of the two birational models, because of the factor of
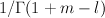 in the summand. This factor vanishes outside one of the Kahler cones; similarly
in the summand. This factor vanishes outside one of the Kahler cones; similarly 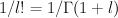 vanishes outside the other Kahler cone. Similar things happen in many of the examples below.
vanishes outside the other Kahler cone. Similar things happen in many of the examples below. - [Not very Fano]The double cover of
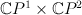 branched along a divisor of bidegree
branched along a divisor of bidegree 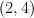 . This is a hypersurface in a toric variety
. This is a hypersurface in a toric variety  with divisor diagram
with divisor diagram  . With coordinates
. With coordinates 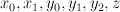 , the defining equation of
, the defining equation of  is
is 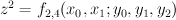 . Denote by
. Denote by  the line bundle with sections
the line bundle with sections 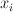 and by
and by  the line bundle with sections
the line bundle with sections 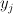 ; then
; then  .Quantum Lefschetz gives
.Quantum Lefschetz gives
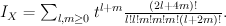
Regularizing this gives a period sequence that is not in our list:
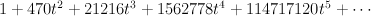
- [Not very Fano]the blow up of
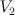 with centre an elliptic curve which is the intersection of two elements of
with centre an elliptic curve which is the intersection of two elements of 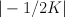 . This is a hypersurface in a toric variety
. This is a hypersurface in a toric variety  . The divisor diagram for
. The divisor diagram for  is
is 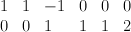 .
.
Note that is a scroll over
is a scroll over 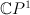 with fibre
with fibre 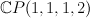 . There is a morphism
. There is a morphism 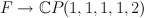 , which is the blow up along
, which is the blow up along  ; this map sends
; this map sends ![[s_0,s_1,x, x_2, x_3, y] [s_0,s_1,x, x_2, x_3, y]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/8f9/8f95af3f020c01b72e0f8d5c8c79aa4a-ffffff-000000-0.png) to
to ![[s_0x,s_1x,x_2,x_3,y] [s_0x,s_1x,x_2,x_3,y]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/ce1/ce1bc3a1db3b00e2ff93fcae7fb68443-ffffff-000000-0.png) . There are two line bundles
. There are two line bundles 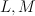 on
on  :
:  are section of
are section of  ;
; 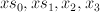 are sections of
are sections of  ;
; 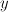 is a section of
is a section of 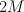 .
.  is cut out by a section of
is cut out by a section of 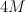 : we have
: we have 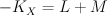 . Quantum Lefschetz gives
. Quantum Lefschetz gives
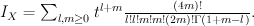
Regularizing this gives a period sequence that is not in our list:

- the blow up of
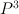 with centre an intersection of two cubics. Thus,
with centre an intersection of two cubics. Thus,  is a divisor of bidegree
is a divisor of bidegree 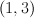 on
on 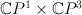 . We denote by
. We denote by  and
and  the pull backs of the tautological bundles on the two factors. We have
the pull backs of the tautological bundles on the two factors. We have 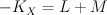 , and quantum Lefschetz gives:
, and quantum Lefschetz gives:
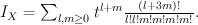
Regularizing this gives period sequence 49:
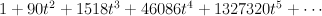
- the blow up of
 with centre a plane cubic.This is a hypersurface in a toric variety
with centre a plane cubic.This is a hypersurface in a toric variety  . The divisor diagram for
. The divisor diagram for  is
is 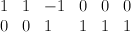 .
.
Note that is a scroll over
is a scroll over  with fibre
with fibre 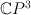 . There is a morphism
. There is a morphism 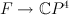 , which is the blow up along
, which is the blow up along  ; this map sends
; this map sends ![[s_0,s_1,x, x_2, x_3, x_4] [s_0,s_1,x, x_2, x_3, x_4]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/eb6/eb6f927c04cfebb0603c927cbcebfc93-ffffff-000000-0.png) to
to ![[s_0x,s_1x,x_2,x_3,x_4] [s_0x,s_1x,x_2,x_3,x_4]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/952/952d8af5ba71df89c50c3d554517b4f7-ffffff-000000-0.png) . There are two line bundles
. There are two line bundles 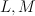 on
on  :
:  are section of
are section of  ;
; 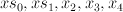 are sections of
are sections of  .
.  is cut out by a section of
is cut out by a section of 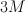 : we have
: we have 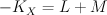 .Quantum Lefschetz gives
.Quantum Lefschetz gives
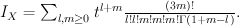
Regularizing this gives period sequence 34:
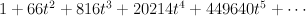 .
. - a divisor of bidegree
 in
in 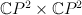 . Quantum Lefschetz gives
. Quantum Lefschetz gives
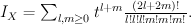
Regularizing this gives period sequence 11:
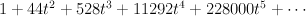 .
.
Note that this is a D3 form: even though the Fano has rank 2, the quantum cohomology D-module splits off a “rank 1” irreducible piece (i.e. a piece of dimension 4, which is the size of the cohomology of a rank-1 Fano 3-fold).
has rank 2, the quantum cohomology D-module splits off a “rank 1” irreducible piece (i.e. a piece of dimension 4, which is the size of the cohomology of a rank-1 Fano 3-fold). - the blow up of a quadric
 with centre the intersection of two members of
with centre the intersection of two members of 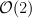 . Thus,
. Thus,  is the complete intersection of two divisors in
is the complete intersection of two divisors in 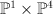 , of bidegrees
, of bidegrees 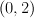 and
and 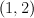 . We denote by
. We denote by  and
and  the pull backs of the tautological bundles on the two factors. We have
the pull backs of the tautological bundles on the two factors. We have 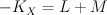 , and quantum Lefschetz gives:
, and quantum Lefschetz gives:
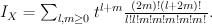
Regularizing this gives period sequence 51:
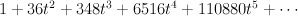
- a double cover of
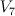 with branch locus a member
with branch locus a member 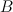 of
of 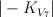 such that
such that 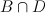 is smooth, where
is smooth, where 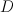 is the exceptional divisor of the blow-up
is the exceptional divisor of the blow-up 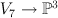 . This is a hypersurface in a toric variety
. This is a hypersurface in a toric variety  . The divisor diagram for
. The divisor diagram for  is
is 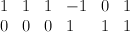 . Call the co-ordinates
. Call the co-ordinates 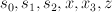 . Let
. Let  be the line bundle with sections
be the line bundle with sections 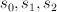 and let
and let  be the line bundle with sections
be the line bundle with sections 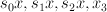 ;
;  is a section of
is a section of 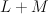 . The variety
. The variety  is a section of
is a section of 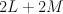 on
on  ; we have
; we have 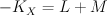 .Quantum Lefschetz gives:
.Quantum Lefschetz gives:
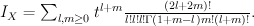
Regularizing this gives period sequence 26:
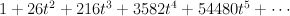
- the blow up of
 in a curve
in a curve  of degree 7 and genus 5.
of degree 7 and genus 5.  is cut by the equations:
is cut by the equations:
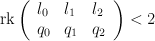
where the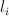 are linear forms and the
are linear forms and the 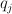 are quadratics. Let
are quadratics. Let 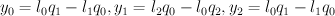 . The relations (szyzgies) between these equations are generated by:
. The relations (szyzgies) between these equations are generated by:
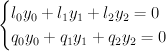
Thus is given by these two equations in
is given by these two equations in  , where the first factor has co-ordinates
, where the first factor has co-ordinates 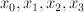 and the second factor has co-ordinates
and the second factor has co-ordinates 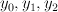 . In other words,
. In other words,  is a complete intersection in
is a complete intersection in  of type
of type  ; we have
; we have 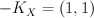 .
.
Quantum Lefschetz gives:
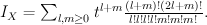
Regularizing this gives period sequence 62:
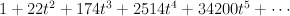
- the blow up of
 with centre an elliptic curve which is the intersection of two hyperplane sections. This is a complete intersection in a toric variety
with centre an elliptic curve which is the intersection of two hyperplane sections. This is a complete intersection in a toric variety  . The divisor diagram for
. The divisor diagram for  is
is 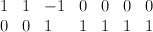 .
.
Note that is a scroll over
is a scroll over  with fibre
with fibre  . There is a morphism
. There is a morphism  , which is the blow up along
, which is the blow up along  ; this map sends
; this map sends ![[s_0,s_1,x, x_2, x_3, x_4,x_5] [s_0,s_1,x, x_2, x_3, x_4,x_5]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/dfa/dfa5ff7d3b45f6a533618a59199cf48c-ffffff-000000-0.png) to
to ![[s_0x,s_1x,x_2,x_3,x_4,x_5] [s_0x,s_1x,x_2,x_3,x_4,x_5]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/5f7/5f7c0c52609a8fad1441e79f143c767f-ffffff-000000-0.png) . There are two line bundles
. There are two line bundles 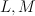 on
on  :
:  are section of
are section of  ;
; 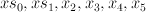 are sections of
are sections of  .
.  is a complete intersection of divisors
is a complete intersection of divisors 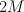 and
and 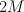 in
in  ; we have
; we have 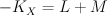 . Quantum Lefschetz gives
. Quantum Lefschetz gives
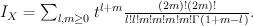
Regularizing this gives period sequence 40:
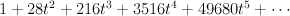
- the blow up of
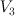 with centre a line on it. This is a hypersurface in a toric variety
with centre a line on it. This is a hypersurface in a toric variety  . The divisor diagram for
. The divisor diagram for  is
is 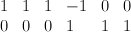 .
.
Note that is a scroll over
is a scroll over  with fibre
with fibre 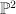 . There is a morphism
. There is a morphism 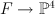 , which is the blow up along
, which is the blow up along 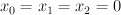 ; this map sends
; this map sends ![[s_0,s_1,s_2, x, x_3, x_4] [s_0,s_1,s_2, x, x_3, x_4]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/9f0/9f0e05d81d5949df0e3d8a70e66e14d8-ffffff-000000-0.png) to
to ![[s_0x,s_1x,s_2x,x_3,x_4] [s_0x,s_1x,s_2x,x_3,x_4]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/a14/a146ca7736b172e89094234bad7f6033-ffffff-000000-0.png) . There are two line bundles
. There are two line bundles 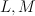 on
on  :
:  are section of
are section of  ;
; 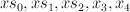 are sections of
are sections of 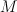 .
.  is cut out by a section of
is cut out by a section of 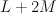 in
in  ; we have
; we have 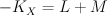 . Quantum Lefschetz gives
. Quantum Lefschetz gives
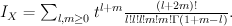
Regularizing this gives period sequence 56:
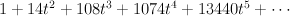
- the blow up of
 in a curve
in a curve  of degree 6 and genus 3.
of degree 6 and genus 3.  is cut by the equations:
is cut by the equations:
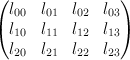
where the are linear forms. Let
are linear forms. Let 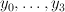 be the
be the 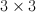 minors. The relations (szyzgies) between these equations are generated by:
minors. The relations (szyzgies) between these equations are generated by:
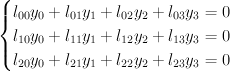
Thus is given by these three equations in
is given by these three equations in 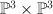 , where the first factor has co-ordinates
, where the first factor has co-ordinates 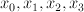 and the second factor has co-ordinates
and the second factor has co-ordinates 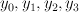 . In other words,
. In other words,  is a complete intersection in
is a complete intersection in 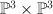 of type
of type 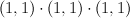 ; we have
; we have 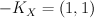 .
.
Quantum Lefschetz gives:
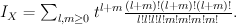
Regularizing this gives period sequence 13:

which is a D3 form (because this is obviously a G-Fano: it is Galkin’s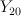 ).
). - the blow-up of a 3-dimensional quadric
 in a curve
in a curve  of genus 2 and degree 6. This is a complete intersection in a toric variety. We have
of genus 2 and degree 6. This is a complete intersection in a toric variety. We have 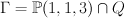 where the embedding
where the embedding 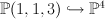 sends
sends ![[s_0:s_1:y] \in \PP(1,1,3) [s_0:s_1:y] \in \PP(1,1,3)](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/505/50543ab3dc7020f9a38bfef7928acf9b-ffffff-000000-0.png) to
to ![[s_0^3:s_0^2 s_1:s_0 s_1^2:s_1^3:y] \in \PP^4 [s_0^3:s_0^2 s_1:s_0 s_1^2:s_1^3:y] \in \PP^4](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/e12/e1292058226570391265bafa0fb33b12-ffffff-000000-0.png) . We blow up
. We blow up  inside
inside  . The equations defining
. The equations defining  are
are
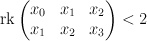
where![[x_0:x_1:x_2:x_3:x_4] [x_0:x_1:x_2:x_3:x_4]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/141/141d5611ff24094986e9f4a39be17a3d-ffffff-000000-0.png) are co-ordinates on
are co-ordinates on  . The blown-up variety
. The blown-up variety  is the complete intersection in
is the complete intersection in 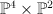 cut out by the equations:
cut out by the equations:
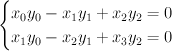
where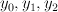 are co-ordinates on
are co-ordinates on  . Our Fano
. Our Fano  is the complete intersection of
is the complete intersection of  with a quadric
with a quadric 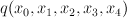 . Thus
. Thus  is a complete intersection of type
is a complete intersection of type 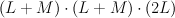 in
in 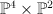 ; here
; here  is the tautological bundle on
is the tautological bundle on 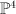 and
and  is the tautological bundle on
is the tautological bundle on  .
.
We have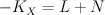 and Quantum Lefschetz gives:
and Quantum Lefschetz gives:
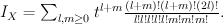
Regularizing this gives period sequence 52:
- the blow-up…
- the blow-up of
 with center the intersection of a quadric and a cubic. This is a hypersurface in a scroll
with center the intersection of a quadric and a cubic. This is a hypersurface in a scroll  . The divisor diagram for
. The divisor diagram for  is
is
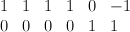 .
.
The projection sends
sends ![[x_0,x_1,x_2, x_3, s, t] [x_0,x_1,x_2, x_3, s, t]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/32c/32cc4c5f9c04acf45aa531cdf00b9e0b-ffffff-000000-0.png) to
to ![[x_0,x_1,x_2,x_3] [x_0,x_1,x_2,x_3]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/7f8/7f8e64ecbcd1e79ff1188de92e9708d6-ffffff-000000-0.png) . There are two line bundles
. There are two line bundles 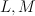 on
on  :
: 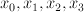 are section of
are section of  ;
; 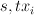 are sections of
are sections of 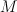 .
.  is cut out of
is cut out of  by a section of
by a section of  ; we have
; we have 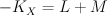 . Quantum Lefschetz gives
. Quantum Lefschetz gives
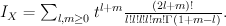
Regularizing this gives period sequence 35:
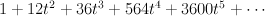
- the blow-up of
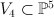 with center a conic on it. This is a complete intersection in a toric variety. We give full details of the construction, as it is a model for several other examples (being a blow-up of a projective hypersurface with center a complete intersection in the ambient projective space).We begin by constructing the blow-up
with center a conic on it. This is a complete intersection in a toric variety. We give full details of the construction, as it is a model for several other examples (being a blow-up of a projective hypersurface with center a complete intersection in the ambient projective space).We begin by constructing the blow-up  of
of  with center the conic
with center the conic 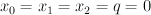 where
where 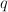 is a quadratic polynomial in
is a quadratic polynomial in 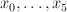 . To do this, introduce new co-ordinates
. To do this, introduce new co-ordinates 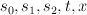 and impose the relation:
and impose the relation:

Thus we construct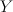 as a hypersurface in the toric variety
as a hypersurface in the toric variety  with divisor diagram
with divisor diagram 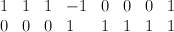 . The co-ordinates on
. The co-ordinates on  here are
here are 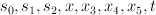 ; the equation defining
; the equation defining  is
is 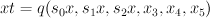 . The map from
. The map from 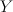 to
to 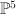 sends
sends ![[s_0,s_1,s_2,x,x_3,x_4,x_5] [s_0,s_1,s_2,x,x_3,x_4,x_5]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/493/4938ce518bdc5d2d04f686f3204219c6-ffffff-000000-0.png) to
to ![[s_0 x, s_1 x, s_2 x, x_3, x_4, x_5] [s_0 x, s_1 x, s_2 x, x_3, x_4, x_5]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/a15/a154983a4b16adaf02f4ab8e39d1c38b-ffffff-000000-0.png) . It is easy to check that this is the blow-up of
. It is easy to check that this is the blow-up of 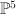 in the conic
in the conic  . Introduce line bundles
. Introduce line bundles  such that
such that 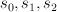 are sections of
are sections of  and
and 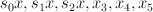 are sections of
are sections of  ; note that
; note that 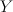 is cut out of
is cut out of  by a section of
by a section of 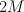 . The Fano
. The Fano  is a complete intersection of 3 divisors
is a complete intersection of 3 divisors 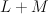 ,
, 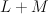 , and
, and 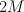 on
on  . We have
. We have 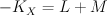 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:
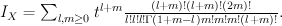
Regularizing this gives period sequence 59:
- the blow-up…
- the double cover of
 with branch locus a divisor of bidegree
with branch locus a divisor of bidegree  . This is a hypersurface in a toric variety
. This is a hypersurface in a toric variety  with divisor diagram
with divisor diagram  . With coordinates
. With coordinates  , the defining equation of
, the defining equation of  is
is 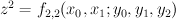 . Denote by
. Denote by  the line bundle with sections
the line bundle with sections 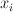 and by
and by  the line bundle with sections
the line bundle with sections 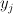 ; then
; then 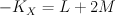 .Quantum Lefschetz gives
.Quantum Lefschetz gives
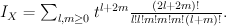
Regularizing this gives period sequence 60:
- the blow-up of
 with center a line on it. We proceed as in example 16;
with center a line on it. We proceed as in example 16;  here is a complete intersection in the toric variety
here is a complete intersection in the toric variety  with divisor diagram
with divisor diagram

The co-ordinates on here are
here are 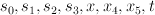 ; the map from
; the map from 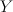 to
to 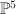 sends
sends ![[s_0,s_1,s_2,s_3,x,x_4,x_5] [s_0,s_1,s_2,s_3,x,x_4,x_5]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/925/925325f4a31e3938542cffcb04b39a8a-ffffff-000000-0.png) to
to ![[s_0 x, s_1 x, s_2 x, s_3 x, x_4, x_5] [s_0 x, s_1 x, s_2 x, s_3 x, x_4, x_5]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/2a3/2a3e02f74e1d811475cbb42df83cd75b-ffffff-000000-0.png) . Introduce line bundles
. Introduce line bundles 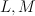 such that
such that 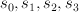 are sections of
are sections of  and
and 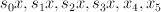 are sections of
are sections of  . Then
. Then  is a complete intersection of 2 divisors
is a complete intersection of 2 divisors 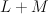 ,
, 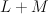 on
on  . We have
. We have 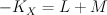 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:

Regularizing this gives period sequence 55:
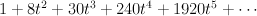
- the blow-up…
- the blow-up…
- the blow-up…
- the blow-up of a quadric with center an intersection of
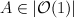 and
and 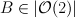 .
.  is a complete intersection of type
is a complete intersection of type  in the toric variety with weight data
in the toric variety with weight data  . We have
. We have 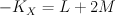 .Quantum Lefschetz gives:
.Quantum Lefschetz gives:
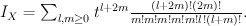
Regularizing this gives period sequence 29:

- A divisor of bidegree
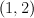 on
on 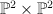 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:
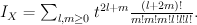
Regularizing this gives period sequence 66:
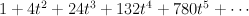
- The blow up of
 with centre an elliptic curve which is the complete intersection of two quadrics.
with centre an elliptic curve which is the complete intersection of two quadrics.  is a divisor of bidegree
is a divisor of bidegree 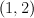 in
in 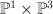 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:
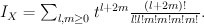
Regularizing this gives period sequence 28:
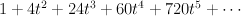
- the blow up…
- the blow up of
 with center a twisted cubic. The twisted cubic in
with center a twisted cubic. The twisted cubic in  with co-ordinates
with co-ordinates 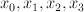 is given by the condition
is given by the condition
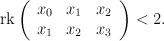
Let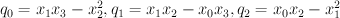 . The relations (szyzgies) between these equations are generated by:
. The relations (szyzgies) between these equations are generated by:
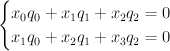
Thus is given by these two equations in
is given by these two equations in 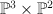 , where the first factor has co-ordinates
, where the first factor has co-ordinates 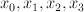 and the second factor has co-ordinates
and the second factor has co-ordinates 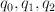 . In other words,
. In other words,  is a complete intersection in
is a complete intersection in 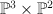 of type
of type 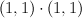 .
.
Quantum Lefschetz gives:
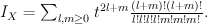
Regularizing this gives period sequence 61:

- the blow-up of
 with centre a plane cubic.
with centre a plane cubic.  is a hypersurface of type
is a hypersurface of type 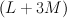 in the toric variety with weight data
in the toric variety with weight data
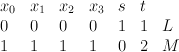 .
.
We have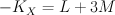 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:
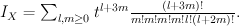
Regularizing this gives period sequence 33:
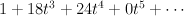
- the blow-up of a quadric 3-fold
 with centre a conic on it.
with centre a conic on it.  is a hypersurface of type
is a hypersurface of type 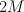 in the toric variety with weight data
in the toric variety with weight data
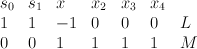 .
.
We have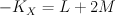 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:
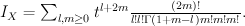
Regularizing this gives period sequence 42:
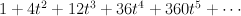
- the blow-up of
 with center a conic.
with center a conic.  is a hypersurface of type
is a hypersurface of type  in the toric variety with weight data
in the toric variety with weight data
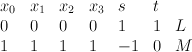 .
.
We have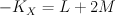 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:
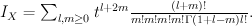
Regularizing this gives period sequence 70:
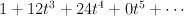
- the blow-up of a quadric 3-fold
 with center a line on it.
with center a line on it.  is a hypersurface of type
is a hypersurface of type 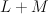 in the toric variety with weight data
in the toric variety with weight data
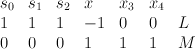 .
.
We have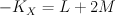 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:
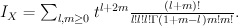
Regularizing this gives period sequence 48:
- a divisor on
 of bidegree
of bidegree 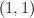 . Quantum Lefschetz gives:
. Quantum Lefschetz gives:
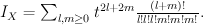
Regularizing this gives period sequence 6:
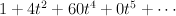
Note that this is a D3 form. - the blow-up of
 with center a line.
with center a line.  is a toric variety with weight data:
is a toric variety with weight data:
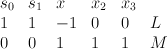 .
.
We have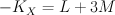 and:
and:

Regularizing this gives period sequence 54:

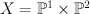 . We have:
. We have:
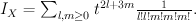
Regularizing this gives period sequence 44:
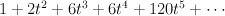
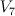 , which is the blow-up of
, which is the blow-up of  at a point. This is a toric variety with weight data:
at a point. This is a toric variety with weight data:
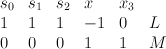 .
.
We have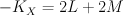 and:
and:
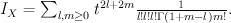
Regularizing this gives period sequence 30:
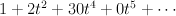
- the scroll
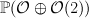 over
over  . This is a toric variety with weight data:
. This is a toric variety with weight data:
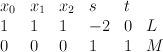 .
.
We have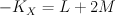 and:
and:
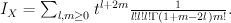
Regularizing this gives period sequence 58:
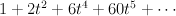
14. This variety X is a section of half-anticanonical class on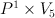 ,
,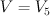 is del Pezzo threefold of degree 5.
is del Pezzo threefold of degree 5.
where
Regularized I-series for V is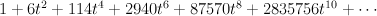
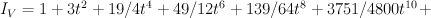
Nonregularized
For line $I_{P^1} = \sum_n \t^{2n} \frac{1}{n!^2}$
For product fourfold we have

So for threefold section X we have to change t^2 to t and do Laplace transform once (for non-regularized):
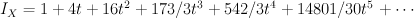
Regularizing gives

After normalization this gives period sequence 39:
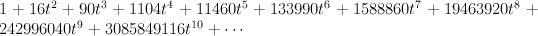
On 17. This is section of half-anticanonical class on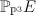 , where $E$ is the null-correlation bundle on
, where $E$ is the null-correlation bundle on 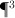 .
.
References are
Wisniewski (1989b)
Ruled Fano 4-folds of index 2
Szurek-Wisniewski (1990b) and $Q^3$.
and $Q^3$.
Fano bundles over
Szurek-Wisniewski (1990c) and $Q_3$.
and $Q_3$.
Fano bundles of rank 2 on