Bumsig Kim explained me how their beautiful theory provides a tool for computing J-series of 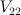 and many other Fano threefolds.
and many other Fano threefolds.
The computation for 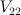 can be reproduced by the following pari/gp code (I omit checking that mirror map is almost trivial):
can be reproduced by the following pari/gp code (I omit checking that mirror map is almost trivial):
N=9
o = O(t^(N+1))
h(n) = sum(k=1,n,1/k)
hh(n) = sum(k=1,n,sum(l=k+1,n,1/k/l))
gg(x, p) = (x!*(1+h(x)*p+hh(x)*p^2+O(u^4)))
simplemirrormap(F) = F * exp(-polcoeff(F,1,t)*t)
reg(F) = sum(n=0,N,t^n*polcoeff(F,n,t)*n!)+O(t^(N+1))
period(F) = reg(simplemirrormap(F))
gp > v22 = period( polcoeff( sum(a=0,N,sum(b=0,N,sum(c=0,N,o+ t^(a+b+c)* ( gg(a+b,u*(A+B)) * gg(a+c,u*(A+C)) * gg(b+c,u*(B+C)) )^3 / (gg(a,u*A) * gg(b,u*B) * gg(c,u*C) )^7 *(c-b+u*(C-B))*(c-a+u*(C-A))*(b-a+u*(B-A)) ))) + O(u^4) , 3,u) /(C-B)/(C-A)/(B-A) + o )
%2 = 1 + 12*t^2 + 60*t^3 + 636*t^4 + 5760*t^5 + 58620*t^6 + 604800*t^7 + 6447420*t^8 + O(t^9)
Indeed, period sequence 17.
Note that 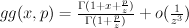 is the familiar Gamma-factor with
is the familiar Gamma-factor with 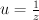 .
.
——————————————————-
So, how does it works?
Consider 3-dimensional vector space 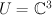 with a fixed base, 7-dimensional vector space
with a fixed base, 7-dimensional vector space 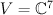 , and space
, and space 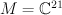 of 3×7 matrices
of 3×7 matrices 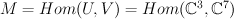
Group 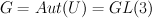 acts on M by left multiplication. It has a subgroup
acts on M by left multiplication. It has a subgroup 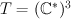 of diagonal matrices and one may restrict the action to this smaller subgroup.
of diagonal matrices and one may restrict the action to this smaller subgroup.
Let 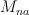 be the subset of matrices of maximal rank and
be the subset of matrices of maximal rank and 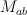 be the subset of matrices with non-vanishing rows,
be the subset of matrices with non-vanishing rows, 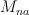 is an open subset in
is an open subset in 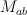 .
.
Consider quotient spaces 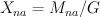 and
and 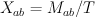 . Note that
. Note that 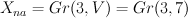 and
and 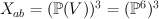 .
.
Since T is a subgroup of G, there is a natural rational map 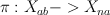 : a triple of points in
: a triple of points in  is sent to their linear span.
is sent to their linear span.
Weyl group (symmetric group 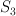 ) acts on
) acts on 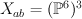 and hence it acts on the cohomology
and hence it acts on the cohomology 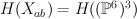 , so cohomology space is decomposed into representations of
, so cohomology space is decomposed into representations of 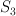 .
.
[I’ll omit the part of the story with the partial flag space and non-holomorphic map].
1. It turns out that cohomology 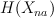 can be identified with antisymmetric part of
can be identified with antisymmetric part of 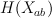 as a graded vector space (with grading shifted by 3).
as a graded vector space (with grading shifted by 3).
Explicitly, 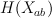 is generated by 3 pullbacks
is generated by 3 pullbacks 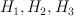 of hyperplane sections on
of hyperplane sections on  ; cohomologies of Grassmanian are known to be quotient of symmetric polynomials. Vector space of anti-symmetric polynomials is obtained from vector space of symmetric polynomials via multiplication by anti-symmetric polynomial of the smallest degree
; cohomologies of Grassmanian are known to be quotient of symmetric polynomials. Vector space of anti-symmetric polynomials is obtained from vector space of symmetric polynomials via multiplication by anti-symmetric polynomial of the smallest degree ![Formula does not parse: \Delta = \prod_{i<j} (s_i-s_j)[/latex]. So cohomology class in Grassmanian corresponding to symmetric function [latex]\sigma[/latex] is sent into [latex]\Delta \cup \sigma(H_1,H_2,H_3)[/latex]. <b>2.</b>Also we can compare vector bundles on [latex]X_{ab} Formula does not parse: \Delta = \prod_{i<j} (s_i-s_j)[/latex]. So cohomology class in Grassmanian corresponding to symmetric function [latex]\sigma[/latex] is sent into [latex]\Delta \cup \sigma(H_1,H_2,H_3)[/latex]. <b>2.</b>Also we can compare vector bundles on [latex]X_{ab}]() and
and 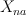 by pulling them back to M, and considering as G-linearized.
by pulling them back to M, and considering as G-linearized.
It turns out that universal bundle U over Gr(3,7) decomposes into sum of 3 line bundles on 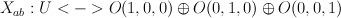 .
.
So 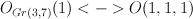 and
and 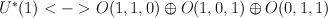 .
.
3. On domain of 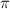 one may define a relative tangent bundle
one may define a relative tangent bundle 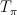 (“traceless” part of
(“traceless” part of 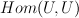 ). It turns out this vector bundle can be extended as a split vector bundle to whole
). It turns out this vector bundle can be extended as a split vector bundle to whole 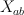 :
: 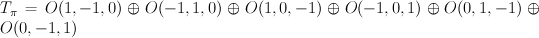 .
.
Consider “square root” of relative tangent bundle 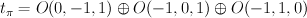 .
.
4.Recall that Fano threefolds 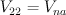 are sections of homogeneous vector bundle
are sections of homogeneous vector bundle 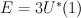 on
on 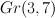 . Comparision (2) shows these threefolds has 9-dimensional abelianizations
. Comparision (2) shows these threefolds has 9-dimensional abelianizations 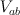 — complete intersections of $9$-dimensional split bundle
— complete intersections of $9$-dimensional split bundle 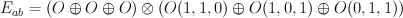 on
on 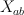 .
.
5. Abelian/non-abelian correspondence is similar for pairs 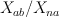 and
and 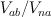 .
.
J-series for Gr(3,7) can be obtained as twisted by relative tangent bundle 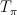 I-series for
I-series for 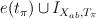 after the comparision of cohomologies described in (1).
after the comparision of cohomologies described in (1).
Similarly, J-series for 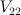 can be obtained via mirror map from twisted by
can be obtained via mirror map from twisted by 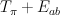 I-series
I-series 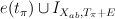 after the “pullbacked” comparision (1).
after the “pullbacked” comparision (1).
6. The sign comes from considering closely the Gamma-factor for relative tangent bundle 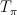 . Note that fibers of abelian/non-abelian correspondence are in some sense holomorphic symplectic (relative tangent bundle contains both O(D) and O(-D)), so they behave like varieties with trivial canonical class.
. Note that fibers of abelian/non-abelian correspondence are in some sense holomorphic symplectic (relative tangent bundle contains both O(D) and O(-D)), so they behave like varieties with trivial canonical class.
Consider the factor 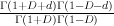 . Since
. Since 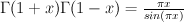 and
and  we have
we have 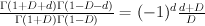 .
.
The same method can also be applied to complete intersections of homogeneous bundles in orthogonal isotropic and symplectic isotropic Grassmanians, since these Grassmanians themselves are just sections of some homogeneous bundles (wedge or symmetric powers of universal bundle) on ordinary Grassmanians of type A. Also this can be uprgaded to treat different blowups of these varieties. In particular, in the comments to this post I compute J-series for Fano threefolds 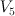 , #2.14, #2.17, #2.20, #2.21 and #2.22.
, #2.14, #2.17, #2.20, #2.21 and #2.22.
Also Bumsig points out that one can express the ab/non-ab twist as a differential operator applied to abelian multi-parameter J-function (basically, just Vandermonde  . This interpretation is more useful for dealing with Frobenius manifolds.
. This interpretation is more useful for dealing with Frobenius manifolds.
References:
Gromov-Witten Invariants for Abelian and Nonabelian Quotients by Aaron Bertram, Ionut Ciocan-Fontanine, Bumsig Kim
The Abelian/Nonabelian Correspondence and Frobenius Manifolds by Ionut Ciocan-Fontanine, Bumsig Kim, Claude Sabbah
Quantum cohomology of the Grassmannian and alternate Thom-Sebastiani by Bumsig Kim, Claude Sabbah
 be a nodal toric Fano threefold (recall that in toric world terminal Gorenstein singularities of Fano threefolds are simply ordinary double points aka nodes
be a nodal toric Fano threefold (recall that in toric world terminal Gorenstein singularities of Fano threefolds are simply ordinary double points aka nodes ![(xy=zt) \subset \CC^4 = \mathrm{Spec } \CC[x,y,z,t] (xy=zt) \subset \CC^4 = \mathrm{Spec } \CC[x,y,z,t]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/232/2322caf126e6be2e67d7eb088fd671e9-ffffff-000000-0.png) ).
). ,
,
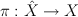
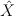 ,
,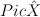 to
to 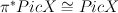 .
.![(a,b) \to \int_{[X]} a \cup b \cup c_1(X) (a,b) \to \int_{[X]} a \cup b \cup c_1(X)](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/bc1/bc107c1ee4b059ffa052e7bdad6cce49-ffffff-000000-0.png)
![\int_{[X]} c_1(X)^3 \int_{[X]} c_1(X)^3](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/ccc/cccf259f6d55f73d0b09adfa44414f00-ffffff-000000-0.png)
 in
in 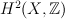 )
)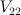 and many other Fano threefolds.
and many other Fano threefolds.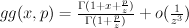 is the familiar Gamma-factor with
is the familiar Gamma-factor with 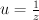 .
.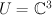 with a fixed base, 7-dimensional vector space
with a fixed base, 7-dimensional vector space 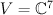 , and space
, and space 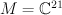 of 3×7 matrices
of 3×7 matrices 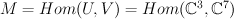
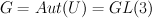 acts on M by left multiplication. It has a subgroup
acts on M by left multiplication. It has a subgroup 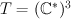 of diagonal matrices and one may restrict the action to this smaller subgroup.
of diagonal matrices and one may restrict the action to this smaller subgroup.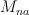 be the subset of matrices of maximal rank and
be the subset of matrices of maximal rank and 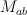 be the subset of matrices with non-vanishing rows,
be the subset of matrices with non-vanishing rows, 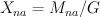 and
and 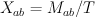 . Note that
. Note that 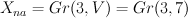 and
and 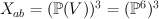 .
.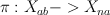 : a triple of points in
: a triple of points in  is sent to their linear span.
is sent to their linear span.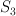 ) acts on
) acts on 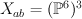 and hence it acts on the cohomology
and hence it acts on the cohomology 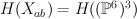 , so cohomology space is decomposed into representations of
, so cohomology space is decomposed into representations of 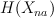 can be identified with antisymmetric part of
can be identified with antisymmetric part of 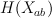 as a graded vector space (with grading shifted by 3).
as a graded vector space (with grading shifted by 3).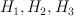 of hyperplane sections on
of hyperplane sections on 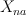 by pulling them back to M, and considering as G-linearized.
by pulling them back to M, and considering as G-linearized.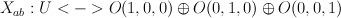 .
.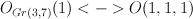 and
and 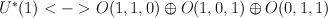 .
.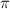 one may define a relative tangent bundle
one may define a relative tangent bundle 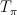 (“traceless” part of
(“traceless” part of 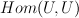 ). It turns out this vector bundle can be extended as a split vector bundle to whole
). It turns out this vector bundle can be extended as a split vector bundle to whole 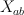 :
: 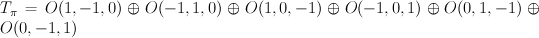 .
.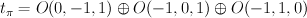 .
.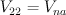 are sections of homogeneous vector bundle
are sections of homogeneous vector bundle 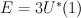 on
on 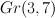 . Comparision (2) shows these threefolds has 9-dimensional abelianizations
. Comparision (2) shows these threefolds has 9-dimensional abelianizations 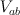 — complete intersections of $9$-dimensional split bundle
— complete intersections of $9$-dimensional split bundle 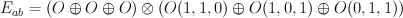 on
on 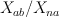 and
and 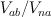 .
.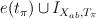 after the comparision of cohomologies described in (1).
after the comparision of cohomologies described in (1).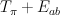 I-series
I-series 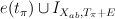 after the “pullbacked” comparision (1).
after the “pullbacked” comparision (1).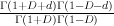 . Since
. Since 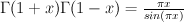 and
and  we have
we have 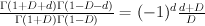 .
. , #2.14, #2.17, #2.20, #2.21 and #2.22.
, #2.14, #2.17, #2.20, #2.21 and #2.22. . This interpretation is more useful for dealing with Frobenius manifolds.
. This interpretation is more useful for dealing with Frobenius manifolds.