Higher rank Fano 3-folds
Rank 4 Fanos
- This is divisor of degree (1,1,1,1) on
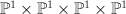
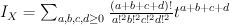
Regularizing gives period sequence 3:
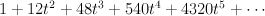
- the blow-up of the cone over a smooth quadric surface
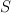 in
in  with center the disjoint union of the vertex and an elliptic curve on
with center the disjoint union of the vertex and an elliptic curve on  . The blow-up of the cone over
. The blow-up of the cone over  with center the vertex is the toric variety with weight data:
with center the vertex is the toric variety with weight data:
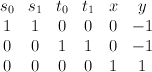
The morphism to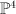 is given by
is given by ![[s_0 : s_1 : t_0 : t_1 : x : y] \mapsto [x : y s_0 t_0 : y s_1 t_1 : y s_0 t_1 : y s_1 t_0] [s_0 : s_1 : t_0 : t_1 : x : y] \mapsto [x : y s_0 t_0 : y s_1 t_1 : y s_0 t_1 : y s_1 t_0]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/34f/34f69bbb4d5548922557cc2abf7f35fc-ffffff-000000-0.png) ; the image here is
; the image here is 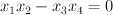 in
in 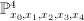 . To obtain
. To obtain  , we blow up the elliptic curve
, we blow up the elliptic curve 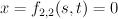 . Thus
. Thus  is the hypersurface
is the hypersurface 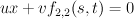 in the toric variety with weight data:
in the toric variety with weight data:
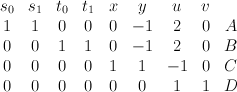
Quantum Lefschetz gives:
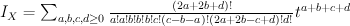
and regularizing gives period sequence 32:
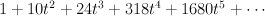
- The blow-up of
 with center a curve
with center a curve  of tridegree (1,1,2). We can take
of tridegree (1,1,2). We can take  to be parametrized as
to be parametrized as ![[s_0:s_1] \mapsto [s_0:s_1:s_0:s_1:s_0^2:s_1^2] \subset \PP^1_{x_0,x_1} \times \PP^1_{y_0,y_1} \times \PP^1_{z_0,z_1} [s_0:s_1] \mapsto [s_0:s_1:s_0:s_1:s_0^2:s_1^2] \subset \PP^1_{x_0,x_1} \times \PP^1_{y_0,y_1} \times \PP^1_{z_0,z_1}](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/dfe/dfe643a09283ccea3081aadf25efff7a-ffffff-000000-0.png) . We embed
. We embed 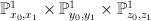 into
into 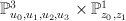 via the map
via the map 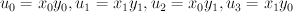 . Now, in
. Now, in 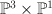 ,
,  becomes the complete intersection defined by equations:
becomes the complete intersection defined by equations:
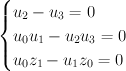
Note that the second equation here is just the equation of inside
inside 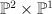 . Thus we can blow up
. Thus we can blow up 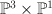 along the locus:
along the locus:
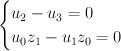
and then construct by imposing the strict transform of the remaining equation
by imposing the strict transform of the remaining equation 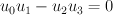 . This exhibits
. This exhibits  as a complete intersection of type
as a complete intersection of type 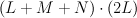 inside the toric variety with weight data:
inside the toric variety with weight data:
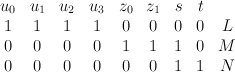
Note that this is rank 4 even though the ambient space has rank 3; there is no contradiction here since the line bundle is not ample and so Lefschetz fails. Quantum Lefschetz (which does not fail) gives:
is not ample and so Lefschetz fails. Quantum Lefschetz (which does not fail) gives:
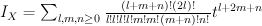
and regularizing gives period sequence 122:
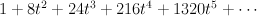 A cleaner and more systematic development is as follows. The curve
A cleaner and more systematic development is as follows. The curve  is defined scheme-theoretically by the equations:
is defined scheme-theoretically by the equations:
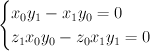
inside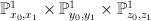 . (Please look at the parametrization given above.) So
. (Please look at the parametrization given above.) So  is given by the equation
is given by the equation 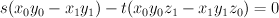 inside the toric variety with weight data:
inside the toric variety with weight data:
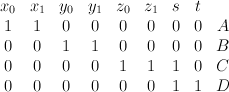
Now Quantum Lefschetz gives:

and regularizing gives period sequence 122:
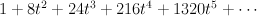
- the blow-up of
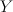 (rank 3, number 19; the blow-up of a quadric with center two non-colinear points
(rank 3, number 19; the blow-up of a quadric with center two non-colinear points 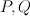 ) with center the strict transform of a conic containing
) with center the strict transform of a conic containing  and
and  . Consider the line
. Consider the line 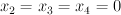 inside
inside 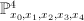 , and also the plane
, and also the plane 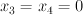 . Let
. Let 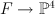 be the blow-up of the line followed by the strict transform of the plane (in that order); this is the toric variety with weight data:
be the blow-up of the line followed by the strict transform of the plane (in that order); this is the toric variety with weight data:
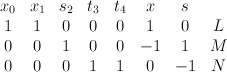
The variety is the strict transform of a general quadric in
is the strict transform of a general quadric in 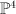 ; in other words it is a hypersurface of type
; in other words it is a hypersurface of type 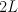 in
in  . (Note that
. (Note that  is rank 4 even though the ambient space is rank 3; there is no contradiction here because
is rank 4 even though the ambient space is rank 3; there is no contradiction here because 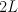 is not ample.) Quantum Lefschetz gives:
is not ample.) Quantum Lefschetz gives:
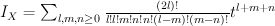
and regularizing gives period sequence 103:
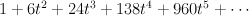
- The blow-up of
 with center two disjoint curves, one of bidegree (2,1) and the other of bidegree (1,0). This is a hypersurface of type
with center two disjoint curves, one of bidegree (2,1) and the other of bidegree (1,0). This is a hypersurface of type 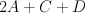 in the toric variety with weight data:
in the toric variety with weight data:
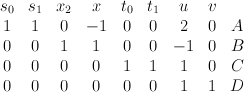
Quantum Lefschetz gives:
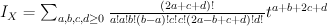
and regularizing gives period sequence 147:
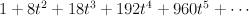
- the blow-up of
 with center the curve of tridegree (1,1,1). This curve is cut out of
with center the curve of tridegree (1,1,1). This curve is cut out of 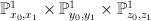 by the equations
by the equations
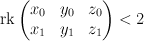
Thus the blow-up is cut out of the toric variety with weight data:
is cut out of the toric variety with weight data:

by the equation:
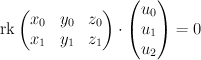
Quantum Lefschetz gives:
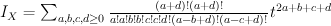
and regularizing gives period sequence 65:
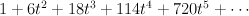
- The blow-up of
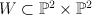 (a divisor of type (1,1)) with center two disjoint curves on it, of bidegree (0,1) and (1,0). We define
(a divisor of type (1,1)) with center two disjoint curves on it, of bidegree (0,1) and (1,0). We define 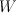 as the zero locus of
as the zero locus of 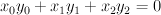 inside
inside 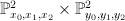 . Blowing up the disjoint union of
. Blowing up the disjoint union of 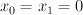 and
and 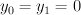 in
in 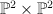 induces the blow-up that we seek. Thus
induces the blow-up that we seek. Thus  is a hypersurface of type
is a hypersurface of type 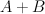 in the toric variety with weight data:
in the toric variety with weight data:
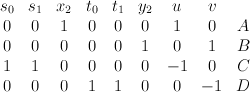
Quantum Lefschetz gives:

and regularizing gives period sequence 69:
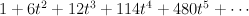
- the blow-up of
 with center a curve
with center a curve  of tridegree (0,1,1). The curve
of tridegree (0,1,1). The curve  is cut out of
is cut out of 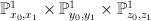 by the equations
by the equations
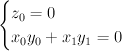
and so is cut out of the toric variety with weight data:
is cut out of the toric variety with weight data:

Quantum Lefschetz gives:
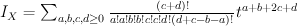
and regularizing gives period sequence 105:
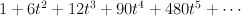
- This is the toric variety with weight data:
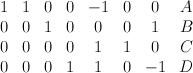
Its regularized period sequence is period sequence 102:
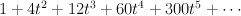
- This is the toric variety with weight data:
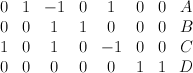
Its regularized period sequence is period sequence 142:

- This is the toric variety with weight data:
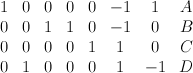
Its regularized period sequence is period sequence 93:
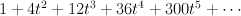
- This is the toric variety with weight data:
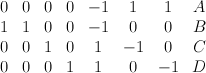
Its regularized period sequence is period sequence 150:
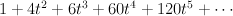
- (degree 26, see the erratum)
This is the blow-up of along a curve
along a curve  of tridegree (1,1,3). Note that
of tridegree (1,1,3). Note that  is a complete intersection of type
is a complete intersection of type 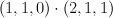 , and thus we can realize
, and thus we can realize  as a hypersurface of type
as a hypersurface of type 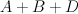 in the toric variety
in the toric variety  with weight data:
with weight data:
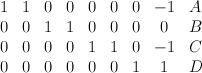
We have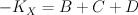 . This is ample on
. This is ample on  but only semi-positive on the ambient space
but only semi-positive on the ambient space  . Thus we are in the situation described here, and we use the same notation. We have:
. Thus we are in the situation described here, and we use the same notation. We have:
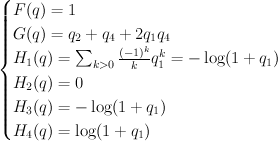
Inverting the mirror map gives:
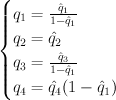
Thus the cohomological-degree-zero part of the J-function of is:
is:
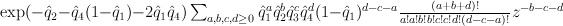
We construct the regularized period sequence from this by making the change of variables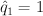 ,
, 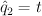 ,
, 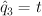 ,
, 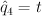 ,
, 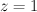 :
:
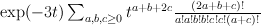
and then doing the trick with factorials:
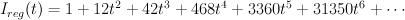
This is period sequence 88.
Rank 5 Fanos
- the blowup of
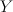 , where
, where 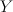 is number 29 on the rank-2 list (i.e. the blow-up of the quadric 3-fold
is number 29 on the rank-2 list (i.e. the blow-up of the quadric 3-fold  with center a conic), with center 3 exceptional lines of the blow-up
with center a conic), with center 3 exceptional lines of the blow-up 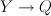 . To compute this, take the defining equation of the quadric to be
. To compute this, take the defining equation of the quadric to be
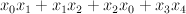
in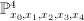 and blow up the ambient space
and blow up the ambient space 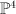 in the plane
in the plane 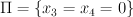 . Note that the conic in $\Pi$ contains the co-ordinate points
. Note that the conic in $\Pi$ contains the co-ordinate points ![[1:0:0], [0:1:0], [0:0:1] [1:0:0], [0:1:0], [0:0:1]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/f94/f94c2ffa696dbd0dd92e2b842b4277f2-ffffff-000000-0.png) . Blowing up the exceptional lines over these points exhibits
. Blowing up the exceptional lines over these points exhibits  as a hypersurface of type
as a hypersurface of type 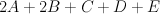 in the toric variety with weight data:
in the toric variety with weight data:

The regularized period sequence is:
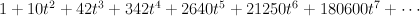
This is period sequence 114. - This is the toric variety with weight data:

The regularized period sequence is:
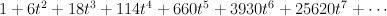
This is period sequence 87. 
The I-function is the product:
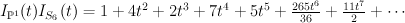
and the regularized period sequence is:
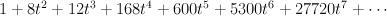
This is period sequence 43.
Rank > 5 Fanos
These are products 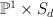 of line with del Pezzo surface of degree
of line with del Pezzo surface of degree 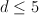 . The I-series are products of I-series for line and for del Pezzo surfaces.
. The I-series are products of I-series for line and for del Pezzo surfaces.
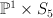 . We have:
. We have:

The regularized period is:
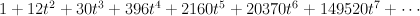
This is period sequence 64.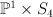 . We have:
. We have:
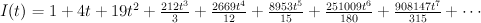
The regularized period is:
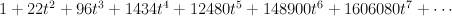
This is period sequence 71.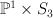 . We have:
. We have:
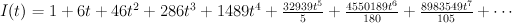
The regularized period is:
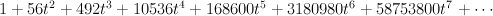
This is period sequence 45.- [Not very Fano]
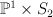 . We have:
. We have:
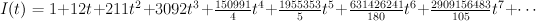
The regularized period is:
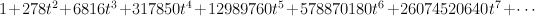
This period sequence is non-Gorenstein. - [Not very Fano]
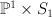 . We have:
. We have:

The regularized period is:
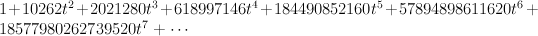
This period sequence is non-Gorenstein.
How to make history of this and two other pages trackable?
I’m not sure. You can use the RSS feeds for posts and comments, but I don’t know how to check easily (i.e. via RSS or similar) that a page has been edited. Do you use Twitter? If you like I can set things up so that you get a tweet every time I make a significant change to a page.
Ok, I just registered there with username ‘serugey’