September 22, 2010, 12:09 pm
Here are my (incomplete) notes from Batyrev’s talk in the Extremal Laurent Polynomials workshop at Imperial:
Batyrev_London_Sep_2010
If you have complete notes, please post them here.
Partial summary:
- spherical varieties
- a model family of examples:
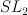 -varieties
-varieties
- review: compactification and toric varieties
- spherical compactification in these examples
- valuations and coloured cones
- finding toric degenerations
September 22, 2010, 12:04 pm
Here are my notes from Altmann’s talk at the Extremal Laurent Polynomials workshop at Imperial:
Altmann_London_Sep_2010
Summary:
- an example due to Pinkham
- deformations and Minkoski sums; a lattice condition
- constructing the deformation corresponding to a Minkwoski decomposition
- the versal deformation space and the moduli space of generalized Minkowski summands of Q
- Example: the cone over a hexagon
- the equations defining the versal deformation space in the isolated Gorenstein case
- a new point of view: double divisors
September 22, 2010, 11:58 am
Here are my notes from Siebert’s talk at the Extremal Laurent Polynomials workshop at Imperial:
Siebert_London_Sep_2010
Summary:
- An overview of toric degenerations and the Gross–Siebert picture
- Examples: a pencil of quartics in
 and a pencil of elliptic curves in
and a pencil of elliptic curves in 
- the Gross–Siebert Reconstruction Theorem
- Mirror Symmetry and the discrete Legendre Transform
- Landau–Ginzburg models; the Hori–Vafa mirror
- how to extend the superpotential from the central fiber to the whole of the mirror family in such a way that the resulting superpotential is proper
- Example:
 , flattening the boundary of the polyhedral complex
, flattening the boundary of the polyhedral complex
- Broken lines and scattering
September 22, 2010, 11:50 am
Here are my notes from Golshev’s talk at the Extremal Laurent Polynomials workshop at Imperial:
Golyshev_London_Sep_2010
Summary:
- a historical analogy: the study of Fano varieties now versus the study of algebraic varieties in the early 1970s
- the key idea: classifying Fanos by detecting and classifying Fano quantum motives and their realizations
- possible approaches
- the Tannakian picture
- the quantum Satake correspondence (Golyshev–Manivel)
- two steps in this direction: Ueda’s proof of the Dubrovin Conjecture for
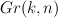 ; Galkin–Golyshev–Iritani’s proof that Apery=Gamma
; Galkin–Golyshev–Iritani’s proof that Apery=Gamma
- irregular monodromy data for Dubrovin’s quantum connection
- the Extended Dubrovin Conjecture and the Apery=Gamma hypothesis
- the Extended Dubrovin Conjecture and the Apery=Gamma hypothesis hold for
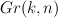
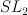 -varieties
-varieties and a pencil of elliptic curves in
and a pencil of elliptic curves in 
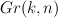 ; Galkin–Golyshev–Iritani’s proof that Apery=Gamma
; Galkin–Golyshev–Iritani’s proof that Apery=Gamma