Let X be a smooth Fano threefold with Picard number P = 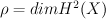 .
.
Then subring of algebraic (even) cycles in X is (2+2P)-dimensional, and its Lefschetz decomposition has P blocks: 1 block of length 4 and (P-1) blocks of length 2. So its image in cohomologies of anticanonical section (K3 surface) is (2+2P – P) = (2+P)-dimensional.
For “general” Fano threefold with Picard number P we expect
regularized quantum differential equation (RQDE) to be of degree (2+P) in 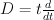
and to have (2+2P) singular points. Nevertheless degree in t may be more than number of singular points
due to apparent singularities.
It turns out that condition for general is not very general in practice.
Assume Fano threefold X has action of finite group G in one of the 4 ways:
a. G acts on X by regular (algebraic) transformations,
b. G acts on X by symplectic transformations,
c. X is defined over non-algebraically closed field k and G is Galois group Gal(k),
d. X is a fiber of a smooth family over some base B and fundamental group 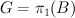 acts on
acts on 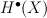 via monodromy.
via monodromy.
For cases a,b,c consider the induced action of G on cohomology of X.
Let p = 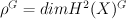 be $G$-invariant Picard number.
be $G$-invariant Picard number.
G-invariant part of cohomologies 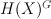 is (2+2p)-dimensional.
is (2+2p)-dimensional.
Define 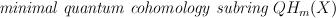 of
of 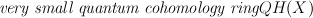 as subring generated by
as subring generated by 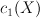 and C[t].
and C[t].
It is easy to see 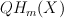 is contained in
is contained in ![H(X, C)^G [t] H(X, C)^G [t]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/f66/f66c236b83bd71fc79b4f33e0ef3c4a4-ffffff-000000-0.png) .
.
This implies that regularized I-series 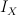 is annihilated by
is annihilated by
differential operator of degree (2+p).
So it is natural to ask about possible G-actions on Fano threefolds.
First (numerical) step is to see the possible automorphisms of Mori cone or Kaehler cone.
We have some structures on 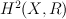 :
:
a. lattice 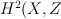 ) and element
) and element 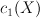 inside the lattice,
inside the lattice,
b. rational polyhedral cone of numerically effective divisors,
c. nondegenerate integral quadratic form (Lefschetz pairing) : 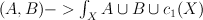 .
.
We call this information  .
.
Group of automorphisms of Mori structure is finite, and for any action
G-invariant Picard number is not less than dimension of invariants of 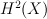
with respect to whole group of automorphisms of Mori structure.
As far as I remember (but cannot find a reference) for all Fano threefolds one may find some moduli
and some kind of G-action such that G-invariant Picard group coincides with invariant part of $H^2$ with respect to automorphisms of Mori structure.
The standard reference for automorphisms of Mori structure is probably:
Kenji Matsuki, “Weyl groups and birational transformations among minimal models”, AMS 1995
He studies slightly different problem, but has a similar answer. Unfortunately I haven’t a copy of this book, but copied one page from google books.
He says automorphisms of Mori structures turn out to be Weyl groups.
He claims the following Fano threefolds have nontrivial automorphisms:
P – Picard number, then list of Mori-Mukai numbers with the given Picard number
P=2:
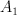 : 2, 6, 12, 21, 32 (these should be G-Fano, but number 2 is suspicious)
: 2, 6, 12, 21, 32 (these should be G-Fano, but number 2 is suspicious)
other have p=2
P=3:
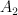 : 1, 27 (G-Fano, suspicious that 13 is in the next line)
: 1, 27 (G-Fano, suspicious that 13 is in the next line)
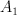 : 3, 7, 9, 10, 13, 17, 19, 20, 25, 31 (should correspond to p=2)
: 3, 7, 9, 10, 13, 17, 19, 20, 25, 31 (should correspond to p=2)
other have p=3
P=4:
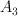 : 1 (G-Fano)
: 1 (G-Fano)
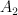 : 6 (p=2)
: 6 (p=2)
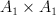 : 2 (p=2)
: 2 (p=2)
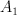 : 3, 4, 7, 8, 10, 12 (p=3)
: 3, 4, 7, 8, 10, 12 (p=3)
trivial – 5,9,11 (should have p=4)
missing number 13 from Erratum
P=5:
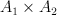 : 3 (p=2)
: 3 (p=2)
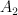 : 1 (p=3)
: 1 (p=3)
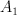 : 2 (p=4)
: 2 (p=4)
For cases 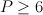 our threefolds are products of a line and del Pezzo surface
our threefolds are products of a line and del Pezzo surface 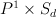 . They all have Weyl group of type
. They all have Weyl group of type 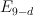 and p=2.
and p=2.
So the distribution in p is the following (case 4.13 is missing):
p is always less than 5;
p=4 – 4 varieties: 5.2; 4.5, 4.9, 4.11
p=3 – 26 varieties: 5.1; 4.3, 4.4, 4.7, 4.8, 4.10, 4.12; and 19 with P=3
p=2 – 50 varieties
p=1 – 25 varieties (or 26 if 2.2 is there)
This means just 4 varieties should have N=6, and other have even less.
The obvious thing to do is to recompute ourselves the Mori structure and its automorphisms
(in particular discriminant of Lefschetz quadratic form is an important invariant that we need anyway).
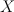 be a nodal toric Fano threefold (recall that in toric world terminal Gorenstein singularities of Fano threefolds are simply ordinary double points aka nodes
be a nodal toric Fano threefold (recall that in toric world terminal Gorenstein singularities of Fano threefolds are simply ordinary double points aka nodes ![(xy=zt) \subset \CC^4 = \mathrm{Spec } \CC[x,y,z,t] (xy=zt) \subset \CC^4 = \mathrm{Spec } \CC[x,y,z,t]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/232/2322caf126e6be2e67d7eb088fd671e9-ffffff-000000-0.png) ).
). ,
,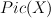
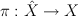
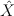 ,
,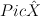 to
to 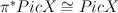 .
.![(a,b) \to \int_{[X]} a \cup b \cup c_1(X) (a,b) \to \int_{[X]} a \cup b \cup c_1(X)](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/bc1/bc107c1ee4b059ffa052e7bdad6cce49-ffffff-000000-0.png)
![\int_{[X]} c_1(X)^3 \int_{[X]} c_1(X)^3](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/ccc/cccf259f6d55f73d0b09adfa44414f00-ffffff-000000-0.png)
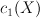 in
in 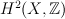 )
)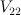 and many other Fano threefolds.
and many other Fano threefolds.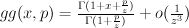 is the familiar Gamma-factor with
is the familiar Gamma-factor with 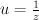 .
.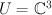 with a fixed base, 7-dimensional vector space
with a fixed base, 7-dimensional vector space 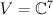 , and space
, and space 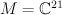 of 3×7 matrices
of 3×7 matrices 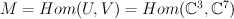
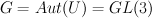 acts on M by left multiplication. It has a subgroup
acts on M by left multiplication. It has a subgroup 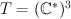 of diagonal matrices and one may restrict the action to this smaller subgroup.
of diagonal matrices and one may restrict the action to this smaller subgroup.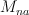 be the subset of matrices of maximal rank and
be the subset of matrices of maximal rank and 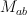 be the subset of matrices with non-vanishing rows,
be the subset of matrices with non-vanishing rows, 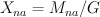 and
and 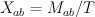 . Note that
. Note that 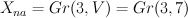 and
and 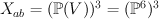 .
.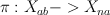 : a triple of points in
: a triple of points in 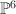 is sent to their linear span.
is sent to their linear span.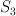 ) acts on
) acts on 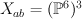 and hence it acts on the cohomology
and hence it acts on the cohomology 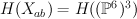 , so cohomology space is decomposed into representations of
, so cohomology space is decomposed into representations of 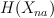 can be identified with antisymmetric part of
can be identified with antisymmetric part of 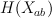 as a graded vector space (with grading shifted by 3).
as a graded vector space (with grading shifted by 3).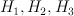 of hyperplane sections on
of hyperplane sections on 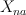 by pulling them back to M, and considering as G-linearized.
by pulling them back to M, and considering as G-linearized.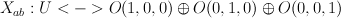 .
.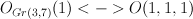 and
and 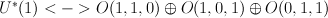 .
. one may define a relative tangent bundle
one may define a relative tangent bundle  (“traceless” part of
(“traceless” part of 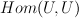 ). It turns out this vector bundle can be extended as a split vector bundle to whole
). It turns out this vector bundle can be extended as a split vector bundle to whole 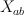 :
: 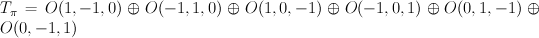 .
.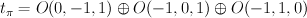 .
.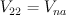 are sections of homogeneous vector bundle
are sections of homogeneous vector bundle 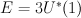 on
on 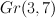 . Comparision (2) shows these threefolds has 9-dimensional abelianizations
. Comparision (2) shows these threefolds has 9-dimensional abelianizations 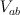 — complete intersections of $9$-dimensional split bundle
— complete intersections of $9$-dimensional split bundle 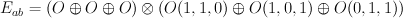 on
on 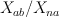 and
and 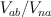 .
.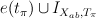 after the comparision of cohomologies described in (1).
after the comparision of cohomologies described in (1).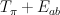 I-series
I-series 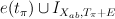 after the “pullbacked” comparision (1).
after the “pullbacked” comparision (1).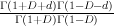 . Since
. Since 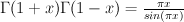 and
and 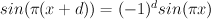 we have
we have 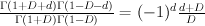 .
.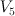 , #2.14, #2.17, #2.20, #2.21 and #2.22.
, #2.14, #2.17, #2.20, #2.21 and #2.22. . This interpretation is more useful for dealing with Frobenius manifolds.
. This interpretation is more useful for dealing with Frobenius manifolds.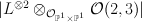 on the
on the 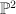 -bundle
-bundle 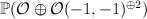 over
over 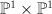 such that
such that 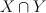 is irreducible, where
is irreducible, where 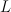 is the tautological line bundle and
is the tautological line bundle and 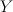 is a member of
is a member of 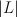 .
. 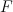 is the toric variety with weight data:
is the toric variety with weight data: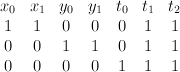
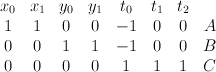
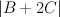 .
.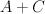 (which restricts to
(which restricts to 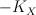 on
on 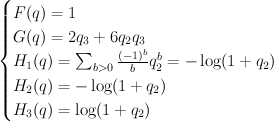
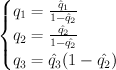
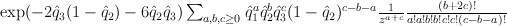
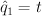 ,
, 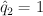 ,
, 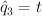 ,
, 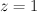 yields:
yields: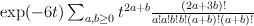
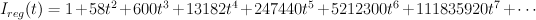
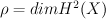 .
.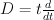
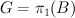 acts on
acts on 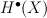 via monodromy.
via monodromy. 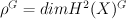 be $G$-invariant Picard number.
be $G$-invariant Picard number.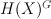 is (2+2p)-dimensional.
is (2+2p)-dimensional.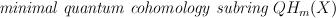 of
of 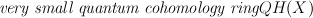 as subring generated by
as subring generated by 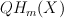 is contained in
is contained in ![H(X, C)^G [t] H(X, C)^G [t]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/f66/f66c236b83bd71fc79b4f33e0ef3c4a4-ffffff-000000-0.png) .
.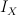 is annihilated by
is annihilated by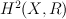 :
: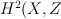 ) and element
) and element 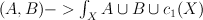 .
.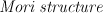 .
.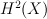
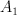 : 2, 6, 12, 21, 32 (these should be G-Fano, but number 2 is suspicious)
: 2, 6, 12, 21, 32 (these should be G-Fano, but number 2 is suspicious)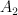 : 1, 27 (G-Fano, suspicious that 13 is in the next line)
: 1, 27 (G-Fano, suspicious that 13 is in the next line)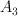 : 1 (G-Fano)
: 1 (G-Fano)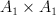 : 2 (p=2)
: 2 (p=2)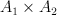 : 3 (p=2)
: 3 (p=2)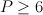 our threefolds are products of a line and del Pezzo surface
our threefolds are products of a line and del Pezzo surface 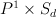 . They all have Weyl group of type
. They all have Weyl group of type  and p=2.
and p=2.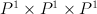
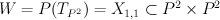 (hyperplane section of product of two planes in Segre embedding).
(hyperplane section of product of two planes in Segre embedding).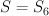 (del Pezzo surface of degree 6).
(del Pezzo surface of degree 6).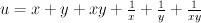
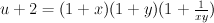
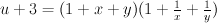
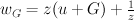
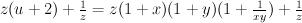
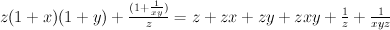
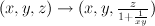 .
.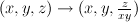 :
: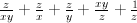
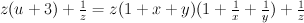
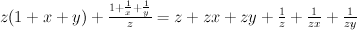
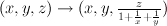
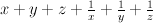
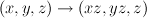 .
. be a 3-dimensional reflexive polytope. We will construct a Laurent polynomial with Newton polytope equal to
be a 3-dimensional reflexive polytope. We will construct a Laurent polynomial with Newton polytope equal to 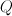 is the lattice Minkowski sum of polygons
is the lattice Minkowski sum of polygons 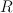 and
and 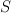 if and only if both:
if and only if both: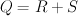 , so that
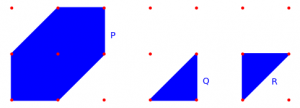
, so that  here are allowed to be degenerate.
here are allowed to be degenerate. of a hexagon:
of a hexagon: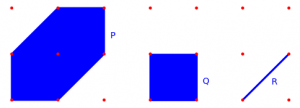
 :
:
 .
.
 of Laurent polynomials; this list will be empty if
of Laurent polynomials; this list will be empty if  elements in the list for facet
elements in the list for facet 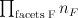 ).
). as a piece of the quantum cohomology local system associated to a smoothing of the Newton polytope of
as a piece of the quantum cohomology local system associated to a smoothing of the Newton polytope of