Unsections/Cones and “Tom vs Jerry” ambiguity
Unsections/Cones and “Tom vs Jerry” ambiguity:
why no single-valued ansatz is possible and Minkowski ambiguity is the thing to expect
[Miles Reid-like notation]
Consider two del Pezzo threefolds of degree 6.
Let Jerry be 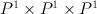
and Tom be 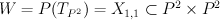 (hyperplane section of product of two planes in Segre embedding).
(hyperplane section of product of two planes in Segre embedding).
It is known that Tom and Jerry are not fibers of a flat family.
Tom has period sequence 6,
Jerry is grdb[520140 and has period sequence 21.
Their half-anticanonical section is 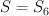 (del Pezzo surface of degree 6).
(del Pezzo surface of degree 6).
So both Tom and Jerry can be degenerated to the same Gorenstein toric Fano threefold — anticanonical cone over S.
This cone has just one integral point except origin and vertices.
Let 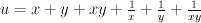
be the normalized Laurent polynomial for the honeycomb (fan polytope of S).
Note that honeycomb has two different Minkowski decompositions — as sum of three intervals and as sum of two triangles.
These decompositions correspond to two different decompositions of (u+G) into the product of Laurent polynomials [for two different values of G (G=2 and G+3)]:
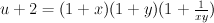
and
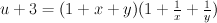
General Laurent polynomial for the cone over S
has the form
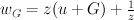
The most interesting thing is the following:
if we choose $G=2$ then w is mirror of Jerry,
but if we choose $G=3$ then w is mirror of Tom.
Moreover applying mutation we can transform w to terminal Gorenstein polynomials:
————
[tom]
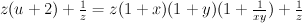
becomes 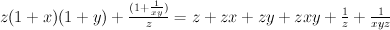
by applying 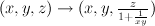 .
.
This corresponds to STD of Tom.
It looks nicer after monomial transformation 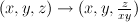 :
:
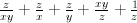
————
[jerry]
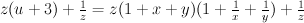
becomes 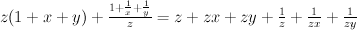
by applying 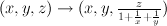
This is simply Laurent polynomial for the smooth model of Jerry:
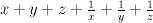
after monomial transformation
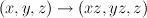 .
.
————-
So Laurent phenomenon distinguishes degenerations of different varieties to the same singular and does not mix them.
Tom, Jerry and Spike.
If in the previous scenario we look for bigger brothers of Tom and Jerry with index 1,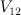 .
.
then we have a pleasant surprise – not only we get 3.1 and 2.6, but also
For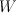 and
and  we constructed mirrors
we constructed mirrors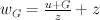 where
where 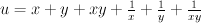 ,
,
as
and G is either 2 or 3.
Regularized I-series for 2.6 and 3.1 has the same coefficients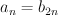 ,
,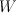 and
and  .
.
so their mirrors should be related to squares of mirrors for
Consider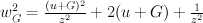 .
.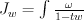 as its isogeneous
as its isogeneous
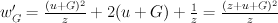
Obviously it has the same
Newton polytope for this kind of Laurent polynomials have number 432464 in grdb.
We can check that
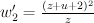 has period sequence 11 and is mirror to 2.6,
has period sequence 11 and is mirror to 2.6,
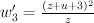 has period sequence 22 and is mirror to 3.1.
has period sequence 22 and is mirror to 3.1.
But we can have even more – I find it very amusing that
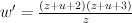 has period sequence 7 and is mirror to
has period sequence 7 and is mirror to 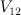 .
.
Since singular toric variety in question is again a cone over surface, probably it won’t be hard to prove the existence of degenerations.