Should start groping for 5-dim’l cousin of V_22
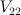 can be characterized as the smooth Fano of index 1 with minimal cohomology. One way to construct its D3 is by assigning 1’s to the vertices of a terminal self-dual polytope.
can be characterized as the smooth Fano of index 1 with minimal cohomology. One way to construct its D3 is by assigning 1’s to the vertices of a terminal self-dual polytope.
Are there terminal self-dual polytopes in dim 5 that produce D5’s whose matrix entries are positive integers?
Am I right in believing that one can search for self-duals considerably more easily than for arbitrary reflexives?
A. If we look for terminal self-dual polytope then in dimensions up to 3 it is unique
d=1. interval –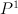 ,
,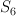 (smooth del Pezzo of degree 6)
(smooth del Pezzo of degree 6)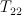 – STD of
– STD of 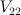
d=2. honeycomb –
d=3.
In dimension 4 there is a unique terminal self-dual 24-cell,
and Benjamin Nill told me once some uniqueness result,
but I forgot the correct formulation – it could be there is nothing except the unique 24-cell.
In dimension 8 there is a polytope corresponding to E_8 root system (convex hull of roots).
B.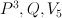 are not self-dual as lattice polytopes, however their duals are their homotheties.
are not self-dual as lattice polytopes, however their duals are their homotheties.
Property “terminal self-dual” can be weakened in two directions to produce two other interesting properties:
I. When dual of terminal polytope is terminal.
II. When Gorenstein polytope is combinatorially self-dual.
II+. When polytope and its dual are homothety-equivalent.
I wonder if there might be a Monte Carlo method to arrive at self-duals by iteration. Start with something random, generate a dual, adjust it to become a lattice polytope, generate a dual, continue.
Then you just end up with reflexive polytope.
Or you need to adjust somehow to terminal.
And then you end with pair of dual reflexive terminals (problem of type I above).