Slicing the data
Sergei: I sliced the Minkowski period data as you requested, here.
Update: here is a new version which also contains the Picard ranks.
A collaborative research blog.
Sergei: I sliced the Minkowski period data as you requested, here.
Update: here is a new version which also contains the Picard ranks.
Sergei: for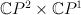 I get
I get 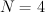 ,
, 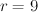 . See period sequence 44.
. See period sequence 44.
OK, not tomorrow. Maybe the next day…
Tom: thank you very much, I figured out my disambiguation.
The problem is the apparent singularities.
Choose a coordinate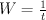 .
.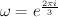 — a root of
— a root of 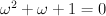 .
.
Choose
For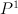 there are two singularities:
there are two singularities: 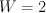 and
and 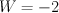 .
.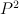 there are three singularities:
there are three singularities: 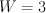 ,
, 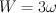 and
and 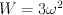 .
.
For
In case of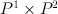 we should have 6 singularities, in coordinate W these are the sums singularities for
we should have 6 singularities, in coordinate W these are the sums singularities for 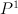 and for
and for 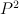 :
: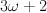 and
and 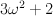 , two roots of a^2 – a + 7 are
, two roots of a^2 – a + 7 are 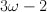 and
and 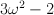 .
.
1=3-2, 5 = 3+2, two roots of a^2+7 a+19 are
In inverse to W coordinate t this should correspond to a product
 in front of D^4.
in front of D^4.
However the symbol of PF equation is not exactly this degree 6 polynomial, but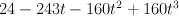 , solutions of this degree 3 equation are apparent singularities – the monodromies around these points are identities.
, solutions of this degree 3 equation are apparent singularities – the monodromies around these points are identities.
degree 9 polynomial in t:
107730*t^9 – 211376*t^8 – 50139*t^7 + 156996*t^6 – 20520*t^5 + 16194*t^4 + 1782*t^3 – 448*t^2 – 243*t + 24
There is an extra factor of
So far I cannot think on an easy cure for these (not involving computing the monodromies).
However it could be useful to check for the decomposition (over integers) of the PF’s symbol – if the symbol is indecomposable and of high degree (more than 10 in general) then it is certainly suspicious.
For smooth Fano threefold with (G-invariant) Picard number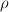 we expect N to be
we expect N to be 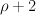 and r to be
and r to be 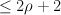 .
.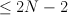 .
.
So we expect the symbol to have some factors of degree
For Picard ranks, could you please add both maximal and minimal ranks that appear?
When Fano has a degeneration to (Gorenstein/any) toric variety with Pic=Z ?
I’ve added a new version containing the Picard ranks.
Sergei: I grabbed these directly from grdb because I couldn’t get your gp code to work. Did you mean concat rather than matconcat?
Sorry about the delay — I was on holiday.
Tom: sorry, indeed I have alias matconcat=concat for backward compatibility.
Here are my .gpalias and .gprc files.
Generally degree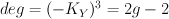 and Picard rank
and Picard rank 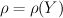 is not enough to determine the smooth Fano Y.
is not enough to determine the smooth Fano Y.
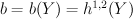 and
and
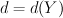 — discriminant of quadratic form
— discriminant of quadratic form  on the lattice Pic(Y).
on the lattice Pic(Y).
We need two more invariants:
For STD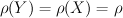 and number b is given by the formula
and number b is given by the formula
where v and f are numbers of vertices and faces of fan polytope.
So number b should also be easily derived from grdb data.
Also for STD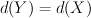 .
.
However I don’t think there is any way to compute this number essentially simpler than the obvious one used in my script.
In case of degeneration to non-terminal Gorenstein variety X Picard number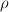 may fall down.
may fall down.
If for some reason Picard number remains the same, then Pic(X) is a sublattice of Pic(Y) of some finite index r. Then
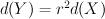 ,
,
but since d(Y) is rarely divisible by a square this happens not so often.
Tom, could you please post a new version which contains both Picard ranks and degrees?
Freshly fixed, updated and improved script for computing the principal invariants of the smoothing