A new ansatz for extremal Laurent polynomials
This post describes a new method for generating Laurent polynomials in 3 variables. Many of these Laurent polynomials are extremal or of low ramification, and they include the extremal Laurent polynomials mirror to 15 of the 17 minimal Fano 3-folds. We call this method the Minkowksi ansatz.
Let  be a 3-dimensional reflexive polytope. We will construct a Laurent polynomial with Newton polytope equal to
be a 3-dimensional reflexive polytope. We will construct a Laurent polynomial with Newton polytope equal to  , or in other words we will explain how to assign a coefficient to each integer point in
, or in other words we will explain how to assign a coefficient to each integer point in  . This goes as follows.
. This goes as follows.
Lattice Minkowski sums
We say that a polygon  is the lattice Minkowski sum of polygons
is the lattice Minkowski sum of polygons 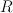 and
and 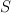 if and only if both:
if and only if both:
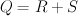 , so that
, so that  is the Minkowski sum of
is the Minkowski sum of 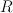 and
and 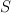 as usual
as usual- the integer lattice in
 is the sum of the integer lattices in
is the sum of the integer lattices in 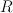 and
and 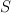 .
.
Note that any of the the polygons  here are allowed to be degenerate.
here are allowed to be degenerate.
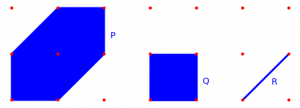
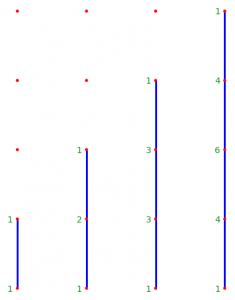
Examples: here are two lattice Minkowksi decompositions 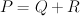 of a hexagon:
of a hexagon:
Note that the same lattice polygon can have more than one lattice Minkowski decomposition. Note also that the first decomposition here is not a complete decomposition into lattice-Minkowksi-irreducible pieces, because the square  can be further decomposed as the sum of a vertical and a horizontal line.
can be further decomposed as the sum of a vertical and a horizontal line.
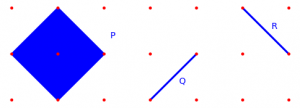
The example above is not a lattice Minkowski decomposition, because the lattice in  is not the sum of the lattices in
is not the sum of the lattices in  and
and 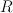 . In fact
. In fact  is lattice Minkowski irreducible.
is lattice Minkowski irreducible.
Decompose the facets into irreducible pieces
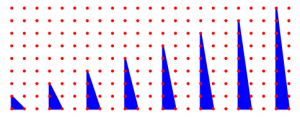
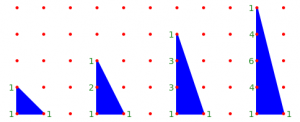
There are 4319 3-dimensional reflexive polytopes. These polytopes contain a total of 344 distinct facets, where we regard two facets as the same if and only if they differ by a lattice-preserving automorphism. Of these facets, 79 are lattice Minkowski irreducible. These 79 facets are also the non-degenerate polygons which occur when the 344 total facets are decomposed into lattice Minkowksi irreducible pieces. Of those 79 facets, exactly 8 contain no interior lattice points. Those 8 triangles, which we call admissible triangles are all of type 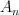 :
:
In other words, the cones over these triangles give affine toric varieties that are transverse 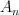 singularities, for
singularities, for 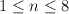 .
.
The ansatz
Given a 3-dimensional reflexive polytope  , we construct a possibly-empty list of Laurent polynomials as follows. For each facet
, we construct a possibly-empty list of Laurent polynomials as follows. For each facet  of
of  , decompose
, decompose  into lattice-Minkowksi-irreducible pieces in all possible ways. Discard any such decomposition of
into lattice-Minkowksi-irreducible pieces in all possible ways. Discard any such decomposition of  which contains a non-degenerate polygon that is not an admissible triangle. Any remaining decomposition of
which contains a non-degenerate polygon that is not an admissible triangle. Any remaining decomposition of  will consist of line segments and admissible triangles. To this decomposition we associate a Laurent polynomial which is the product of certain basic Laurent polynomials corresponding to line segments and to admissible triangles. The basic Laurent polynomials for admissible triangles are:
will consist of line segments and admissible triangles. To this decomposition we associate a Laurent polynomial which is the product of certain basic Laurent polynomials corresponding to line segments and to admissible triangles. The basic Laurent polynomials for admissible triangles are:
and so on for the remaining admissible triangles. The basic Laurent polynomials for line segments are:
and so on for other line segments.
So now, for each facet  of
of  , we have a list
, we have a list  of Laurent polynomials; this list will be empty if
of Laurent polynomials; this list will be empty if  cannot be written as a lattice Minkowksi sum of line segments and admissible triangles. In other words for each facet
cannot be written as a lattice Minkowksi sum of line segments and admissible triangles. In other words for each facet  we have list of ways of assigning coefficients to each integer point in
we have list of ways of assigning coefficients to each integer point in  . We seek a list of Laurent polynomials with Newton polytope equal to
. We seek a list of Laurent polynomials with Newton polytope equal to  , or in other words a list of ways of assigning coefficients to each integer point in
, or in other words a list of ways of assigning coefficients to each integer point in  . This is produced by assigning the coefficient zero to the origin (which is the only interior point of
. This is produced by assigning the coefficient zero to the origin (which is the only interior point of  ) and then assigning coefficients to the integer points on facets of
) and then assigning coefficients to the integer points on facets of  as specified in the facet lists (but amalgamated in all possible ways, so if there are
as specified in the facet lists (but amalgamated in all possible ways, so if there are 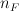 elements in the list for facet
elements in the list for facet  then the number of elements in the list for
then the number of elements in the list for  is
is 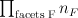 ).
).
Points to Note
- This ansatz almost generalizes the earlier recipes given by Pryjzalkowski and Galkin, but differs a little because of the difference between Minkowski decomposition and lattice Minkowksi decomposition.
- Altman has studied the deformation theory of affine toric varieties and discovered a close connection with Minkowski decompositions. Since we expect to find the local system associated to an extremal Laurent polynomial
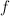 as a piece of the quantum cohomology local system associated to a smoothing of the Newton polytope of
as a piece of the quantum cohomology local system associated to a smoothing of the Newton polytope of 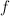 , this is encouraging. But note that Minkowski decomposition and lattice Minkowksi decomposition are not the same.
, this is encouraging. But note that Minkowski decomposition and lattice Minkowksi decomposition are not the same. - We suspect that if
 is a 3-dimensional reflexive polytope containing a facet with no admissible lattice Minkowski decompositions then the toric variety corresponding to
is a 3-dimensional reflexive polytope containing a facet with no admissible lattice Minkowski decompositions then the toric variety corresponding to  does not smooth. More on this later.
does not smooth. More on this later. - This ansatz also fits well with Kouchnirenko’s criterion for a Laurent polynomial to be degenerate.
(I learned this last point from Hiroshi.)

You mean the singularity corresponding to the cone over this facet does not admit a smoothing?
The ansatz looks reasonable, since it obviously respects the simplest type of the symplectomorphisms
where
and
the product corresponds to some Minkowski decomposition of the facet supporting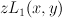 i.e.
i.e. 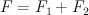 and
and 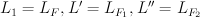 .
.
I expect there is an ansatz like that for all smoothable polytopes (maybe not Gorenstein).
Note that my original post contained a mistake which I have now corrected: the only change is the description of how to go from a collection of lists of Laurent polynomials, one for each facet, to a list of Laurent polynomials for the polytope .
.
Sergei: does your comment 2 still apply to this corrected version?
@Sergei: with regard to comment 1, what Alessio expects is that if a 3d reflexive polytope contains a face
contains a face  without admissible decompositions then the toric variety
without admissible decompositions then the toric variety 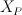 corresponding to
corresponding to  is not smoothable. This is precisely because, as you suggest, he expects that the toric co-ordinate patch on
is not smoothable. This is precisely because, as you suggest, he expects that the toric co-ordinate patch on 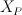 corresponding to the cone over
corresponding to the cone over  will not smooth. But even if each face of
will not smooth. But even if each face of  is such that the cone over it gives a smoothable affine toric variety, I expect that there may still be some global obstruction to smoothability because the local smoothings (i.e. the smoothings of the toric co-ordinate patches) may not glue together to give a smoothing of the whole toric variety.
is such that the cone over it gives a smoothable affine toric variety, I expect that there may still be some global obstruction to smoothability because the local smoothings (i.e. the smoothings of the toric co-ordinate patches) may not glue together to give a smoothing of the whole toric variety.
I cannot see what was the typo, but my comment2 is a positive feedback to the ansatz you wrote now — if there are two parallel facets, you can transmit some of their divisors between them.
On local-to-global obstructions to smoothability: in dimension 2 they vanish, for ODP’s in dimension 3 they also vanish.
There are some questions:
Q1. a) What are the smoothable normal 3-dimensional toric singularities?
There are some isolatedand some germs of non-isolated
b) What are the possible incidence relations between them?
Q2. Are local-to-global obstructions to smoothability vanish for smoothable toric singularities in dimension 3?
Q3. Show (or disprove) that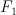 and
and 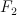 are smoothable
are smoothable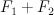 is smoothable?
is smoothable?
if
the affine singularities corresponding to the cones over
then
the affine singularity corresponding to the cone over the Minkowski sum
According to Prokhorov Q1 is open.
Answer for Q3 could be in Altmann-Straten.
I corrected a typo (343 distinct facets->344 distinct facets, twice) pointed out by Al. Sorry!