New data
I ran the Minkowski ansatz for all 4319 3-dimensional reflexive polytopes, calculating the first 100 power series coefficients of the principal period for each of them. The results were as follows.
3025 of the polytopes had a non-empty list of Minkowski polynomials, and 670 of them had more than one Minkowksi polynomial.
There were 165 distinct sequences of power series coefficients. I then looked for differential operators 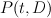 annilihating the principal period such that
annilihating the principal period such that 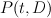 has degree
has degree  in
in  and
and  in
in 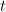 , where
, where 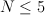 and
and 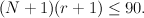 The results were:
The results were:
N=3: 23 examples in total r=2: 3 examples r=3: 2 examples r=4: 18 examples N=4: 49 examples in total r=7: 5 examples r=8: 3 examples r=9: 14 examples r=10: 27 examples N=5: 10 examples in total r=11: 1 example r=12: 2 examples r=13: 0 examples r=14: 7 examples
So in particular we found 23 D3 forms.
Tom, could you please sieve the equations (classes of polytopes with the same equation) into the following excluding categories:
1. [18 cases] Classes with a smooth toric Fano representative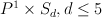
2. [+44 cases] Classes with conifold (terminal Gorenstein Fano) representative
3. [3-5 cases] Equations for
4. The rest classes/equations
1. Classes with a smooth polytope representative falls under [Givental’s theorem]:
The corresponding Fano is this representative itself.
2. Classes with a terminal Gorenstein polytope representative fall under
[Batyev’s toric degeneration ansatz/hypothesis]:
The corresponding Fano is the smoothing, it exists and can be determined by
http://member.ipmu.jp/sergey.galkin/3a.pdf (pp 11-13).
Invariants $\rho$ and $d(X)$ can be computed by
this GP script (it’s input is the coordinates of the vertices for the polytope and it’s dual).
3. Equations for
Smooth Fano varieties fall into the dichotomy: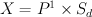 , where
, where 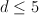
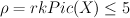
either
or
Moreover, in the case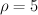 there are 3 families:
there are 3 families:
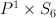 of degree 36, one other toric variety of degree 36 and one nontoric variety of degree 28 (and it admits no degenerations to terminal Gorenstein toric varieties).
of degree 36, one other toric variety of degree 36 and one nontoric variety of degree 28 (and it admits no degenerations to terminal Gorenstein toric varieties).
Del Pezzo surfaces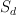 for
for 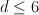 are G-Fanos.
are G-Fanos.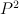 in 1 or 2 points has G-invariant Picard number equal to 2.
in 1 or 2 points has G-invariant Picard number equal to 2.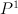 is respectively 2 or 3.
is respectively 2 or 3.
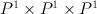 turns out to be G-Fano itself.
turns out to be G-Fano itself.
Blowup of
Hence the G-invariant Picard of their product with
So except for (possible) two cases of Fano varieties with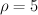
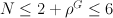 .
.
all other smooth Fano threefolds have
Since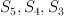 have Gorenstein degenerations, multiplied by
have Gorenstein degenerations, multiplied by 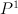 they also have Gorenstein degenerations. I am not sure whether
they also have Gorenstein degenerations. I am not sure whether 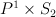 and
and 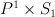 have Gorenstein degenerations.
have Gorenstein degenerations. 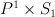 has non-free anticanonical system so probably it haven’t Gorenstein degenerations: anticanonical systems of Gorenstein Fanos are free, however the limit of the base locus for smooth threefolds may move along the singularity curve of the singular depending on the degeneration.
has non-free anticanonical system so probably it haven’t Gorenstein degenerations: anticanonical systems of Gorenstein Fanos are free, however the limit of the base locus for smooth threefolds may move along the singularity curve of the singular depending on the degeneration.
Number r looks suspiciously big.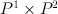 ?
?
What is r in the case of
Also, please check for the equations with N=6.
Numbers of families with the given rank of Picard group are the following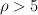 )
)
(I excluded 5 Fanos with
|------------------------------------------
| 1| 2| 3| 4|5| <=== [latex]\rho[/latex] |------------------------------------------ |17|36|31|13|3| <=== 100 smooth Fanos |------------------------------------------ | 1| 4| 7| 4|2| <=== 18 smooth toric | 4|16|16| 8|0| <=== 44 with STD |------------------------------------------ |12|16| 8| 1|1| <=== The rest -------------------------------------------
For 10 out of 12 remaining Fanos with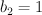 there is a Gorenstein degeneration.
there is a Gorenstein degeneration.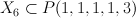 it's easy to prove - dual Gorenstein polytope should have volume 2 which is impossible.
it's easy to prove - dual Gorenstein polytope should have volume 2 which is impossible.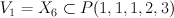 maybe one should con sider the 1/2-homothety of the dual polytope).
maybe one should con sider the 1/2-homothety of the dual polytope).
For other 2 probably there are no Gorenstein degeneration. In case of
In case of
So only a quarter of the families are left for the consideration.
Specifying some of the conventional invariants could help to furnish it further. Degree is the same for smooth and Gorenstein varieties. Upper bound of Gorenstein Picard numbers gives a lower bound for smooth Picard number.
Another question that bother me is the following:
there are 100 terminal Gorenstein polytopes and
100 of their duals (mostly non-terminal).
What Minkowski ansatz produces for these duals?