Things are not as straightforward as they seem
Consider the blow-up  of
of 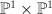 with center a complete intersection of type
with center a complete intersection of type 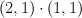 . Since the complete intersection consists of three points,
. Since the complete intersection consists of three points,  is a del Pezzo surface
is a del Pezzo surface 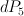 . It is tempting to compute its regularized period sequence as follows.
. It is tempting to compute its regularized period sequence as follows.
Warning: this calculation is wrong. I explain below where the error is and how to fix it. We express  as a complete intersection in a toric variety
as a complete intersection in a toric variety  as follows. Let
as follows. Let  have weight data:
have weight data:
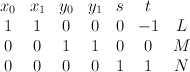
Now consider the equation:
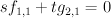
where 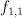 and
and 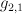 are polynomials in
are polynomials in 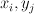 of bidegrees (respectively) (1,1) and (2,1). The variety
of bidegrees (respectively) (1,1) and (2,1). The variety  defined by this equation is cut out by a section of the line bundle
defined by this equation is cut out by a section of the line bundle 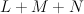 ; by projecting
; by projecting ![[x_0:x_1:y_0:y_1:s:t] \mapsto [x_0:x_1:y_0:y_1] [x_0:x_1:y_0:y_1:s:t] \mapsto [x_0:x_1:y_0:y_1]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/e81/e817d27607809e965cfe4b905bc95bc8-ffffff-000000-0.png) we see that
we see that  is, as desired, the blow-up of
is, as desired, the blow-up of 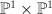 in a complete intersection of type
in a complete intersection of type 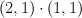 . We have
. We have 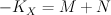 and:
and:
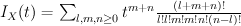
Regularizing gives the period sequence:
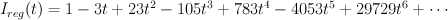
This is not correct: we know the regularized period sequences for del Pezzo surfaces, and in the case of  we get:
we get:
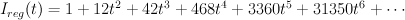
So what went wrong?
The construction of  given above is correct. It is the second half of the calculation which is flawed. The key point is that, even though
given above is correct. It is the second half of the calculation which is flawed. The key point is that, even though  is Fano and is cut out of the ambient space
is Fano and is cut out of the ambient space  by a section of an ample line bundle,
by a section of an ample line bundle, 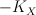 is not the restriction of an ample line bundle on
is not the restriction of an ample line bundle on  but rather is only the restriction of a semi-positive line bundle on
but rather is only the restriction of a semi-positive line bundle on  . Thus the mirror map is non-trivial. To see this we need to consider not Golyshev’s I-function:
. Thus the mirror map is non-trivial. To see this we need to consider not Golyshev’s I-function:
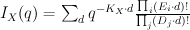
but rather the full Givental I-function:
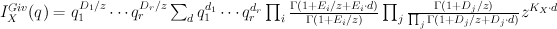
Here  is cut out of the toric variety with toric divisors
is cut out of the toric variety with toric divisors 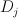 by a section of the direct sum of line bundles
by a section of the direct sum of line bundles 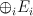 . Golyshev’s I-function is obtained from Givental’s I-function by taking the term in cohomological degree zero and setting:
. Golyshev’s I-function is obtained from Givental’s I-function by taking the term in cohomological degree zero and setting:
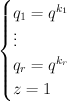
where 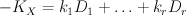 . Note that Givental’s I-function is homogeneous of degree zero if we set
. Note that Givental’s I-function is homogeneous of degree zero if we set 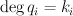 ,
, 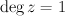 , and
, and 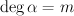 whenever
whenever 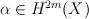 .
.
In the situation at hand (i.e.  is a semipositive complete intersection in a toric variety) we have, for grading reasons:
is a semipositive complete intersection in a toric variety) we have, for grading reasons:
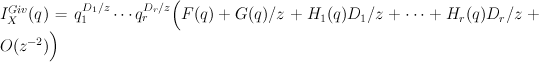
where 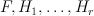 are degree-zero power series in the
are degree-zero power series in the 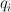 and
and 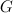 is a degree-1 power series in the
is a degree-1 power series in the 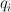 . Furthermore Givental’s mirror theorem states that:
. Furthermore Givental’s mirror theorem states that:

where:
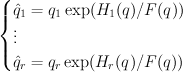
This change of variables is called the mirror map. The regularized quantum period sequence that we seek is obtained from the cohomological-degree-zero component of the J-function by setting 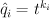 ,
, 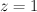 , and doing the trick with factorials:
, and doing the trick with factorials: 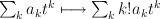 .
.
Applying this discussion in our case (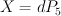 realized as above) yields:
realized as above) yields:
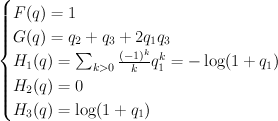
and hence:
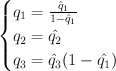
Thus the cohomological-degree-zero part of the J-function is:

and setting 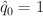 ,
, 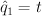 ,
, 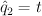 ,
, 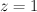 yields:
yields:
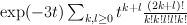
Regularizing this gives:
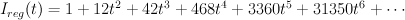
which agrees with our previous calculation.
Tom, could you please explain if the equivariant redundancy is necessary for the proper mirror map or can be ommited?
In particular, could you please write what is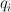 in the definition of Givental’s I-function.
in the definition of Givental’s I-function.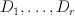 form a base for space of T-equivariant divisor classes,
form a base for space of T-equivariant divisor classes,![Formula does not parse: Pic(F) = Pic^T(F)/Hom(T,\C^*) Formula does not parse: Pic(F) = Pic^T(F)/Hom(T,\C^*)]() .
.
There is a redundancy of these parameters: divisors
but are linearly dependant in the non-equivariant Picard group:
Is d any class or a class of effective curve on and
and  ?
?
Also, variety F has an action of torus T, but complete intersection X already doesn’t admit such action.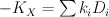 as an equation in $Pic(X)$ doesn’t define values of k_i,
as an equation in $Pic(X)$ doesn’t define values of k_i,
So
should we abandon equivariant parameters in any way and restrict ourselves to the non-equivariant only (in the example this is done indeed)?
@Sergey: is the class Poincare-dual to
is the class Poincare-dual to 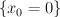 ,
, 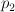 is the class Poincare-dual to
is the class Poincare-dual to 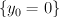 , and
, and 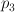 is the class Poincare-dual to
is the class Poincare-dual to 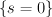 . (Thus they correspond to the standard basis when I look at the weight data defining the toric variety
. (Thus they correspond to the standard basis when I look at the weight data defining the toric variety  .)
.) 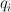 is dual to
is dual to 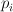 .
. 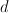 is an effective class and
is an effective class and 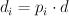 . As I see it, we do not need to consider the equivariant theory at all.
. As I see it, we do not need to consider the equivariant theory at all.