del Pezzo surfaces
Here are the G-functions (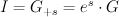 )
)
and regularized quantum periods (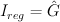 )
)
for del Pezzo surfaces.
The del Pezzo surface of degree 9
This is the toric variety  . We have:
. We have:
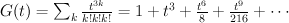
and the regularized quantum period is:
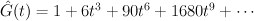
The del Pezzo surface of degree 8, case a
This is the toric variety 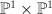 . We have:
. We have:
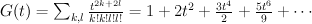
and the regularized quantum period is:
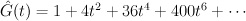
The del Pezzo surface of degree 8, case b
This is the toric variety 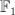 . We have:
. We have:
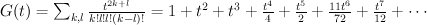
and the regularized quantum period is:
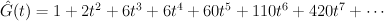
The del Pezzo surface of degree 7
This is the blow-up of  in two points. It is a toric variety. We have:
in two points. It is a toric variety. We have:
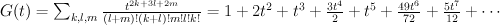
and the regularized quantum period is:
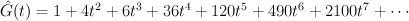
The del Pezzo surface of degree 6
This is the blow-up of  in three points. It is a toric variety. We have:
in three points. It is a toric variety. We have:
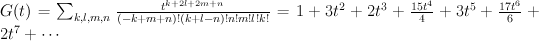
and the regularized quantum period is:
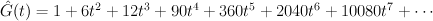
The del Pezzo surface of degree 5
This is a hypersurface of bidegree 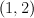 in
in  . We have:
. We have:
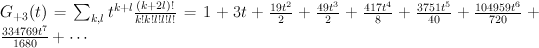
and the regularized quantum period is:
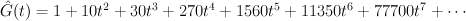
The del Pezzo surface of degree 4
This is a (2,2) complete intersection in 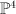 . We have:
. We have:

and the regularized quantum period is:
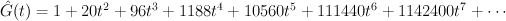
The del Pezzo surface of degree 3
This is the cubic surface in  . We have:
. We have:
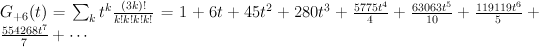
and the regularized quantum period is:
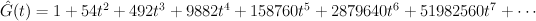
The del Pezzo surface of degree 2
This is the quartic surface in 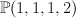 . We have:
. We have:
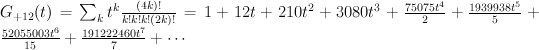
and the regularized quantum period is:
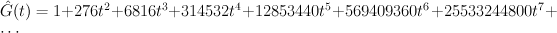
The del Pezzo surface of degree 1
This is the sextic surface in 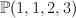 . We have:
. We have:
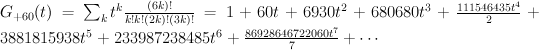
and the regularized quantum period is:
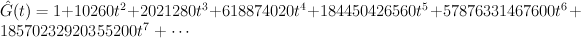
And some mirror images:
del Pezzo surfaces
Shorter forms for non-normalized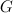 -series for del Pezzo surface of degree 6.
-series for del Pezzo surface of degree 6.
From description of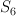 as hyperplane section of Segre threefold
as hyperplane section of Segre threefold 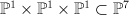 :
:
From description of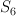 as linear section of Segre fourfold
as linear section of Segre fourfold 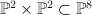 :
:
Invariant T(X) (defined in these Split notes – Definition 28) for del Pezzo surfaces equals to
Note that potentials I wrote down for del Pezzo surfaces of degrees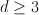 are _optimal_ – for them
are _optimal_ – for them 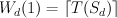 .
.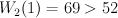 and
and  .
.
Potentials for del Pezzo surfaces of degrees 1 and 2 that I wrote down are not optimal:
Nevertheless one can obtain from them the optimal potentials by doing a relatively short sequence of mutations (using this script).
Can we beautify this page and stick it together with Fano 3-folds on top?
Done: see
http://coates.ma.ic.ac.uk/fanosearch/?page_id=5657
for the new version, which should also appear in the menu at the top of the blog.