A riddle wrapped in a mystery inside a balls-up
Consider #2 on the Mori-Mukai list of rank-3 Fano 3-folds. This has been giving us some difficulty, which I have now resolved. We were making a combination of mistakes. Mori and Mukai describe the variety  as follows.
as follows.
A member of 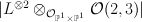 on the
on the  -bundle
-bundle  over
over 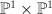 such that
such that 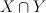 is irreducible, where
is irreducible, where  is the tautological line bundle and
is the tautological line bundle and 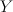 is a member of
is a member of 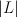 .
.
Our first mistake, as Mukai-sensei pointed out in an email to Corti, was using the wrong weight convention for projective bundles. Mori and Mukai use negative weights, so the ambient  -bundle
-bundle  is the toric variety with weight data:
is the toric variety with weight data:
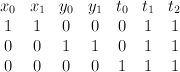
For later convenience we change basis, expressing  as the toric variety with weight data:
as the toric variety with weight data:
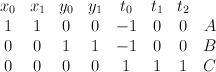
 is a section of
is a section of 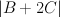 .
.
Our second mistake was failing to accurately account for the fact that although  is Fano, the bundle
is Fano, the bundle 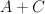 (which restricts to
(which restricts to 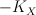 on
on  ) is only semi-positive on
) is only semi-positive on  . Thus we are in the situation described in this post and, in the notation defined there, we have:
. Thus we are in the situation described in this post and, in the notation defined there, we have:
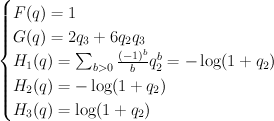
and hence:

Thus the cohomological-degree-zero part of the J-function is:

and setting 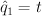 ,
, 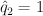 ,
, 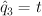 ,
, 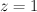 yields:
yields:
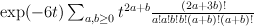
Regularizing this gives:
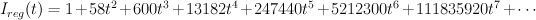
As Galkin conjectured, this is period sequence 97.