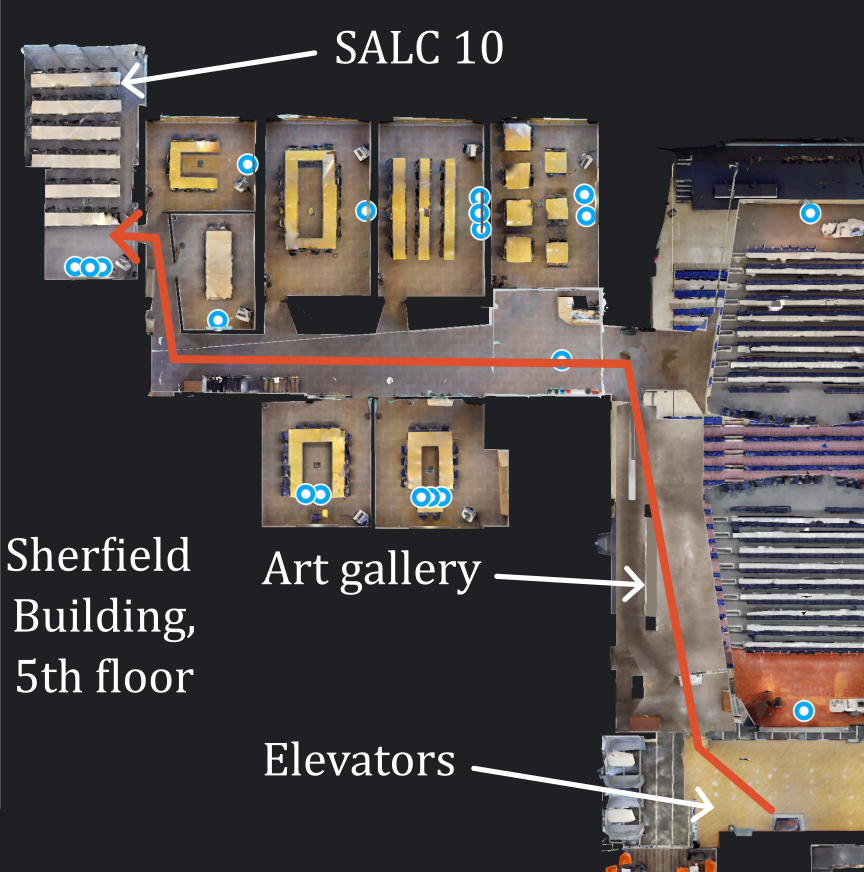
For this term, the seminars will take place in room SALC 10 (Sherfield building 5th floor, Seminar and Learning Centre room 10). The instructions below show how to reach the room:

Schedule

András Némethi (Budapest). Lattice cohomologies of normal surface singularities. Friday 9th January, 1:30-2:30pm. Huxley 144.

Abstract: The lattice cohomology associates with a geometric situation a bigraded Z[U] module. It has many different version. For example, we can define it for the topological type of a normal surface singularity (i.e. for a negative definite plumber 3-manifold), or to the analytic type of a normal surface singularity. This analytic setup can be generalized to higher dimensional isolated singularities and to
the curve case as well. The Euler characteristic of the topological lattice cohomology is the Seiberg-Witten invariant of the link (of the plumbed 3-manifold), the Euler characteristic of the analytic one is the geometric genus of the analytic germ.  (It is also known that the topological lattice cohomology is equivalent with the Heegaard Floer theory.) In the talk I will give the construction of both topological and analytical cases, I will compare them via some examples.

Cheuk Yu Mak (Sheffield). Nilpotent slices, symplectic annular Khovanov homology and fixed point localisation. Friday 16th January, 1:30-2:30pm. Sherfield, Seminar and Learning Centre 5th floor, room 10.

Abstract: Khovanov homology is a powerful link invariant which has numerous applications. In 2006, Seidel and Smith introduced a symplectic version of Khovanov homology using Lagrangians in the generic fibre of nilpotent slices. In this talk, we will first introduce a multiplicative analogue of Seidel-Smith symplectic Khovanov homology, which we call symplectic annular Khovanov homology. Then we will explain how to use it to obtain the symplectic analogue of Stoffregen-Zhang and Lipshitz-Sarkar spectral sequences relating periodic links (resp. strongly invertible knots) to their quotients. Finally, we will end with some open questions (to the best of my knowledge). This is a joint work with Hendricks and Raghunath.

Danil Kozevnikov (Edinburgh). Lagrangian skeleta of very affine complete intersections. Friday 23rd January, 1:30-2:30pm. Sherfield, Seminar and Learning Centre 5th floor, room 10.

Abstract: In this talk, I will present some new results about skeleta of complete intersections inside (C*)^n. I will start by briefly reviewing the Batyrev-Borisov mirror construction, which uses combinatorial dualities between lattice polytopes to produce mirror pairs of Calabi-Yau complete intersections in Fano toric varieties. The main focus of the talk will be open Batyrev-Borisov complete intersections (BBCIs), which are Liouville manifolds obtained by removing the toric boundary in the Batyrev-Borisov construction. I will explain how one can use tropical geometry to compute Lagrangian skeleta of open BBCIs and decompose them into pieces mirror to certain toric varieties, which leads to a proof of homological mirror symmetry (generalising the work of Gammage-Shende and Zhou in the case of hypersurfaces).

Soheyla Feyzbakhsh (Imperial). Stability conditions on Calabi-Yau threefolds via Brill-Noether theory of curves. Friday 30th January, 1:30-2:30pm. Sherfield, Seminar and Learning Centre 5th floor, room 10.

Abstract: I will explain how classical Brill–Noether theory for vector bundles on curves, which studies the number of sections of stable vector bundles, can be used to prove the Bayer–Macrì–Toda conjecture for Calabi–Yau threefolds, which guarantees the existence of Bridgeland stability conditions on them. This is joint work with Zhiyu Liu, Naoki Koseki, and Nick Rekuski. 

Graeme Wilkin (York). Loop groups, Brieskorn’s theorem and ALE spaces. Friday 6th February, 1:30-2:30pm. Sherfield, Seminar and Learning Centre 5th floor, room 10.

Abstract: Gravitational instantons are classified by the asymptotic behaviour of their metric near the boundary. In the first part of the talk I will describe joint work with Rafe Mazzeo, where we study partial compactifications of ALE gravitational instantons that have the same underlying complex manifold as the ALG gravitational instantons constructed by Hein and recently classified by Chen and Chen. In the last part of the talk I will describe work in progress to put the above construction in a more general framework and give a gauge-theoretic construction of these spaces in type A using loop groups and Brieskorn’s theorem.   

Laura Pertusi (Milan). Cubic threefolds and noncommutative curves. Friday 13th February, 1:30-2:30pm. Sherfield, Seminar and Learning Centre 5th floor, room 10.

Abstract: The bounded derived category of a cubic threefold X admits a semiorthogonal decomposition formed by two exceptional line bundles and their orthogonal complement, which we denote by Ku(X). Although stability conditions are known to exist on Ku(X), the geometric structure of the associated moduli spaces of semistable objects is rather mysterious. In this talk, I will present structure results on moduli spaces and Abel-Jacobi maps, proving some interesting analogies with moduli spaces on curves, and applications to the construction of Lagrangian subvarieties in hyperkahler manifolds. This is a joint work with Chunyi Li, Yinbang Lin and Xiaolei Zhao.

Nikolas Adaloglou (Sorbonne). Symplectomorphism groups of some rational homology balls and the Nearby Lagrangian Conjecture for their skeleta. Friday 20th February, 1:30-2:30pm. Sherfield, Seminar and Learning Centre 5th floor, room 10.

Abstract: The rational homology balls B_{p,q} are finite quotients of the Milnor fibers of the A_{p-1}-surface singularities. They have many remarkable properties as Liouville manifolds and, in particular, one can view them as the cotangent bundles of their Lagrangian skeletons, which are (non-smooth) CW-complexes, called Lagrangian L_{p,q} pinwheels. In joint work with G. Bargalló i Gómez and J. Hauber, we prove the Nearby Lagrangian Conjecture for Lagrangian L_{p,q} pinwheels: Every Lagrangian L_{p,q}-pinwheel in B_{p,q} is Hamiltonian isotopic to the standard one, namely the Lagrangian skeleton of the B_{p,q}. In this talk, after reviewing some basic facts about the B_{p,q}s and their pinwheels, I will focus on one aspect of our proof, which is the computation of the (weak) homotopy type of the compactly supported symplectomorphism group of the B_{p,q}s. In particular, I will show that every symplectomorphism is Hamiltonian isotopic to a power of a pin-twist, a Dehn-Seidel like twist around the Lagrangian skeleton.

Jordi Daura Serrano (Barcelona). Old and new results on degrees of symmetry of manifolds. Friday 27th February, 1:30-2:30pm. Sherfield, Seminar and Learning Centre 5th floor, room 10.

Abstract: Two natural questions in the theory of compact transformation groups are whether one can determine which compact Lie groups act effectively on a given manifold, and conversely, whether one can determine topological properties of a manifold if we know the compact Lie groups that act effectively on it. The second question is particularly interesting when the manifold admits actions of compact Lie groups that are “large” in a suitable sense. In the first part of the talk, we will review several invariants that make this notion of largeness precise, and we will recall known results, open questions, and conjectures related to them. In the second part, we will present answers to these questions for certain classes of manifolds, including closed connected aspherical manifolds and closed connected manifolds that fiber over the circle.

Silvia Sabatini (Cologne). Topological properties of (tall) positive monotone complexity one spaces. Friday 6th March, 1:30-2:30pm. Sherfield, Seminar and Learning Centre 5th floor, room 10.

Abstract: In symplectic geometry it is often the case that compact symplectic manifolds with large group symmetries admit indeed a Kähler structure. For instance, if the manifold is of dimension 2n and it is acted on effectively by a compact torus of dimension n in a Hamiltonian way, then it is well-known that there exists an invariant Kähler structure. These spaces are called symplectic toric manifolds or also complexity-zero spaces, where the complexity is given by half the dimension of the manifold minus the dimension of the torus acting effectively. 
In this talk I will explain how there is some evidence that a similar statement holds true when the complexity is one and the manifold is positive monotone (the latter being the symplectic analog of the Fano condition in algebraic geometry), namely, that every positive monotone complexity-one space is simply connected and has Todd genus one, properties which are also enjoyed by Fano varieties. These results are largely inspired by the Fine-Panov conjecture and are in collaboration with Daniele Sepe [2].
Moreover, with Isabelle Charton and Daniele Sepe [1], we completely classify positive monotone complexity one space that are “tall” (no reduced space is a point), and prove that the torus action extends to a full toric action, that each of these spaces admits a Kähler structure and that there are finitely many such spaces, up to a notion of equivalence that will be introduced in the talk. 

References: [1] I.Charton, S.Sabatini, D.Sepe, “Compact monotone tall complexity one T-spaces”, Transactions of the AMS, https://doi.org/10.1090/tran/9583. [2] S.Sabatini, D.Sepe, “On topological properties of positive complexity one spaces”, Transformation Groups 9  (2020).

Davide Parise (Imperial). Friday 20th March, 1:30-2:30pm. Huxley 140.