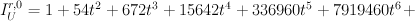PF operator:
-28672*t^4*D^3 - 172032*t^4*D^2 - 10240*t^3*D^3 - 315392*t^4*D - 46080*t^3*D^2 - 1152*t^2*D^3 - 172032*t^4 - 66560*t^3*D - 3456*t^2*D^2 - 32*t*D^3 - 30720*t^3 - 3520*t^2*D - 48*t*D^2 + D^3 - 1216*t^2 - 16*t*D
Connection matrix:
[ 0 304 9984 121088]
[ 1 16 800 9984]
[ 0 1 16 304]
[ 0 0 1 0]
This is the genus-5 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(3313, 547429), (4004, 522681), (4166, 264812), (4193, 521215), (4202, 433519), (4204, 433517), (4216, 261645), (4230, 544534), (4237, 520915), (4243, 432471), (4249, 259467), (4250, 259468), (4266, 258004), (4268, 258029), (4274, 520538), (4279, 257048), (4289, 431045), (4297, 520329), (4298, 520332), (4303, 520261), (4312, 547389), (4313, 544405), (4314, 544406)]
The corresponding toric Fanos (for each polytope) have degrees: [8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8, 8]
Each toric Fano has Hilbert series: 1 + 7*x + 25*x^2 + 63*x^3 + 129*x^4 + 231*x^5 + 377*x^6 + 575*x^7 + 833*x^8 + 1159*x^9 + 1561*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 152, 3840, 157656, 6428160, 280064960, 12618762240, 584579486680, 27660007173120, 1331176443653952, 64959370440222720, 3206739717096129984, 159854933855643586560, 8035635968276347571712, 406873893320932784947200, 20732408686051781974758360, 1062343600325163395688683520, 54705987739091805901411964480, 2829642239626465253780367452160]
==================================================
PF operator:
-128*t^4*D^3 - 768*t^4*D^2 - 1408*t^4*D - 28*t^2*D^3 - 768*t^4 - 84*t^2*D^2 - 88*t^2*D + D^3 - 32*t^2
Connection matrix:
[ 0 8 0 192]
[ 1 0 12 0]
[ 0 1 0 8]
[ 0 0 1 0]
This is a piece of the quantum cohomology of a (1,1) hypersurface in 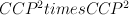 .
(This can be calculated using quantum Lefschetz.) The piece is the span of 1, K, K^2, K^3; put differently
it is the
.
(This can be calculated using quantum Lefschetz.) The piece is the span of 1, K, K^2, K^3; put differently
it is the 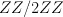 -invariant part of the cohomology under the obvious
-invariant part of the cohomology under the obvious 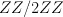 -action.
So this is a G-Fano.
This occurs for the following polytopes (PALP id, grdb id):
[(12, 544356), (21, 520158), (103, 544063), (121, 519664), (155, 430096)]
The corresponding toric Fanos (for each polytope) have degrees: [48, 48, 48, 48, 48]
Each toric Fano has Hilbert series: 1 + 27*x + 125*x^2 + 343*x^3 + 729*x^4 + 1331*x^5 + 2197*x^6 + 3375*x^7 + 4913*x^8 + 6859*x^9 + 9261*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 4, 0, 60, 0, 1120, 0, 24220, 0, 567504, 0, 14030016, 0, 360222720, 0, 9513014940, 0, 256758913840, 0]
==================================================
PF operator:
-3600*t^4*D^3 - 21600*t^4*D^2 - 2040*t^3*D^3 - 39600*t^4*D - 9180*t^3*D^2 - 359*t^2*D^3 - 21600*t^4 - 13260*t^3*D - 1077*t^2*D^2 - 14*t*D^3 - 6120*t^3 - 1102*t^2*D - 21*t*D^2 + D^3 - 384*t^2 - 7*t*D
Connection matrix:
[ 0 96 1692 12816]
[ 1 7 216 1692]
[ 0 1 7 96]
[ 0 0 1 0]
This is the genus-7 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(2755, 474429), (2816, 355616), (2816, 355616), (3405, 321303), (3446, 147470), (3446, 147470), (3451, 147467), (3504, 610803), (3504, 610803), (3624, 305807), (3625, 306072), (3666, 129112), (3682, 127896), (3701, 597737), (3730, 544886), (3761, 446913), (3790, 294031), (3790, 294031), (3794, 292940), (3795, 292458), (3843, 585895), (3843, 585895), (3844, 585890), (3844, 585890), (3845, 585897), (3845, 585897), (3847, 585514), (3852, 585548), (3856, 585686), (3867, 29624), (3867, 29624), (3868, 29628), (3873, 5953), (3873, 5953), (3874, 5954), (3874, 5954), (3932, 281846), (3935, 281906), (3936, 281910), (3937, 282088), (3945, 281909), (3961, 98314), (3965, 93823), (3966, 95245), (3980, 574886), (3982, 573895), (3983, 574977), (3984, 574842), (3990, 25067), (4026, 439663), (4042, 274128), (4057, 87167), (4057, 87167), (4058, 86668), (4059, 86880), (4069, 83883), (4074, 566716), (4074, 566716), (4075, 566695), (4075, 566695), (4079, 21153), (4101, 437078), (4103, 436976), (4118, 268997), (4121, 268912), (4123, 268019), (4132, 78482), (4133, 78269), (4143, 558361), (4144, 558688), (4148, 521504), (4168, 264855), (4168, 264855), (4169, 263867), (4178, 72123), (4179, 72493), (4181, 72684), (4181, 72684), (4182, 72202), (4182, 72202), (4183, 72680), (4217, 261497), (4219, 260624), (4240, 520890), (4246, 432558), (4248, 432464), (4253, 259203), (4262, 431807), (4269, 257760), (4271, 257945), (4272, 257862), (4292, 431027), (4293, 430976)]
The corresponding toric Fanos (for each polytope) have degrees: [12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12]
Each toric Fano has Hilbert series: 1 + 9*x + 35*x^2 + 91*x^3 + 189*x^4 + 341*x^5 + 559*x^6 + 855*x^7 + 1241*x^8 + 1729*x^9 + 2331*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 48, 600, 13176, 276480, 6259800, 146064240, 3505282200, 85882130880, 2139884768448, 54055299735360, 1381203124913304, 35635462470447840, 927068343971532048, 24292067745404178720, 640545056435479080600, 16984212847751657439360, 452567591447122633310400, 12112614406551107374960320]
==================================================
PF operator:
-80*t^4*D^3 - 480*t^4*D^2 - 136*t^3*D^3 - 880*t^4*D - 612*t^3*D^2 - 59*t^2*D^3 - 480*t^4 - 884*t^3*D - 177*t^2*D^2 - 2*t*D^3 - 408*t^3 - 182*t^2*D - 3*t*D^2 + D^3 - 64*t^2 - t*D
Connection matrix:
[ 0 16 84 336]
[ 1 1 28 84]
[ 0 1 1 16]
[ 0 0 1 0]
This is probably a G-Fano. See Galkin's example
-action.
So this is a G-Fano.
This occurs for the following polytopes (PALP id, grdb id):
[(12, 544356), (21, 520158), (103, 544063), (121, 519664), (155, 430096)]
The corresponding toric Fanos (for each polytope) have degrees: [48, 48, 48, 48, 48]
Each toric Fano has Hilbert series: 1 + 27*x + 125*x^2 + 343*x^3 + 729*x^4 + 1331*x^5 + 2197*x^6 + 3375*x^7 + 4913*x^8 + 6859*x^9 + 9261*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 4, 0, 60, 0, 1120, 0, 24220, 0, 567504, 0, 14030016, 0, 360222720, 0, 9513014940, 0, 256758913840, 0]
==================================================
PF operator:
-3600*t^4*D^3 - 21600*t^4*D^2 - 2040*t^3*D^3 - 39600*t^4*D - 9180*t^3*D^2 - 359*t^2*D^3 - 21600*t^4 - 13260*t^3*D - 1077*t^2*D^2 - 14*t*D^3 - 6120*t^3 - 1102*t^2*D - 21*t*D^2 + D^3 - 384*t^2 - 7*t*D
Connection matrix:
[ 0 96 1692 12816]
[ 1 7 216 1692]
[ 0 1 7 96]
[ 0 0 1 0]
This is the genus-7 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(2755, 474429), (2816, 355616), (2816, 355616), (3405, 321303), (3446, 147470), (3446, 147470), (3451, 147467), (3504, 610803), (3504, 610803), (3624, 305807), (3625, 306072), (3666, 129112), (3682, 127896), (3701, 597737), (3730, 544886), (3761, 446913), (3790, 294031), (3790, 294031), (3794, 292940), (3795, 292458), (3843, 585895), (3843, 585895), (3844, 585890), (3844, 585890), (3845, 585897), (3845, 585897), (3847, 585514), (3852, 585548), (3856, 585686), (3867, 29624), (3867, 29624), (3868, 29628), (3873, 5953), (3873, 5953), (3874, 5954), (3874, 5954), (3932, 281846), (3935, 281906), (3936, 281910), (3937, 282088), (3945, 281909), (3961, 98314), (3965, 93823), (3966, 95245), (3980, 574886), (3982, 573895), (3983, 574977), (3984, 574842), (3990, 25067), (4026, 439663), (4042, 274128), (4057, 87167), (4057, 87167), (4058, 86668), (4059, 86880), (4069, 83883), (4074, 566716), (4074, 566716), (4075, 566695), (4075, 566695), (4079, 21153), (4101, 437078), (4103, 436976), (4118, 268997), (4121, 268912), (4123, 268019), (4132, 78482), (4133, 78269), (4143, 558361), (4144, 558688), (4148, 521504), (4168, 264855), (4168, 264855), (4169, 263867), (4178, 72123), (4179, 72493), (4181, 72684), (4181, 72684), (4182, 72202), (4182, 72202), (4183, 72680), (4217, 261497), (4219, 260624), (4240, 520890), (4246, 432558), (4248, 432464), (4253, 259203), (4262, 431807), (4269, 257760), (4271, 257945), (4272, 257862), (4292, 431027), (4293, 430976)]
The corresponding toric Fanos (for each polytope) have degrees: [12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12]
Each toric Fano has Hilbert series: 1 + 9*x + 35*x^2 + 91*x^3 + 189*x^4 + 341*x^5 + 559*x^6 + 855*x^7 + 1241*x^8 + 1729*x^9 + 2331*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 48, 600, 13176, 276480, 6259800, 146064240, 3505282200, 85882130880, 2139884768448, 54055299735360, 1381203124913304, 35635462470447840, 927068343971532048, 24292067745404178720, 640545056435479080600, 16984212847751657439360, 452567591447122633310400, 12112614406551107374960320]
==================================================
PF operator:
-80*t^4*D^3 - 480*t^4*D^2 - 136*t^3*D^3 - 880*t^4*D - 612*t^3*D^2 - 59*t^2*D^3 - 480*t^4 - 884*t^3*D - 177*t^2*D^2 - 2*t*D^3 - 408*t^3 - 182*t^2*D - 3*t*D^2 + D^3 - 64*t^2 - t*D
Connection matrix:
[ 0 16 84 336]
[ 1 1 28 84]
[ 0 1 1 16]
[ 0 0 1 0]
This is probably a G-Fano. See Galkin's example 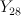 here.
here.
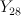 is the blow-up of a 3-dimensional quadric along a
rational normal curve of degree 4.
This occurs for the following polytopes (PALP id, grdb id):
[(122, 519649), (237, 518830), (294, 429082), (463, 543553), (512, 516974), (625, 425410), (699, 61968), (702, 61981), (730, 674688), (732, 674685), (828, 513257), (909, 420832), (917, 420911), (963, 419969), (1094, 674577), (1095, 674598), (1101, 674607), (1102, 674578), (1110, 61963), (1119, 546609), (1132, 539540), (1133, 539453), (1146, 539478), (1183, 507651), (1187, 507587), (1189, 507636), (1227, 506691), (1360, 412197), (1374, 412119), (1388, 246297), (1399, 246050), (1404, 246108), (1435, 251552), (1445, 251086), (1509, 674087), (1517, 61936), (1653, 498796), (1705, 402373), (1722, 402266), (1752, 397711), (1846, 236262), (1872, 669437), (1892, 672913), (1893, 672826), (1914, 671908), (1919, 671936), (1934, 61770), (2038, 491281), (2066, 486941), (2086, 388962), (2105, 388129), (2143, 388557), (2146, 388498), (2164, 385229), (2193, 223127), (2244, 222612), (2253, 231089), (2319, 669046), (2333, 61316), (2414, 482045), (2431, 482353), (2490, 371033), (2521, 370589), (2531, 370638), (2598, 204086), (2674, 662260), (2728, 529927), (2729, 529925), (2783, 473103), (2784, 473149), (2867, 353915), (2870, 353914), (2873, 352836), (2948, 181701), (2955, 181632), (3002, 649478), (3005, 649168), (3116, 464073), (3180, 332292), (3192, 334858), (3339, 526756), (3383, 456760), (3428, 314752), (3609, 451932), (3611, 450146), (3658, 303278), (3746, 524263)]
The corresponding toric Fanos (for each polytope) have degrees: [28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28]
Each toric Fano has Hilbert series: 1 + 17*x + 75*x^2 + 203*x^3 + 429*x^4 + 781*x^5 + 1287*x^6 + 1975*x^7 + 2873*x^8 + 4009*x^9 + 5411*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 8, 24, 240, 1440, 11960, 89040, 731920, 5913600, 49519008, 416095680, 3554134584, 30566888352, 265408469040, 2319246113184, 20400180886800, 180392364801792, 1603103294139776, 14307945541718400]
==================================================
PF operator:
-8784*t^4*D^3 - 52704*t^4*D^2 - 4080*t^3*D^3 - 96624*t^4*D - 18360*t^3*D^2 - 592*t^2*D^3 - 52704*t^4 - 26520*t^3*D - 1776*t^2*D^2 - 20*t*D^3 - 12240*t^3 - 1808*t^2*D - 30*t*D^2 + D^3 - 624*t^2 - 10*t*D
Connection matrix:
[ 0 156 3600 33120]
[ 1 10 380 3600]
[ 0 1 10 156]
[ 0 0 1 0]
This is the genus-6 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(3050, 528558), (3791, 294041), (3902, 442714), (3921, 283511), (3926, 283519), (3927, 282264), (3963, 98325), (3964, 98326), (4006, 522324), (4022, 439394), (4023, 439399), (4031, 438025), (4041, 275510), (4043, 274167), (4055, 86711), (4073, 566718), (4117, 269340), (4130, 78248), (4131, 78175), (4134, 78330), (4142, 560035), (4160, 435180), (4167, 264850), (4180, 72114), (4185, 555254), (4189, 521210), (4190, 521212), (4199, 433689), (4201, 433642), (4205, 433633), (4213, 261697), (4215, 261648), (4218, 260631), (4224, 68371), (4227, 551994), (4244, 432671), (4251, 259464), (4254, 65832), (4257, 520706), (4260, 431891), (4267, 258031), (4280, 257095), (4290, 431005), (4291, 431051), (4294, 544439), (4300, 520319), (4302, 430778), (4306, 430676), (4310, 520191)]
The corresponding toric Fanos (for each polytope) have degrees: [10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10]
Each toric Fano has Hilbert series: 1 + 8*x + 30*x^2 + 77*x^3 + 159*x^4 + 286*x^5 + 468*x^6 + 715*x^7 + 1037*x^8 + 1444*x^9 + 1946*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 78, 1320, 37746, 1051920, 31464780, 971757360, 30859805970, 1000739433120, 33005374791228, 1103665924746000, 37332067569231204, 1275110813852235360, 43916809784375982168, 1523516070448697925600, 53186807444533509802770, 1867145144587345769889600, 65871893221799542211085180, 2334228501643430357642648400]
==================================================
PF operator:
-648*t^4*D^3 - 3888*t^4*D^2 - 540*t^3*D^3 - 7128*t^4*D - 2430*t^3*D^2 - 135*t^2*D^3 - 3888*t^4 - 3510*t^3*D - 405*t^2*D^2 - 6*t*D^3 - 1620*t^3 - 414*t^2*D - 9*t*D^2 + D^3 - 144*t^2 - 3*t*D
Connection matrix:
[ 0 36 378 1944]
[ 1 3 72 378]
[ 0 1 3 36]
[ 0 0 1 0]
This is the genus-10 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(1558, 537117), (1591, 500518), (1615, 500364), (1694, 402564), (1783, 236732), (1791, 236722), (1826, 236600), (2048, 491706), (2107, 387279), (2115, 388505), (2186, 223100), (2187, 223102), (2188, 223154), (2222, 222475), (2270, 662848), (2288, 662834), (2301, 662832), (2336, 61365), (2468, 372892), (2479, 370754), (2493, 370852), (2499, 370782), (2519, 372147), (2538, 372148), (2564, 205912), (2570, 205938), (2577, 205973), (2594, 204885), (2604, 204865), (2632, 652803), (2645, 652691), (2647, 652669), (2657, 662250), (2679, 57386), (2682, 60038), (2683, 60041), (2690, 59974), (2698, 12465), (2700, 12510), (2702, 1515), (2762, 473300), (2831, 355341), (2839, 353935), (2846, 353942), (2857, 352810), (2897, 186448), (2901, 186252), (2910, 186253), (2920, 186479), (2922, 186663), (2962, 639854), (2979, 639732), (2981, 639027), (2984, 639695), (2988, 639710), (3010, 53085), (3014, 57336), (3019, 57256), (3022, 57226), (3023, 57290), (3024, 57272), (3034, 12193), (3036, 12161), (3037, 1505), (3054, 528551), (3060, 527955), (3098, 464419), (3143, 338018), (3150, 338244), (3154, 335142), (3159, 333359), (3160, 335731), (3179, 335733), (3220, 165806), (3225, 165835), (3229, 165869), (3232, 161596), (3234, 163370), (3236, 161572), (3268, 624171), (3273, 624115), (3275, 624073), (3277, 624451), (3278, 624132), (3280, 624343), (3286, 637790), (3289, 635469), (3290, 630597), (3292, 47445), (3296, 47429), (3298, 52838), (3304, 52997), (3306, 11567), (3307, 11568), (3360, 456303), (3393, 320569), (3394, 320563), (3414, 314193), (3422, 317467), (3455, 144137), (3456, 146567), (3462, 146358), (3465, 146307), (3469, 146566), (3485, 140871), (3495, 140548), (3507, 610446), (3513, 608684), (3515, 608813), (3516, 608627), (3519, 610102), (3521, 606825), (3525, 610103), (3533, 40829), (3540, 45832), (3544, 10527), (3585, 450161), (3587, 449907), (3595, 450327), (3602, 451427), (3604, 450160), (3626, 305770), (3645, 300021), (3670, 125848), (3677, 125176), (3678, 126080), (3680, 126185), (3681, 127686), (3691, 120787), (3692, 120954), (3698, 597560), (3706, 595148), (3712, 592451), (3713, 595151), (3715, 595061), (3716, 595051), (3721, 37682), (3722, 39241), (3763, 446171), (3767, 446903), (3768, 445062), (3769, 444829), (3811, 287942), (3822, 287241), (3828, 108694), (3830, 107924), (3833, 108116), (3838, 103584), (3858, 579032), (3861, 580364), (3865, 580302), (3911, 442307), (3929, 283324), (3939, 282905), (3941, 282805), (3950, 278148), (3954, 281543), (3957, 280321), (3958, 277552), (3968, 96299), (3970, 96497), (3978, 89065), (3986, 568804), (3987, 568869), (4052, 272829), (4067, 86200), (4072, 82865), (4084, 544685), (4095, 521906), (4109, 436777), (4111, 436667), (4113, 436698), (4122, 268454), (4129, 267792), (4141, 77057), (4173, 264169), (4177, 262832), (4241, 520868), (4264, 431504)]
The corresponding toric Fanos (for each polytope) have degrees: [18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18]
Each toric Fano has Hilbert series: 1 + 12*x + 50*x^2 + 133*x^3 + 279*x^4 + 506*x^5 + 832*x^6 + 1275*x^7 + 1853*x^8 + 2584*x^9 + 3486*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 18, 120, 1566, 18360, 237060, 3129840, 42576030, 590756880, 8335922868, 119226824640, 1724740692444, 25190718593040, 370964999876328, 5502056132532960, 82116488056364190, 1232339463675983520, 18584862355966240620, 281509812816269534640]
==================================================
PF operator:
-108*t^2*D^3 - 324*t^2*D^2 - 312*t^2*D + D^3 - 96*t^2
Connection matrix:
[ 0 24 0 576]
[ 1 0 60 0]
[ 0 1 0 24]
[ 0 0 1 0]
This is the cubic 3-fold
is the blow-up of a 3-dimensional quadric along a
rational normal curve of degree 4.
This occurs for the following polytopes (PALP id, grdb id):
[(122, 519649), (237, 518830), (294, 429082), (463, 543553), (512, 516974), (625, 425410), (699, 61968), (702, 61981), (730, 674688), (732, 674685), (828, 513257), (909, 420832), (917, 420911), (963, 419969), (1094, 674577), (1095, 674598), (1101, 674607), (1102, 674578), (1110, 61963), (1119, 546609), (1132, 539540), (1133, 539453), (1146, 539478), (1183, 507651), (1187, 507587), (1189, 507636), (1227, 506691), (1360, 412197), (1374, 412119), (1388, 246297), (1399, 246050), (1404, 246108), (1435, 251552), (1445, 251086), (1509, 674087), (1517, 61936), (1653, 498796), (1705, 402373), (1722, 402266), (1752, 397711), (1846, 236262), (1872, 669437), (1892, 672913), (1893, 672826), (1914, 671908), (1919, 671936), (1934, 61770), (2038, 491281), (2066, 486941), (2086, 388962), (2105, 388129), (2143, 388557), (2146, 388498), (2164, 385229), (2193, 223127), (2244, 222612), (2253, 231089), (2319, 669046), (2333, 61316), (2414, 482045), (2431, 482353), (2490, 371033), (2521, 370589), (2531, 370638), (2598, 204086), (2674, 662260), (2728, 529927), (2729, 529925), (2783, 473103), (2784, 473149), (2867, 353915), (2870, 353914), (2873, 352836), (2948, 181701), (2955, 181632), (3002, 649478), (3005, 649168), (3116, 464073), (3180, 332292), (3192, 334858), (3339, 526756), (3383, 456760), (3428, 314752), (3609, 451932), (3611, 450146), (3658, 303278), (3746, 524263)]
The corresponding toric Fanos (for each polytope) have degrees: [28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28]
Each toric Fano has Hilbert series: 1 + 17*x + 75*x^2 + 203*x^3 + 429*x^4 + 781*x^5 + 1287*x^6 + 1975*x^7 + 2873*x^8 + 4009*x^9 + 5411*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 8, 24, 240, 1440, 11960, 89040, 731920, 5913600, 49519008, 416095680, 3554134584, 30566888352, 265408469040, 2319246113184, 20400180886800, 180392364801792, 1603103294139776, 14307945541718400]
==================================================
PF operator:
-8784*t^4*D^3 - 52704*t^4*D^2 - 4080*t^3*D^3 - 96624*t^4*D - 18360*t^3*D^2 - 592*t^2*D^3 - 52704*t^4 - 26520*t^3*D - 1776*t^2*D^2 - 20*t*D^3 - 12240*t^3 - 1808*t^2*D - 30*t*D^2 + D^3 - 624*t^2 - 10*t*D
Connection matrix:
[ 0 156 3600 33120]
[ 1 10 380 3600]
[ 0 1 10 156]
[ 0 0 1 0]
This is the genus-6 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(3050, 528558), (3791, 294041), (3902, 442714), (3921, 283511), (3926, 283519), (3927, 282264), (3963, 98325), (3964, 98326), (4006, 522324), (4022, 439394), (4023, 439399), (4031, 438025), (4041, 275510), (4043, 274167), (4055, 86711), (4073, 566718), (4117, 269340), (4130, 78248), (4131, 78175), (4134, 78330), (4142, 560035), (4160, 435180), (4167, 264850), (4180, 72114), (4185, 555254), (4189, 521210), (4190, 521212), (4199, 433689), (4201, 433642), (4205, 433633), (4213, 261697), (4215, 261648), (4218, 260631), (4224, 68371), (4227, 551994), (4244, 432671), (4251, 259464), (4254, 65832), (4257, 520706), (4260, 431891), (4267, 258031), (4280, 257095), (4290, 431005), (4291, 431051), (4294, 544439), (4300, 520319), (4302, 430778), (4306, 430676), (4310, 520191)]
The corresponding toric Fanos (for each polytope) have degrees: [10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10]
Each toric Fano has Hilbert series: 1 + 8*x + 30*x^2 + 77*x^3 + 159*x^4 + 286*x^5 + 468*x^6 + 715*x^7 + 1037*x^8 + 1444*x^9 + 1946*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 78, 1320, 37746, 1051920, 31464780, 971757360, 30859805970, 1000739433120, 33005374791228, 1103665924746000, 37332067569231204, 1275110813852235360, 43916809784375982168, 1523516070448697925600, 53186807444533509802770, 1867145144587345769889600, 65871893221799542211085180, 2334228501643430357642648400]
==================================================
PF operator:
-648*t^4*D^3 - 3888*t^4*D^2 - 540*t^3*D^3 - 7128*t^4*D - 2430*t^3*D^2 - 135*t^2*D^3 - 3888*t^4 - 3510*t^3*D - 405*t^2*D^2 - 6*t*D^3 - 1620*t^3 - 414*t^2*D - 9*t*D^2 + D^3 - 144*t^2 - 3*t*D
Connection matrix:
[ 0 36 378 1944]
[ 1 3 72 378]
[ 0 1 3 36]
[ 0 0 1 0]
This is the genus-10 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(1558, 537117), (1591, 500518), (1615, 500364), (1694, 402564), (1783, 236732), (1791, 236722), (1826, 236600), (2048, 491706), (2107, 387279), (2115, 388505), (2186, 223100), (2187, 223102), (2188, 223154), (2222, 222475), (2270, 662848), (2288, 662834), (2301, 662832), (2336, 61365), (2468, 372892), (2479, 370754), (2493, 370852), (2499, 370782), (2519, 372147), (2538, 372148), (2564, 205912), (2570, 205938), (2577, 205973), (2594, 204885), (2604, 204865), (2632, 652803), (2645, 652691), (2647, 652669), (2657, 662250), (2679, 57386), (2682, 60038), (2683, 60041), (2690, 59974), (2698, 12465), (2700, 12510), (2702, 1515), (2762, 473300), (2831, 355341), (2839, 353935), (2846, 353942), (2857, 352810), (2897, 186448), (2901, 186252), (2910, 186253), (2920, 186479), (2922, 186663), (2962, 639854), (2979, 639732), (2981, 639027), (2984, 639695), (2988, 639710), (3010, 53085), (3014, 57336), (3019, 57256), (3022, 57226), (3023, 57290), (3024, 57272), (3034, 12193), (3036, 12161), (3037, 1505), (3054, 528551), (3060, 527955), (3098, 464419), (3143, 338018), (3150, 338244), (3154, 335142), (3159, 333359), (3160, 335731), (3179, 335733), (3220, 165806), (3225, 165835), (3229, 165869), (3232, 161596), (3234, 163370), (3236, 161572), (3268, 624171), (3273, 624115), (3275, 624073), (3277, 624451), (3278, 624132), (3280, 624343), (3286, 637790), (3289, 635469), (3290, 630597), (3292, 47445), (3296, 47429), (3298, 52838), (3304, 52997), (3306, 11567), (3307, 11568), (3360, 456303), (3393, 320569), (3394, 320563), (3414, 314193), (3422, 317467), (3455, 144137), (3456, 146567), (3462, 146358), (3465, 146307), (3469, 146566), (3485, 140871), (3495, 140548), (3507, 610446), (3513, 608684), (3515, 608813), (3516, 608627), (3519, 610102), (3521, 606825), (3525, 610103), (3533, 40829), (3540, 45832), (3544, 10527), (3585, 450161), (3587, 449907), (3595, 450327), (3602, 451427), (3604, 450160), (3626, 305770), (3645, 300021), (3670, 125848), (3677, 125176), (3678, 126080), (3680, 126185), (3681, 127686), (3691, 120787), (3692, 120954), (3698, 597560), (3706, 595148), (3712, 592451), (3713, 595151), (3715, 595061), (3716, 595051), (3721, 37682), (3722, 39241), (3763, 446171), (3767, 446903), (3768, 445062), (3769, 444829), (3811, 287942), (3822, 287241), (3828, 108694), (3830, 107924), (3833, 108116), (3838, 103584), (3858, 579032), (3861, 580364), (3865, 580302), (3911, 442307), (3929, 283324), (3939, 282905), (3941, 282805), (3950, 278148), (3954, 281543), (3957, 280321), (3958, 277552), (3968, 96299), (3970, 96497), (3978, 89065), (3986, 568804), (3987, 568869), (4052, 272829), (4067, 86200), (4072, 82865), (4084, 544685), (4095, 521906), (4109, 436777), (4111, 436667), (4113, 436698), (4122, 268454), (4129, 267792), (4141, 77057), (4173, 264169), (4177, 262832), (4241, 520868), (4264, 431504)]
The corresponding toric Fanos (for each polytope) have degrees: [18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18]
Each toric Fano has Hilbert series: 1 + 12*x + 50*x^2 + 133*x^3 + 279*x^4 + 506*x^5 + 832*x^6 + 1275*x^7 + 1853*x^8 + 2584*x^9 + 3486*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 18, 120, 1566, 18360, 237060, 3129840, 42576030, 590756880, 8335922868, 119226824640, 1724740692444, 25190718593040, 370964999876328, 5502056132532960, 82116488056364190, 1232339463675983520, 18584862355966240620, 281509812816269534640]
==================================================
PF operator:
-108*t^2*D^3 - 324*t^2*D^2 - 312*t^2*D + D^3 - 96*t^2
Connection matrix:
[ 0 24 0 576]
[ 1 0 60 0]
[ 0 1 0 24]
[ 0 0 1 0]
This is the cubic 3-fold 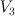 .
This occurs for the following polytopes (PALP id, grdb id):
[(231, 518837), (741, 547501)]
The corresponding toric Fanos (for each polytope) have degrees: [24, 24]
Each toric Fano has Hilbert series: 1 + 15*x + 65*x^2 + 175*x^3 + 369*x^4 + 671*x^5 + 1105*x^6 + 1695*x^7 + 2465*x^8 + 3439*x^9 + 4641*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 12, 0, 540, 0, 33600, 0, 2425500, 0, 190702512, 0, 15849497664, 0, 1369618398720, 0, 121821136479900, 0, 11079206239530000, 0]
==================================================
PF operator:
-3584*t^4*D^3 - 21504*t^4*D^2 - 2112*t^3*D^3 - 39424*t^4*D - 9504*t^3*D^2 - 368*t^2*D^3 - 21504*t^4 - 13728*t^3*D - 1104*t^2*D^2 - 12*t*D^3 - 6336*t^3 - 1088*t^2*D - 18*t*D^2 + D^3 - 352*t^2 - 6*t*D
Connection matrix:
[ 0 88 1584 11328]
[ 1 6 228 1584]
[ 0 1 6 88]
[ 0 0 1 0]
This occurs as a piece (the block 1, K, K^2, K^3) in the quantum cohomology of
a hypersurface of bidegree (2,2) in
.
This occurs for the following polytopes (PALP id, grdb id):
[(231, 518837), (741, 547501)]
The corresponding toric Fanos (for each polytope) have degrees: [24, 24]
Each toric Fano has Hilbert series: 1 + 15*x + 65*x^2 + 175*x^3 + 369*x^4 + 671*x^5 + 1105*x^6 + 1695*x^7 + 2465*x^8 + 3439*x^9 + 4641*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 12, 0, 540, 0, 33600, 0, 2425500, 0, 190702512, 0, 15849497664, 0, 1369618398720, 0, 121821136479900, 0, 11079206239530000, 0]
==================================================
PF operator:
-3584*t^4*D^3 - 21504*t^4*D^2 - 2112*t^3*D^3 - 39424*t^4*D - 9504*t^3*D^2 - 368*t^2*D^3 - 21504*t^4 - 13728*t^3*D - 1104*t^2*D^2 - 12*t*D^3 - 6336*t^3 - 1088*t^2*D - 18*t*D^2 + D^3 - 352*t^2 - 6*t*D
Connection matrix:
[ 0 88 1584 11328]
[ 1 6 228 1584]
[ 0 1 6 88]
[ 0 0 1 0]
This occurs as a piece (the block 1, K, K^2, K^3) in the quantum cohomology of
a hypersurface of bidegree (2,2) in 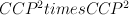 ; as before this can be calculated using
quantum Lefschetz. In particular, this is a G-Fano with
; as before this can be calculated using
quantum Lefschetz. In particular, this is a G-Fano with 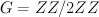 and the obvious G-action.
This occurs for the following polytopes (PALP id, grdb id):
[(2710, 530438), (2816, 355616), (3078, 466014), (3318, 545139), (3330, 526891), (3348, 525745), (3389, 321877), (3415, 317924), (3446, 147470), (3504, 610803), (3572, 452175), (3619, 306960), (3755, 446982), (3759, 446933), (3789, 294043), (3790, 294031), (3843, 585895), (3844, 585890), (3845, 585897), (3856, 585686), (3867, 29624), (3873, 5953), (3874, 5954), (3900, 442762), (3922, 283523), (3932, 281846), (3982, 573895), (4002, 522683), (4003, 522703), (4040, 275527), (4042, 274128), (4057, 87167), (4074, 566716), (4075, 566695), (4116, 269333), (4158, 435216), (4159, 434956), (4168, 264855), (4169, 263867), (4181, 72684), (4182, 72202), (4214, 261714), (4235, 544536), (4240, 520890), (4245, 432661), (4248, 432464), (4259, 431910), (4277, 431397), (4299, 520330)]
The corresponding toric Fanos (for each polytope) have degrees: [12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12]
Each toric Fano has Hilbert series: 1 + 9*x + 35*x^2 + 91*x^3 + 189*x^4 + 341*x^5 + 559*x^6 + 855*x^7 + 1241*x^8 + 1729*x^9 + 2331*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 44, 528, 11292, 228000, 4999040, 112654080, 2613620380, 61885803840, 1490373453744, 36386869189440, 898607084375616, 22407788170639872, 563420642442797568, 14268868232534243328, 363645785196486035100, 9319184268623160277632, 240004469570133005573264, 6208361451073231685966016]
==================================================
PF operator:
-256*t^4*D^3 - 1536*t^4*D^2 - 2816*t^4*D - 1536*t^4 + D^3
Connection matrix:
[ 0 0 0 256]
[ 1 0 0 0]
[ 0 1 0 0]
[ 0 0 1 0]
This is
and the obvious G-action.
This occurs for the following polytopes (PALP id, grdb id):
[(2710, 530438), (2816, 355616), (3078, 466014), (3318, 545139), (3330, 526891), (3348, 525745), (3389, 321877), (3415, 317924), (3446, 147470), (3504, 610803), (3572, 452175), (3619, 306960), (3755, 446982), (3759, 446933), (3789, 294043), (3790, 294031), (3843, 585895), (3844, 585890), (3845, 585897), (3856, 585686), (3867, 29624), (3873, 5953), (3874, 5954), (3900, 442762), (3922, 283523), (3932, 281846), (3982, 573895), (4002, 522683), (4003, 522703), (4040, 275527), (4042, 274128), (4057, 87167), (4074, 566716), (4075, 566695), (4116, 269333), (4158, 435216), (4159, 434956), (4168, 264855), (4169, 263867), (4181, 72684), (4182, 72202), (4214, 261714), (4235, 544536), (4240, 520890), (4245, 432661), (4248, 432464), (4259, 431910), (4277, 431397), (4299, 520330)]
The corresponding toric Fanos (for each polytope) have degrees: [12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12]
Each toric Fano has Hilbert series: 1 + 9*x + 35*x^2 + 91*x^3 + 189*x^4 + 341*x^5 + 559*x^6 + 855*x^7 + 1241*x^8 + 1729*x^9 + 2331*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 44, 528, 11292, 228000, 4999040, 112654080, 2613620380, 61885803840, 1490373453744, 36386869189440, 898607084375616, 22407788170639872, 563420642442797568, 14268868232534243328, 363645785196486035100, 9319184268623160277632, 240004469570133005573264, 6208361451073231685966016]
==================================================
PF operator:
-256*t^4*D^3 - 1536*t^4*D^2 - 2816*t^4*D - 1536*t^4 + D^3
Connection matrix:
[ 0 0 0 256]
[ 1 0 0 0]
[ 0 1 0 0]
[ 0 0 1 0]
This is 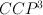 .
This occurs for the following polytopes (PALP id, grdb id):
[(0, 547386)]
The corresponding toric Fanos (for each polytope) have degrees: [64]
Each toric Fano has Hilbert series: 1 + 35*x + 165*x^2 + 455*x^3 + 969*x^4 + 1771*x^5 + 2925*x^6 + 4495*x^7 + 6545*x^8 + 9139*x^9 + 12341*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 0, 0, 24, 0, 0, 0, 2520, 0, 0, 0, 369600, 0, 0, 0, 63063000, 0, 0, 0]
==================================================
PF operator:
-192*t^3*D^3 - 864*t^3*D^2 - 80*t^2*D^3 - 1248*t^3*D - 240*t^2*D^2 - 4*t*D^3 - 576*t^3 - 256*t^2*D - 6*t*D^2 + D^3 - 96*t^2 - 2*t*D
Connection matrix:
[ 0 24 144 576]
[ 1 2 36 144]
[ 0 1 2 24]
[ 0 0 1 0]
This is a G-Fano. It occurs as the G-invariant piece (=span of 1, K, K^2, K^3) inside the quantum
cohomology of the degree (1,1,1,1) hypersurface in
.
This occurs for the following polytopes (PALP id, grdb id):
[(0, 547386)]
The corresponding toric Fanos (for each polytope) have degrees: [64]
Each toric Fano has Hilbert series: 1 + 35*x + 165*x^2 + 455*x^3 + 969*x^4 + 1771*x^5 + 2925*x^6 + 4495*x^7 + 6545*x^8 + 9139*x^9 + 12341*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 0, 0, 24, 0, 0, 0, 2520, 0, 0, 0, 369600, 0, 0, 0, 63063000, 0, 0, 0]
==================================================
PF operator:
-192*t^3*D^3 - 864*t^3*D^2 - 80*t^2*D^3 - 1248*t^3*D - 240*t^2*D^2 - 4*t*D^3 - 576*t^3 - 256*t^2*D - 6*t*D^2 + D^3 - 96*t^2 - 2*t*D
Connection matrix:
[ 0 24 144 576]
[ 1 2 36 144]
[ 0 1 2 24]
[ 0 0 1 0]
This is a G-Fano. It occurs as the G-invariant piece (=span of 1, K, K^2, K^3) inside the quantum
cohomology of the degree (1,1,1,1) hypersurface in 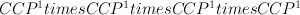 .
The group G here is the symmetric group
.
The group G here is the symmetric group 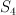 acting in the obvious way (
acting in the obvious way (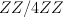 would suffice).
This occurs for the following polytopes (PALP id, grdb id):
[(488, 543412), (577, 516786), (609, 425459), (1190, 507649), (1275, 413301), (1460, 250869), (1502, 674139), (1529, 12645), (1774, 408626), (1986, 534504), (1990, 534507), (2022, 491583), (2040, 491586), (2152, 387007), (2200, 222775), (2257, 234713), (2337, 61130), (2347, 60878), (2354, 1517), (2618, 204551), (2809, 468913), (2960, 195976), (3006, 646162), (3118, 463650), (3256, 160162), (3489, 135822), (3813, 290693)]
The corresponding toric Fanos (for each polytope) have degrees: [24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24]
Each toric Fano has Hilbert series: 1 + 15*x + 65*x^2 + 175*x^3 + 369*x^4 + 671*x^5 + 1105*x^6 + 1695*x^7 + 2465*x^8 + 3439*x^9 + 4641*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 12, 48, 540, 4320, 42240, 403200, 4038300, 40958400, 423550512, 4434978240, 46982827584, 502437551616, 5417597053440, 58831951546368, 642874989479580, 7063600894137216, 77991775777488144, 864910651813116480]
==================================================
PF operator:
-336*t^4*D^3 - 2016*t^4*D^2 - 368*t^3*D^3 - 3696*t^4*D - 1656*t^3*D^2 - 112*t^2*D^3 - 2016*t^4 - 2392*t^3*D - 336*t^2*D^2 - 4*t*D^3 - 1104*t^3 - 336*t^2*D - 6*t*D^2 + D^3 - 112*t^2 - 2*t*D
Connection matrix:
[ 0 28 240 1120]
[ 1 2 60 240]
[ 0 1 2 28]
[ 0 0 1 0]
This is G-Fano
would suffice).
This occurs for the following polytopes (PALP id, grdb id):
[(488, 543412), (577, 516786), (609, 425459), (1190, 507649), (1275, 413301), (1460, 250869), (1502, 674139), (1529, 12645), (1774, 408626), (1986, 534504), (1990, 534507), (2022, 491583), (2040, 491586), (2152, 387007), (2200, 222775), (2257, 234713), (2337, 61130), (2347, 60878), (2354, 1517), (2618, 204551), (2809, 468913), (2960, 195976), (3006, 646162), (3118, 463650), (3256, 160162), (3489, 135822), (3813, 290693)]
The corresponding toric Fanos (for each polytope) have degrees: [24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24]
Each toric Fano has Hilbert series: 1 + 15*x + 65*x^2 + 175*x^3 + 369*x^4 + 671*x^5 + 1105*x^6 + 1695*x^7 + 2465*x^8 + 3439*x^9 + 4641*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 12, 48, 540, 4320, 42240, 403200, 4038300, 40958400, 423550512, 4434978240, 46982827584, 502437551616, 5417597053440, 58831951546368, 642874989479580, 7063600894137216, 77991775777488144, 864910651813116480]
==================================================
PF operator:
-336*t^4*D^3 - 2016*t^4*D^2 - 368*t^3*D^3 - 3696*t^4*D - 1656*t^3*D^2 - 112*t^2*D^3 - 2016*t^4 - 2392*t^3*D - 336*t^2*D^2 - 4*t*D^3 - 1104*t^3 - 336*t^2*D - 6*t*D^2 + D^3 - 112*t^2 - 2*t*D
Connection matrix:
[ 0 28 240 1120]
[ 1 2 60 240]
[ 0 1 2 28]
[ 0 0 1 0]
This is G-Fano 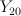 , see the comment below.
, see the comment below.
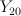 is a section of Segre variety
is a section of Segre variety 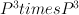 .
This occurs for the following polytopes (PALP id, grdb id):
[(1135, 539569), (1193, 507586), (1280, 413310), (1347, 413085), (1496, 674248), (1545, 537133), (1547, 537113), (1583, 500497), (1683, 402540), (1821, 236574), (1884, 672737), (1887, 672861), (2081, 388954), (2091, 388966), (2151, 388570), (2224, 222624), (2277, 662786), (2278, 662796), (2299, 662797), (2310, 668983), (2327, 61360), (2349, 12608), (2355, 10), (2411, 482428), (2480, 372136), (2539, 359406), (2548, 206001), (2579, 204760), (2643, 652681), (2653, 652715), (2665, 662262), (2681, 60032), (2688, 60031), (2697, 12519), (2721, 529907), (2742, 529800), (2748, 474431), (2761, 473110), (2780, 473340), (2819, 354967), (2820, 355397), (2889, 186748), (2915, 186256), (2954, 181697), (2974, 639652), (2975, 639467), (2995, 649245), (2999, 651604), (3009, 53121), (3028, 56368), (3076, 465966), (3089, 464399), (3133, 338175), (3134, 338158), (3200, 166803), (3253, 163000), (3270, 623294), (3302, 52267), (3336, 526335), (3354, 458626), (3401, 321330), (3420, 314336), (3439, 315731), (3477, 145166), (3494, 134327), (3500, 140258), (3524, 608931), (3539, 45839), (3551, 525020), (3590, 450075), (3603, 450158), (3633, 306075), (3668, 125301), (3704, 592333), (3774, 446837), (3805, 292773), (3860, 580376), (3892, 442983), (3979, 91442), (4014, 522631), (4016, 522644), (4027, 439692), (4176, 262193)]
The corresponding toric Fanos (for each polytope) have degrees: [20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20]
Each toric Fano has Hilbert series: 1 + 13*x + 55*x^2 + 147*x^3 + 309*x^4 + 561*x^5 + 923*x^6 + 1415*x^7 + 2057*x^8 + 2869*x^9 + 3871*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 14, 72, 882, 8400, 95180, 1060080, 12389650, 146472480, 1767391164, 21581516880, 266718438756, 3327025429728, 41849031952728, 530135326392672, 6757845419895570, 86619827323917888, 1115719258312182524, 14434274832755201424]
==================================================
PF operator:
-108*t^3*D^3 - 486*t^3*D^2 - 702*t^3*D - 324*t^3 + D^3
Connection matrix:
[ 0 0 54 0]
[ 1 0 0 54]
[ 0 1 0 0]
[ 0 0 1 0]
This is the quadric 3-fold.
This occurs for the following polytopes (PALP id, grdb id):
[(1, 547378), (3, 544395)]
The corresponding toric Fanos (for each polytope) have degrees: [54, 54]
Each toric Fano has Hilbert series: 1 + 30*x + 140*x^2 + 385*x^3 + 819*x^4 + 1496*x^5 + 2470*x^6 + 3795*x^7 + 5525*x^8 + 7714*x^9 + 10416*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 0, 12, 0, 0, 540, 0, 0, 33600, 0, 0, 2425500, 0, 0, 190702512, 0, 0, 15849497664, 0]
==================================================
PF operator:
-16*t^4*D^3 - 96*t^4*D^2 - 176*t^4*D - 44*t^2*D^3 - 96*t^4 - 132*t^2*D^2 - 136*t^2*D + D^3 - 48*t^2
Connection matrix:
[ 0 12 0 160]
[ 1 0 20 0]
[ 0 1 0 12]
[ 0 0 1 0]
This is
.
This occurs for the following polytopes (PALP id, grdb id):
[(1135, 539569), (1193, 507586), (1280, 413310), (1347, 413085), (1496, 674248), (1545, 537133), (1547, 537113), (1583, 500497), (1683, 402540), (1821, 236574), (1884, 672737), (1887, 672861), (2081, 388954), (2091, 388966), (2151, 388570), (2224, 222624), (2277, 662786), (2278, 662796), (2299, 662797), (2310, 668983), (2327, 61360), (2349, 12608), (2355, 10), (2411, 482428), (2480, 372136), (2539, 359406), (2548, 206001), (2579, 204760), (2643, 652681), (2653, 652715), (2665, 662262), (2681, 60032), (2688, 60031), (2697, 12519), (2721, 529907), (2742, 529800), (2748, 474431), (2761, 473110), (2780, 473340), (2819, 354967), (2820, 355397), (2889, 186748), (2915, 186256), (2954, 181697), (2974, 639652), (2975, 639467), (2995, 649245), (2999, 651604), (3009, 53121), (3028, 56368), (3076, 465966), (3089, 464399), (3133, 338175), (3134, 338158), (3200, 166803), (3253, 163000), (3270, 623294), (3302, 52267), (3336, 526335), (3354, 458626), (3401, 321330), (3420, 314336), (3439, 315731), (3477, 145166), (3494, 134327), (3500, 140258), (3524, 608931), (3539, 45839), (3551, 525020), (3590, 450075), (3603, 450158), (3633, 306075), (3668, 125301), (3704, 592333), (3774, 446837), (3805, 292773), (3860, 580376), (3892, 442983), (3979, 91442), (4014, 522631), (4016, 522644), (4027, 439692), (4176, 262193)]
The corresponding toric Fanos (for each polytope) have degrees: [20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20]
Each toric Fano has Hilbert series: 1 + 13*x + 55*x^2 + 147*x^3 + 309*x^4 + 561*x^5 + 923*x^6 + 1415*x^7 + 2057*x^8 + 2869*x^9 + 3871*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 14, 72, 882, 8400, 95180, 1060080, 12389650, 146472480, 1767391164, 21581516880, 266718438756, 3327025429728, 41849031952728, 530135326392672, 6757845419895570, 86619827323917888, 1115719258312182524, 14434274832755201424]
==================================================
PF operator:
-108*t^3*D^3 - 486*t^3*D^2 - 702*t^3*D - 324*t^3 + D^3
Connection matrix:
[ 0 0 54 0]
[ 1 0 0 54]
[ 0 1 0 0]
[ 0 0 1 0]
This is the quadric 3-fold.
This occurs for the following polytopes (PALP id, grdb id):
[(1, 547378), (3, 544395)]
The corresponding toric Fanos (for each polytope) have degrees: [54, 54]
Each toric Fano has Hilbert series: 1 + 30*x + 140*x^2 + 385*x^3 + 819*x^4 + 1496*x^5 + 2470*x^6 + 3795*x^7 + 5525*x^8 + 7714*x^9 + 10416*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 0, 12, 0, 0, 540, 0, 0, 33600, 0, 0, 2425500, 0, 0, 190702512, 0, 0, 15849497664, 0]
==================================================
PF operator:
-16*t^4*D^3 - 96*t^4*D^2 - 176*t^4*D - 44*t^2*D^3 - 96*t^4 - 132*t^2*D^2 - 136*t^2*D + D^3 - 48*t^2
Connection matrix:
[ 0 12 0 160]
[ 1 0 20 0]
[ 0 1 0 12]
[ 0 0 1 0]
This is 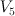 .
This occurs for the following polytopes (PALP id, grdb id):
[(42, 520063), (67, 430442), (220, 543857), (245, 518819)]
The corresponding toric Fanos (for each polytope) have degrees: [40, 40, 40, 40]
Each toric Fano has Hilbert series: 1 + 23*x + 105*x^2 + 287*x^3 + 609*x^4 + 1111*x^5 + 1833*x^6 + 2815*x^7 + 4097*x^8 + 5719*x^9 + 7721*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 6, 0, 114, 0, 2940, 0, 87570, 0, 2835756, 0, 96982116, 0, 3446781624, 0, 126047377170, 0, 4712189770860, 0]
==================================================
PF operator:
-3207168*t^4*D^3 - 19243008*t^4*D^2 - 387072*t^3*D^3 - 35278848*t^4*D - 1741824*t^3*D^2 - 14976*t^2*D^3 - 19243008*t^4 - 2515968*t^3*D - 44928*t^2*D^2 - 160*t*D^3 - 1161216*t^3 - 45504*t^2*D - 240*t*D^2 + D^3 - 15552*t^2 - 80*t*D
Connection matrix:
[ 0 3888 504576 18323712]
[ 1 80 13600 504576]
[ 0 1 80 3888]
[ 0 0 1 0]
This is the genus-3 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(4311, 547390)]
The corresponding toric Fanos (for each polytope) have degrees: [4]
Each toric Fano has Hilbert series: 1 + 5*x + 15*x^2 + 35*x^3 + 69*x^4 + 121*x^5 + 195*x^6 + 295*x^7 + 425*x^8 + 589*x^9 + 791*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 1944, 215808, 35295192, 5977566720, 1073491139520, 199954313717760, 38302652395770840, 7497487505353251840, 1493126207370030913344, 301572606517249894041600, 61627017349214878082106816, 12718722541880617724729659392, 2647214316675322606900471500288, 555025852555692350954771059458048, 117115566711982792889808392397460440, 24852125190258474673660570907685107712, 5300118106455156542190578158338402598464, 1135402757829368078738986314513572479911936]
==================================================
PF operator:
-216*t^4*D^3 - 1296*t^4*D^2 - 156*t^3*D^3 - 2376*t^4*D - 702*t^3*D^2 - 43*t^2*D^3 - 1296*t^4 - 1014*t^3*D - 129*t^2*D^2 - 2*t*D^3 - 468*t^3 - 134*t^2*D - 3*t*D^2 + D^3 - 48*t^2 - t*D
Connection matrix:
[ 0 12 90 360]
[ 1 1 20 90]
[ 0 1 1 12]
[ 0 0 1 0]
This is G-Fano: see example
.
This occurs for the following polytopes (PALP id, grdb id):
[(42, 520063), (67, 430442), (220, 543857), (245, 518819)]
The corresponding toric Fanos (for each polytope) have degrees: [40, 40, 40, 40]
Each toric Fano has Hilbert series: 1 + 23*x + 105*x^2 + 287*x^3 + 609*x^4 + 1111*x^5 + 1833*x^6 + 2815*x^7 + 4097*x^8 + 5719*x^9 + 7721*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 6, 0, 114, 0, 2940, 0, 87570, 0, 2835756, 0, 96982116, 0, 3446781624, 0, 126047377170, 0, 4712189770860, 0]
==================================================
PF operator:
-3207168*t^4*D^3 - 19243008*t^4*D^2 - 387072*t^3*D^3 - 35278848*t^4*D - 1741824*t^3*D^2 - 14976*t^2*D^3 - 19243008*t^4 - 2515968*t^3*D - 44928*t^2*D^2 - 160*t*D^3 - 1161216*t^3 - 45504*t^2*D - 240*t*D^2 + D^3 - 15552*t^2 - 80*t*D
Connection matrix:
[ 0 3888 504576 18323712]
[ 1 80 13600 504576]
[ 0 1 80 3888]
[ 0 0 1 0]
This is the genus-3 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(4311, 547390)]
The corresponding toric Fanos (for each polytope) have degrees: [4]
Each toric Fano has Hilbert series: 1 + 5*x + 15*x^2 + 35*x^3 + 69*x^4 + 121*x^5 + 195*x^6 + 295*x^7 + 425*x^8 + 589*x^9 + 791*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 1944, 215808, 35295192, 5977566720, 1073491139520, 199954313717760, 38302652395770840, 7497487505353251840, 1493126207370030913344, 301572606517249894041600, 61627017349214878082106816, 12718722541880617724729659392, 2647214316675322606900471500288, 555025852555692350954771059458048, 117115566711982792889808392397460440, 24852125190258474673660570907685107712, 5300118106455156542190578158338402598464, 1135402757829368078738986314513572479911936]
==================================================
PF operator:
-216*t^4*D^3 - 1296*t^4*D^2 - 156*t^3*D^3 - 2376*t^4*D - 702*t^3*D^2 - 43*t^2*D^3 - 1296*t^4 - 1014*t^3*D - 129*t^2*D^2 - 2*t*D^3 - 468*t^3 - 134*t^2*D - 3*t*D^2 + D^3 - 48*t^2 - t*D
Connection matrix:
[ 0 12 90 360]
[ 1 1 20 90]
[ 0 1 1 12]
[ 0 0 1 0]
This is G-Fano: see example 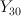 in Galkin's paper here and a comment below.
This occurs for the following polytopes (PALP id, grdb id):
[(92, 544075), (128, 519656), (369, 254882), (420, 62083), (555, 516755), (635, 425353), (736, 674673), (738, 674678), (756, 546977), (776, 541681), (801, 541398), (830, 513201), (973, 420086), (976, 420478), (981, 419971), (1042, 253678), (1062, 253974), (1084, 674626), (1104, 674529), (1234, 506708), (1295, 413098), (1497, 673893), (1507, 674094), (1523, 61915), (1764, 400494), (1766, 400145), (1767, 400227), (1811, 236421), (1851, 236231), (1853, 236555), (1858, 245022), (1913, 672076), (1933, 61769), (2030, 490916), (2175, 385001), (2240, 221492), (2321, 667186), (2442, 481366), (2450, 479732), (2504, 370044), (2528, 372132), (2529, 371259), (2610, 202555), (2797, 472610), (2882, 346002), (3068, 527903), (3176, 331526), (3188, 332295), (3440, 314609), (3787, 446396)]
The corresponding toric Fanos (for each polytope) have degrees: [30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30]
Each toric Fano has Hilbert series: 1 + 18*x + 80*x^2 + 217*x^3 + 459*x^4 + 836*x^5 + 1378*x^6 + 2115*x^7 + 3077*x^8 + 4294*x^9 + 5796*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 6, 24, 162, 1080, 7620, 55440, 415170, 3166800, 24570756, 193152960, 1535529996, 12323014704, 99702108792, 812367620064, 6660134536770, 54901225345824, 454766527525596, 3783396651070608]
==================================================
PF operator:
-304*t^4*D^3 - 1824*t^4*D^2 - 300*t^3*D^3 - 3344*t^4*D - 1350*t^3*D^2 - 88*t^2*D^3 - 1824*t^4 - 1950*t^3*D - 264*t^2*D^2 - 4*t*D^3 - 900*t^3 - 272*t^2*D - 6*t*D^2 + D^3 - 96*t^2 - 2*t*D
Connection matrix:
[ 0 24 198 880]
[ 1 2 44 198]
[ 0 1 2 24]
[ 0 0 1 0]
This is the genus-12 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(838, 513271), (929, 420909), (1021, 251679), (1027, 251680), (1140, 539490), (1271, 413299), (1312, 413150), (1427, 246241), (1481, 674247), (1483, 674241), (1603, 500036), (1699, 402281), (1715, 402297), (1721, 402434), (1785, 236692), (1815, 236477), (1854, 236595), (1879, 669463), (1885, 672886), (1886, 672906), (1888, 672877), (1897, 672700), (1898, 672887), (1900, 672881), (1928, 61779), (1929, 61780), (1936, 61803), (1941, 12639), (1942, 125), (2114, 388599), (2120, 387405), (2180, 223147), (2211, 222629), (2213, 222761), (2227, 222574), (2228, 222533), (2234, 222478), (2247, 222531), (2272, 662846), (2273, 662772), (2283, 662809), (2287, 662764), (2308, 668938), (2329, 61322), (2334, 61355), (2348, 12613), (2350, 12611), (2372, 531930), (2458, 372905), (2466, 372746), (2494, 370851), (2502, 370599), (2522, 370618), (2584, 202565), (2591, 202512), (2596, 204789), (2599, 203231), (2617, 204738), (2642, 652718), (2654, 662248), (2656, 660114), (2660, 662294), (2661, 662301), (2663, 662177), (2664, 660113), (2691, 60018), (2693, 59484), (2695, 59329), (2696, 12518), (2701, 12361), (2760, 472027), (2825, 354996), (2841, 353944), (2843, 353483), (2851, 352703), (2905, 186059), (2913, 186612), (2916, 186255), (2919, 186187), (2932, 181709), (2933, 181894), (2935, 181758), (2936, 181988), (2952, 181692), (2973, 639032), (2991, 638807), (2998, 651804), (3003, 651573), (3015, 56731), (3016, 57186), (3017, 57061), (3021, 57254), (3029, 56365), (3093, 464170), (3127, 337772), (3148, 337640), (3156, 333577), (3224, 165968), (3235, 163475), (3237, 161994), (3239, 160242), (3246, 163474), (3247, 161995), (3248, 161991), (3249, 163471), (3254, 160747), (3269, 622927), (3271, 624138), (3283, 624083), (3284, 624143), (3301, 51708), (3305, 50760), (3362, 456388), (3364, 456230), (3365, 456769), (3370, 456302), (3380, 456300), (3419, 315934), (3430, 315935), (3431, 314507), (3458, 144273), (3482, 140624), (3487, 136237), (3492, 140571), (3493, 140188), (3498, 140567), (3499, 140594), (3526, 619055), (3588, 451905), (3629, 305845), (3655, 300039), (3656, 301802), (3687, 125281), (3694, 116207), (3714, 592519), (3771, 446183), (3818, 291701), (3819, 287964), (3840, 100388), (3842, 100550), (3909, 442425), (3917, 442338), (3959, 277791), (4036, 438626), (4053, 271678), (4054, 272813), (4128, 266401), (4154, 521439)]
The corresponding toric Fanos (for each polytope) have degrees: [22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22]
Each toric Fano has Hilbert series: 1 + 14*x + 60*x^2 + 161*x^3 + 339*x^4 + 616*x^5 + 1014*x^6 + 1555*x^7 + 2261*x^8 + 3154*x^9 + 4256*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 12, 60, 636, 5760, 58620, 604800, 6447420, 70022400, 773578512, 8660892240, 98071697724, 1121159239200, 12922708539312, 150012340798320, 1752282573404220, 20581063744475520, 242914688315991120, 2879646849072124560]
==================================================
PF operator:
-256*t^2*D^3 - 768*t^2*D^2 - 704*t^2*D + D^3 - 192*t^2
Connection matrix:
[ 0 48 0 2304]
[ 1 0 160 0]
[ 0 1 0 48]
[ 0 0 1 0]
This is
in Galkin's paper here and a comment below.
This occurs for the following polytopes (PALP id, grdb id):
[(92, 544075), (128, 519656), (369, 254882), (420, 62083), (555, 516755), (635, 425353), (736, 674673), (738, 674678), (756, 546977), (776, 541681), (801, 541398), (830, 513201), (973, 420086), (976, 420478), (981, 419971), (1042, 253678), (1062, 253974), (1084, 674626), (1104, 674529), (1234, 506708), (1295, 413098), (1497, 673893), (1507, 674094), (1523, 61915), (1764, 400494), (1766, 400145), (1767, 400227), (1811, 236421), (1851, 236231), (1853, 236555), (1858, 245022), (1913, 672076), (1933, 61769), (2030, 490916), (2175, 385001), (2240, 221492), (2321, 667186), (2442, 481366), (2450, 479732), (2504, 370044), (2528, 372132), (2529, 371259), (2610, 202555), (2797, 472610), (2882, 346002), (3068, 527903), (3176, 331526), (3188, 332295), (3440, 314609), (3787, 446396)]
The corresponding toric Fanos (for each polytope) have degrees: [30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30]
Each toric Fano has Hilbert series: 1 + 18*x + 80*x^2 + 217*x^3 + 459*x^4 + 836*x^5 + 1378*x^6 + 2115*x^7 + 3077*x^8 + 4294*x^9 + 5796*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 6, 24, 162, 1080, 7620, 55440, 415170, 3166800, 24570756, 193152960, 1535529996, 12323014704, 99702108792, 812367620064, 6660134536770, 54901225345824, 454766527525596, 3783396651070608]
==================================================
PF operator:
-304*t^4*D^3 - 1824*t^4*D^2 - 300*t^3*D^3 - 3344*t^4*D - 1350*t^3*D^2 - 88*t^2*D^3 - 1824*t^4 - 1950*t^3*D - 264*t^2*D^2 - 4*t*D^3 - 900*t^3 - 272*t^2*D - 6*t*D^2 + D^3 - 96*t^2 - 2*t*D
Connection matrix:
[ 0 24 198 880]
[ 1 2 44 198]
[ 0 1 2 24]
[ 0 0 1 0]
This is the genus-12 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(838, 513271), (929, 420909), (1021, 251679), (1027, 251680), (1140, 539490), (1271, 413299), (1312, 413150), (1427, 246241), (1481, 674247), (1483, 674241), (1603, 500036), (1699, 402281), (1715, 402297), (1721, 402434), (1785, 236692), (1815, 236477), (1854, 236595), (1879, 669463), (1885, 672886), (1886, 672906), (1888, 672877), (1897, 672700), (1898, 672887), (1900, 672881), (1928, 61779), (1929, 61780), (1936, 61803), (1941, 12639), (1942, 125), (2114, 388599), (2120, 387405), (2180, 223147), (2211, 222629), (2213, 222761), (2227, 222574), (2228, 222533), (2234, 222478), (2247, 222531), (2272, 662846), (2273, 662772), (2283, 662809), (2287, 662764), (2308, 668938), (2329, 61322), (2334, 61355), (2348, 12613), (2350, 12611), (2372, 531930), (2458, 372905), (2466, 372746), (2494, 370851), (2502, 370599), (2522, 370618), (2584, 202565), (2591, 202512), (2596, 204789), (2599, 203231), (2617, 204738), (2642, 652718), (2654, 662248), (2656, 660114), (2660, 662294), (2661, 662301), (2663, 662177), (2664, 660113), (2691, 60018), (2693, 59484), (2695, 59329), (2696, 12518), (2701, 12361), (2760, 472027), (2825, 354996), (2841, 353944), (2843, 353483), (2851, 352703), (2905, 186059), (2913, 186612), (2916, 186255), (2919, 186187), (2932, 181709), (2933, 181894), (2935, 181758), (2936, 181988), (2952, 181692), (2973, 639032), (2991, 638807), (2998, 651804), (3003, 651573), (3015, 56731), (3016, 57186), (3017, 57061), (3021, 57254), (3029, 56365), (3093, 464170), (3127, 337772), (3148, 337640), (3156, 333577), (3224, 165968), (3235, 163475), (3237, 161994), (3239, 160242), (3246, 163474), (3247, 161995), (3248, 161991), (3249, 163471), (3254, 160747), (3269, 622927), (3271, 624138), (3283, 624083), (3284, 624143), (3301, 51708), (3305, 50760), (3362, 456388), (3364, 456230), (3365, 456769), (3370, 456302), (3380, 456300), (3419, 315934), (3430, 315935), (3431, 314507), (3458, 144273), (3482, 140624), (3487, 136237), (3492, 140571), (3493, 140188), (3498, 140567), (3499, 140594), (3526, 619055), (3588, 451905), (3629, 305845), (3655, 300039), (3656, 301802), (3687, 125281), (3694, 116207), (3714, 592519), (3771, 446183), (3818, 291701), (3819, 287964), (3840, 100388), (3842, 100550), (3909, 442425), (3917, 442338), (3959, 277791), (4036, 438626), (4053, 271678), (4054, 272813), (4128, 266401), (4154, 521439)]
The corresponding toric Fanos (for each polytope) have degrees: [22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22]
Each toric Fano has Hilbert series: 1 + 14*x + 60*x^2 + 161*x^3 + 339*x^4 + 616*x^5 + 1014*x^6 + 1555*x^7 + 2261*x^8 + 3154*x^9 + 4256*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 12, 60, 636, 5760, 58620, 604800, 6447420, 70022400, 773578512, 8660892240, 98071697724, 1121159239200, 12922708539312, 150012340798320, 1752282573404220, 20581063744475520, 242914688315991120, 2879646849072124560]
==================================================
PF operator:
-256*t^2*D^3 - 768*t^2*D^2 - 704*t^2*D + D^3 - 192*t^2
Connection matrix:
[ 0 48 0 2304]
[ 1 0 160 0]
[ 0 1 0 48]
[ 0 0 1 0]
This is 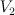 .
This occurs for the following polytopes (PALP id, grdb id):
[(427, 547520)]
The corresponding toric Fanos (for each polytope) have degrees: [16]
Each toric Fano has Hilbert series: 1 + 11*x + 45*x^2 + 119*x^3 + 249*x^4 + 451*x^5 + 741*x^6 + 1135*x^7 + 1649*x^8 + 2299*x^9 + 3101*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 24, 0, 2520, 0, 369600, 0, 63063000, 0, 11732745024, 0, 2308743493056, 0, 472518347558400, 0, 99561092450391000, 0, 21452752266265320000, 0]
==================================================
PF operator:
-1840*t^4*D^3 - 11040*t^4*D^2 - 1208*t^3*D^3 - 20240*t^4*D - 5436*t^3*D^2 - 243*t^2*D^3 - 11040*t^4 - 7852*t^3*D - 729*t^2*D^2 - 10*t*D^3 - 3624*t^3 - 742*t^2*D - 15*t*D^2 + D^3 - 256*t^2 - 5*t*D
Connection matrix:
[ 0 64 924 5936]
[ 1 5 140 924]
[ 0 1 5 64]
[ 0 0 1 0]
This is the genus-8 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(2365, 532085), (2400, 483089), (2463, 372785), (2471, 372935), (2552, 206003), (2752, 474446), (2764, 473336), (2823, 355511), (2965, 639875), (3055, 527980), (3081, 465958), (3129, 338179), (3201, 166804), (3213, 165796), (3215, 166501), (3218, 166517), (3228, 166494), (3265, 625365), (3267, 625031), (3282, 625034), (3297, 47449), (3334, 526350), (3350, 458642), (3396, 321233), (3398, 321301), (3399, 321302), (3447, 147436), (3460, 146429), (3470, 146472), (3505, 610621), (3508, 610744), (3510, 610784), (3529, 41168), (3534, 41131), (3535, 41126), (3536, 41127), (3542, 9094), (3543, 9098), (3558, 524993), (3573, 452201), (3586, 449943), (3623, 306022), (3628, 305762), (3632, 306089), (3635, 306132), (3636, 306131), (3639, 299475), (3665, 129152), (3669, 125267), (3674, 127678), (3675, 127722), (3697, 597527), (3700, 597556), (3703, 597738), (3711, 596349), (3717, 34551), (3718, 34356), (3723, 7560), (3764, 445117), (3765, 445154), (3793, 292448), (3798, 292446), (3799, 292443), (3823, 112305), (3824, 112517), (3831, 108038), (3836, 110185), (3846, 585232), (3848, 585544), (3851, 585519), (3854, 585566), (3855, 584997), (3866, 29610), (3869, 28871), (3870, 28930), (3875, 5946), (3886, 523387), (3890, 442981), (3895, 442754), (3899, 442953), (3924, 283515), (3928, 282712), (3930, 282243), (3931, 281904), (3934, 282251), (3943, 282871), (3946, 283322), (3962, 98196), (3967, 93948), (3969, 94721), (3972, 93843), (3975, 94624), (3976, 95280), (3981, 574884), (3985, 574262), (3991, 24223), (4008, 522622), (4033, 438004), (4045, 274849), (4048, 273916), (4056, 86778), (4060, 87169), (4061, 82704), (4065, 85225), (4068, 86228), (4076, 564955), (4077, 565284), (4078, 565273), (4097, 521909), (4110, 435745), (4119, 269275), (4125, 268804), (4126, 269009), (4135, 77741), (4137, 76994), (4138, 77044), (4139, 75065), (4165, 434943), (4170, 264166), (4172, 264772), (4184, 69823), (4191, 521209), (4197, 521161), (4200, 433641), (4206, 433730), (4208, 433608), (4220, 261600), (4222, 261134), (4223, 261536), (4225, 67721), (4239, 520906), (4252, 259188), (4261, 431894), (4270, 257604)]
The corresponding toric Fanos (for each polytope) have degrees: [14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14]
Each toric Fano has Hilbert series: 1 + 10*x + 40*x^2 + 105*x^3 + 219*x^4 + 396*x^5 + 650*x^6 + 995*x^7 + 1445*x^8 + 2014*x^9 + 2716*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 32, 312, 5520, 91680, 1651640, 30604560, 583436560, 11352768000, 224645958432, 4506386808000, 91434963225144, 1873214113234464, 38695098186167280, 805079741247573792, 16855708323075233040, 354862100179318727424, 7507744262279847981824, 159540694369215435619200]
==================================================
PF operator:
-165888*t^4*D^3 - 995328*t^4*D^2 - 39744*t^3*D^3 - 1824768*t^4*D - 178848*t^3*D^2 - 3024*t^2*D^3 - 995328*t^4 - 258336*t^3*D - 9072*t^2*D^2 - 60*t*D^3 - 119232*t^3 - 9216*t^2*D - 90*t*D^2 + D^3 - 3168*t^2 - 30*t*D
Connection matrix:
[ 0 792 43632 793152]
[ 1 30 2340 43632]
[ 0 1 30 792]
[ 0 0 1 0]
This is the genus-4 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(4281, 547396), (4283, 544447), (4285, 520428), (4286, 520416), (4296, 520331), (4309, 520190), (4317, 547387)]
The corresponding toric Fanos (for each polytope) have degrees: [6, 6, 6, 6, 6, 6, 6]
Each toric Fano has Hilbert series: 1 + 6*x + 20*x^2 + 49*x^3 + 99*x^4 + 176*x^5 + 286*x^6 + 435*x^7 + 629*x^8 + 874*x^9 + 1176*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 396, 17616, 1217052, 85220640, 6349812480, 490029523200, 38883641777820, 3152020367254080, 259917911904104496, 21734333812757966400, 1838661488140000620096, 157079889830458865926656, 13532851175260662410660352, 1174404851170539753963534336, 102567197002978827892527466140, 9008119389478435783966748566656, 795101313792044241851836759258896, 70492745075535384957296839185342912]
==================================================
PF operator:
-1024*t^4*D^3 - 6144*t^4*D^2 - 768*t^3*D^3 - 11264*t^4*D - 3456*t^3*D^2 - 176*t^2*D^3 - 6144*t^4 - 4992*t^3*D - 528*t^2*D^2 - 8*t*D^3 - 2304*t^3 - 544*t^2*D - 12*t*D^2 + D^3 - 192*t^2 - 4*t*D
Connection matrix:
[ 0 48 576 3328]
[ 1 4 96 576]
[ 0 1 4 48]
[ 0 0 1 0]
This is the genus-9 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(1953, 546004), (2009, 492045), (2023, 491381), (2092, 388964), (2196, 223136), (2290, 662829), (2413, 482431), (2436, 482420), (2481, 372120), (2497, 372105), (2649, 652773), (2723, 529956), (2772, 473102), (2887, 186783), (2890, 186772), (2893, 186627), (2895, 186614), (2896, 186640), (2898, 186626), (2902, 186306), (2966, 639881), (2968, 639889), (2986, 639750), (2987, 639688), (2989, 639751), (3007, 53123), (3011, 53112), (3012, 53111), (3025, 57234), (3026, 57359), (3031, 11582), (3033, 12197), (3111, 464458), (3128, 338106), (3130, 338225), (3131, 338235), (3161, 335117), (3208, 166302), (3209, 165850), (3226, 166025), (3276, 624084), (3279, 624186), (3293, 47436), (3295, 47424), (3299, 52868), (3308, 11546), (3309, 11569), (3311, 1454), (3338, 526791), (3356, 458619), (3372, 455988), (3373, 456763), (3374, 456807), (3375, 456805), (3395, 321327), (3400, 321353), (3408, 321054), (3454, 145662), (3461, 145189), (3463, 146791), (3472, 146294), (3476, 146798), (3511, 610605), (3512, 610156), (3514, 608808), (3517, 608909), (3518, 608870), (3528, 41156), (3530, 40830), (3531, 40767), (3532, 41052), (3537, 41139), (3541, 9091), (3545, 10501), (3600, 450189), (3601, 449940), (3613, 449941), (3641, 299999), (3647, 301745), (3663, 129141), (3673, 126173), (3684, 126035), (3685, 125153), (3686, 125313), (3699, 597548), (3702, 597551), (3708, 595052), (3709, 595268), (3710, 595226), (3719, 34364), (3720, 40408), (3724, 1223), (3741, 524265), (3758, 446950), (3782, 445152), (3796, 293345), (3797, 292762), (3801, 292681), (3802, 292451), (3815, 288486), (3827, 112423), (3829, 108209), (3832, 109121), (3835, 111932), (3850, 585038), (3853, 584967), (3857, 579004), (3859, 580257), (3863, 582522), (3864, 582645), (3871, 28869), (3872, 28187), (3903, 443014), (3913, 442583), (3933, 283208), (3938, 281831), (3944, 282143), (3953, 278160), (3971, 94626), (3974, 93844), (3988, 569725), (3989, 568994), (3992, 23122), (3997, 544752), (4015, 522325), (4044, 275383), (4049, 272798), (4062, 82771), (4064, 85219), (4066, 85150), (4071, 86196), (4108, 436835), (4120, 268442), (4136, 76930), (4145, 555757), (4149, 521466), (4151, 521506), (4162, 435181), (4163, 434689), (4164, 434819), (4171, 264649), (4174, 264553), (4226, 67006), (4263, 431653), (4301, 520292)]
The corresponding toric Fanos (for each polytope) have degrees: [16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16]
Each toric Fano has Hilbert series: 1 + 11*x + 45*x^2 + 119*x^3 + 249*x^4 + 451*x^5 + 741*x^6 + 1135*x^7 + 1649*x^8 + 2299*x^9 + 3101*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 24, 192, 2904, 40320, 611520, 9515520, 152412120, 2491104000, 41404233024, 697598415360, 11887922751936, 204543454123008, 3548536418059776, 62004013026988032, 1090207952792089560, 19275174299698656768, 342468223449089584704, 6111542317740696764928]
==================================================
PF operator:
144*t^4*D^3 + 864*t^4*D^2 + 1584*t^4*D - 40*t^2*D^3 + 864*t^4 - 120*t^2*D^2 - 128*t^2*D + D^3 - 48*t^2
Connection matrix:
[ 0 12 0 0]
[ 1 0 16 0]
[ 0 1 0 12]
[ 0 0 1 0]
This is
.
This occurs for the following polytopes (PALP id, grdb id):
[(427, 547520)]
The corresponding toric Fanos (for each polytope) have degrees: [16]
Each toric Fano has Hilbert series: 1 + 11*x + 45*x^2 + 119*x^3 + 249*x^4 + 451*x^5 + 741*x^6 + 1135*x^7 + 1649*x^8 + 2299*x^9 + 3101*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 24, 0, 2520, 0, 369600, 0, 63063000, 0, 11732745024, 0, 2308743493056, 0, 472518347558400, 0, 99561092450391000, 0, 21452752266265320000, 0]
==================================================
PF operator:
-1840*t^4*D^3 - 11040*t^4*D^2 - 1208*t^3*D^3 - 20240*t^4*D - 5436*t^3*D^2 - 243*t^2*D^3 - 11040*t^4 - 7852*t^3*D - 729*t^2*D^2 - 10*t*D^3 - 3624*t^3 - 742*t^2*D - 15*t*D^2 + D^3 - 256*t^2 - 5*t*D
Connection matrix:
[ 0 64 924 5936]
[ 1 5 140 924]
[ 0 1 5 64]
[ 0 0 1 0]
This is the genus-8 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(2365, 532085), (2400, 483089), (2463, 372785), (2471, 372935), (2552, 206003), (2752, 474446), (2764, 473336), (2823, 355511), (2965, 639875), (3055, 527980), (3081, 465958), (3129, 338179), (3201, 166804), (3213, 165796), (3215, 166501), (3218, 166517), (3228, 166494), (3265, 625365), (3267, 625031), (3282, 625034), (3297, 47449), (3334, 526350), (3350, 458642), (3396, 321233), (3398, 321301), (3399, 321302), (3447, 147436), (3460, 146429), (3470, 146472), (3505, 610621), (3508, 610744), (3510, 610784), (3529, 41168), (3534, 41131), (3535, 41126), (3536, 41127), (3542, 9094), (3543, 9098), (3558, 524993), (3573, 452201), (3586, 449943), (3623, 306022), (3628, 305762), (3632, 306089), (3635, 306132), (3636, 306131), (3639, 299475), (3665, 129152), (3669, 125267), (3674, 127678), (3675, 127722), (3697, 597527), (3700, 597556), (3703, 597738), (3711, 596349), (3717, 34551), (3718, 34356), (3723, 7560), (3764, 445117), (3765, 445154), (3793, 292448), (3798, 292446), (3799, 292443), (3823, 112305), (3824, 112517), (3831, 108038), (3836, 110185), (3846, 585232), (3848, 585544), (3851, 585519), (3854, 585566), (3855, 584997), (3866, 29610), (3869, 28871), (3870, 28930), (3875, 5946), (3886, 523387), (3890, 442981), (3895, 442754), (3899, 442953), (3924, 283515), (3928, 282712), (3930, 282243), (3931, 281904), (3934, 282251), (3943, 282871), (3946, 283322), (3962, 98196), (3967, 93948), (3969, 94721), (3972, 93843), (3975, 94624), (3976, 95280), (3981, 574884), (3985, 574262), (3991, 24223), (4008, 522622), (4033, 438004), (4045, 274849), (4048, 273916), (4056, 86778), (4060, 87169), (4061, 82704), (4065, 85225), (4068, 86228), (4076, 564955), (4077, 565284), (4078, 565273), (4097, 521909), (4110, 435745), (4119, 269275), (4125, 268804), (4126, 269009), (4135, 77741), (4137, 76994), (4138, 77044), (4139, 75065), (4165, 434943), (4170, 264166), (4172, 264772), (4184, 69823), (4191, 521209), (4197, 521161), (4200, 433641), (4206, 433730), (4208, 433608), (4220, 261600), (4222, 261134), (4223, 261536), (4225, 67721), (4239, 520906), (4252, 259188), (4261, 431894), (4270, 257604)]
The corresponding toric Fanos (for each polytope) have degrees: [14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14]
Each toric Fano has Hilbert series: 1 + 10*x + 40*x^2 + 105*x^3 + 219*x^4 + 396*x^5 + 650*x^6 + 995*x^7 + 1445*x^8 + 2014*x^9 + 2716*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 32, 312, 5520, 91680, 1651640, 30604560, 583436560, 11352768000, 224645958432, 4506386808000, 91434963225144, 1873214113234464, 38695098186167280, 805079741247573792, 16855708323075233040, 354862100179318727424, 7507744262279847981824, 159540694369215435619200]
==================================================
PF operator:
-165888*t^4*D^3 - 995328*t^4*D^2 - 39744*t^3*D^3 - 1824768*t^4*D - 178848*t^3*D^2 - 3024*t^2*D^3 - 995328*t^4 - 258336*t^3*D - 9072*t^2*D^2 - 60*t*D^3 - 119232*t^3 - 9216*t^2*D - 90*t*D^2 + D^3 - 3168*t^2 - 30*t*D
Connection matrix:
[ 0 792 43632 793152]
[ 1 30 2340 43632]
[ 0 1 30 792]
[ 0 0 1 0]
This is the genus-4 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(4281, 547396), (4283, 544447), (4285, 520428), (4286, 520416), (4296, 520331), (4309, 520190), (4317, 547387)]
The corresponding toric Fanos (for each polytope) have degrees: [6, 6, 6, 6, 6, 6, 6]
Each toric Fano has Hilbert series: 1 + 6*x + 20*x^2 + 49*x^3 + 99*x^4 + 176*x^5 + 286*x^6 + 435*x^7 + 629*x^8 + 874*x^9 + 1176*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 396, 17616, 1217052, 85220640, 6349812480, 490029523200, 38883641777820, 3152020367254080, 259917911904104496, 21734333812757966400, 1838661488140000620096, 157079889830458865926656, 13532851175260662410660352, 1174404851170539753963534336, 102567197002978827892527466140, 9008119389478435783966748566656, 795101313792044241851836759258896, 70492745075535384957296839185342912]
==================================================
PF operator:
-1024*t^4*D^3 - 6144*t^4*D^2 - 768*t^3*D^3 - 11264*t^4*D - 3456*t^3*D^2 - 176*t^2*D^3 - 6144*t^4 - 4992*t^3*D - 528*t^2*D^2 - 8*t*D^3 - 2304*t^3 - 544*t^2*D - 12*t*D^2 + D^3 - 192*t^2 - 4*t*D
Connection matrix:
[ 0 48 576 3328]
[ 1 4 96 576]
[ 0 1 4 48]
[ 0 0 1 0]
This is the genus-9 Fano with b_2=1.
This occurs for the following polytopes (PALP id, grdb id):
[(1953, 546004), (2009, 492045), (2023, 491381), (2092, 388964), (2196, 223136), (2290, 662829), (2413, 482431), (2436, 482420), (2481, 372120), (2497, 372105), (2649, 652773), (2723, 529956), (2772, 473102), (2887, 186783), (2890, 186772), (2893, 186627), (2895, 186614), (2896, 186640), (2898, 186626), (2902, 186306), (2966, 639881), (2968, 639889), (2986, 639750), (2987, 639688), (2989, 639751), (3007, 53123), (3011, 53112), (3012, 53111), (3025, 57234), (3026, 57359), (3031, 11582), (3033, 12197), (3111, 464458), (3128, 338106), (3130, 338225), (3131, 338235), (3161, 335117), (3208, 166302), (3209, 165850), (3226, 166025), (3276, 624084), (3279, 624186), (3293, 47436), (3295, 47424), (3299, 52868), (3308, 11546), (3309, 11569), (3311, 1454), (3338, 526791), (3356, 458619), (3372, 455988), (3373, 456763), (3374, 456807), (3375, 456805), (3395, 321327), (3400, 321353), (3408, 321054), (3454, 145662), (3461, 145189), (3463, 146791), (3472, 146294), (3476, 146798), (3511, 610605), (3512, 610156), (3514, 608808), (3517, 608909), (3518, 608870), (3528, 41156), (3530, 40830), (3531, 40767), (3532, 41052), (3537, 41139), (3541, 9091), (3545, 10501), (3600, 450189), (3601, 449940), (3613, 449941), (3641, 299999), (3647, 301745), (3663, 129141), (3673, 126173), (3684, 126035), (3685, 125153), (3686, 125313), (3699, 597548), (3702, 597551), (3708, 595052), (3709, 595268), (3710, 595226), (3719, 34364), (3720, 40408), (3724, 1223), (3741, 524265), (3758, 446950), (3782, 445152), (3796, 293345), (3797, 292762), (3801, 292681), (3802, 292451), (3815, 288486), (3827, 112423), (3829, 108209), (3832, 109121), (3835, 111932), (3850, 585038), (3853, 584967), (3857, 579004), (3859, 580257), (3863, 582522), (3864, 582645), (3871, 28869), (3872, 28187), (3903, 443014), (3913, 442583), (3933, 283208), (3938, 281831), (3944, 282143), (3953, 278160), (3971, 94626), (3974, 93844), (3988, 569725), (3989, 568994), (3992, 23122), (3997, 544752), (4015, 522325), (4044, 275383), (4049, 272798), (4062, 82771), (4064, 85219), (4066, 85150), (4071, 86196), (4108, 436835), (4120, 268442), (4136, 76930), (4145, 555757), (4149, 521466), (4151, 521506), (4162, 435181), (4163, 434689), (4164, 434819), (4171, 264649), (4174, 264553), (4226, 67006), (4263, 431653), (4301, 520292)]
The corresponding toric Fanos (for each polytope) have degrees: [16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16]
Each toric Fano has Hilbert series: 1 + 11*x + 45*x^2 + 119*x^3 + 249*x^4 + 451*x^5 + 741*x^6 + 1135*x^7 + 1649*x^8 + 2299*x^9 + 3101*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 24, 192, 2904, 40320, 611520, 9515520, 152412120, 2491104000, 41404233024, 697598415360, 11887922751936, 204543454123008, 3548536418059776, 62004013026988032, 1090207952792089560, 19275174299698656768, 342468223449089584704, 6111542317740696764928]
==================================================
PF operator:
144*t^4*D^3 + 864*t^4*D^2 + 1584*t^4*D - 40*t^2*D^3 + 864*t^4 - 120*t^2*D^2 - 128*t^2*D + D^3 - 48*t^2
Connection matrix:
[ 0 12 0 0]
[ 1 0 16 0]
[ 0 1 0 12]
[ 0 0 1 0]
This is 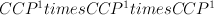 .
This occurs for the following polytopes (PALP id, grdb id):
[(17, 544342), (30, 520140), (121, 519664), (155, 430096)]
The corresponding toric Fanos (for each polytope) have degrees: [48, 48, 48, 48]
Each toric Fano has Hilbert series: 1 + 27*x + 125*x^2 + 343*x^3 + 729*x^4 + 1331*x^5 + 2197*x^6 + 3375*x^7 + 4913*x^8 + 6859*x^9 + 9261*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 6, 0, 90, 0, 1860, 0, 44730, 0, 1172556, 0, 32496156, 0, 936369720, 0, 27770358330, 0, 842090474940, 0]
==================================================
PF operator:
-2160*t^4*D^3 - 12960*t^4*D^2 - 1728*t^3*D^3 - 23760*t^4*D - 7776*t^3*D^2 - 360*t^2*D^3 - 12960*t^4 - 11232*t^3*D - 1080*t^2*D^2 - 16*t*D^3 - 5184*t^3 - 1152*t^2*D - 24*t*D^2 + D^3 - 432*t^2 - 8*t*D
Connection matrix:
[ 0 108 1728 13824]
[ 1 8 208 1728]
[ 0 1 8 108]
[ 0 0 1 0]
??? currently unknown: conjecturally a G-Fano, arising as a piece of the quantum cohomology of
a 2:1 cover of
.
This occurs for the following polytopes (PALP id, grdb id):
[(17, 544342), (30, 520140), (121, 519664), (155, 430096)]
The corresponding toric Fanos (for each polytope) have degrees: [48, 48, 48, 48]
Each toric Fano has Hilbert series: 1 + 27*x + 125*x^2 + 343*x^3 + 729*x^4 + 1331*x^5 + 2197*x^6 + 3375*x^7 + 4913*x^8 + 6859*x^9 + 9261*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 6, 0, 90, 0, 1860, 0, 44730, 0, 1172556, 0, 32496156, 0, 936369720, 0, 27770358330, 0, 842090474940, 0]
==================================================
PF operator:
-2160*t^4*D^3 - 12960*t^4*D^2 - 1728*t^3*D^3 - 23760*t^4*D - 7776*t^3*D^2 - 360*t^2*D^3 - 12960*t^4 - 11232*t^3*D - 1080*t^2*D^2 - 16*t*D^3 - 5184*t^3 - 1152*t^2*D - 24*t*D^2 + D^3 - 432*t^2 - 8*t*D
Connection matrix:
[ 0 108 1728 13824]
[ 1 8 208 1728]
[ 0 1 8 108]
[ 0 0 1 0]
??? currently unknown: conjecturally a G-Fano, arising as a piece of the quantum cohomology of
a 2:1 cover of 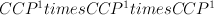 branched over a (2,2,2) hypersurface.
This occurs for the following polytopes (PALP id, grdb id):
[(2816, 355616), (3328, 545072), (3349, 525553), (3392, 321879), (3446, 147470), (3504, 610803), (3739, 524375), (3790, 294031), (3794, 292940), (3843, 585895), (3844, 585890), (3845, 585897), (3867, 29624), (3873, 5953), (3874, 5954), (3966, 95245), (4026, 439663), (4057, 87167), (4074, 566716), (4075, 566695), (4168, 264855), (4181, 72684), (4182, 72202), (4240, 520890), (4248, 432464)]
The corresponding toric Fanos (for each polytope) have degrees: [12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12]
Each toric Fano has Hilbert series: 1 + 9*x + 35*x^2 + 91*x^3 + 189*x^4 + 341*x^5 + 559*x^6 + 855*x^7 + 1241*x^8 + 1729*x^9 + 2331*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 54, 672, 15642, 336960, 7919460, 191177280, 4751272890, 120527514240, 3109617573804, 81336932550720, 2152021034457756, 57492903382282368, 1548779408915134968, 42023349488330001792, 1147430010272379786810, 31504595489224640310528, 869291145239891056320924, 24092072648449534765168704]
==================================================
PF operator:
-64*t^2*D^3 - 192*t^2*D^2 - 192*t^2*D + D^3 - 64*t^2
Connection matrix:
[ 0 16 0 256]
[ 1 0 32 0]
[ 0 1 0 16]
[ 0 0 1 0]
This is
branched over a (2,2,2) hypersurface.
This occurs for the following polytopes (PALP id, grdb id):
[(2816, 355616), (3328, 545072), (3349, 525553), (3392, 321879), (3446, 147470), (3504, 610803), (3739, 524375), (3790, 294031), (3794, 292940), (3843, 585895), (3844, 585890), (3845, 585897), (3867, 29624), (3873, 5953), (3874, 5954), (3966, 95245), (4026, 439663), (4057, 87167), (4074, 566716), (4075, 566695), (4168, 264855), (4181, 72684), (4182, 72202), (4240, 520890), (4248, 432464)]
The corresponding toric Fanos (for each polytope) have degrees: [12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12]
Each toric Fano has Hilbert series: 1 + 9*x + 35*x^2 + 91*x^3 + 189*x^4 + 341*x^5 + 559*x^6 + 855*x^7 + 1241*x^8 + 1729*x^9 + 2331*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 54, 672, 15642, 336960, 7919460, 191177280, 4751272890, 120527514240, 3109617573804, 81336932550720, 2152021034457756, 57492903382282368, 1548779408915134968, 42023349488330001792, 1147430010272379786810, 31504595489224640310528, 869291145239891056320924, 24092072648449534765168704]
==================================================
PF operator:
-64*t^2*D^3 - 192*t^2*D^2 - 192*t^2*D + D^3 - 64*t^2
Connection matrix:
[ 0 16 0 256]
[ 1 0 32 0]
[ 0 1 0 16]
[ 0 0 1 0]
This is 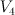 .
This occurs for the following polytopes (PALP id, grdb id):
[(8, 547367), (91, 544065), (119, 519672), (153, 430103), (197, 255744), (428, 547516), (432, 547285), (433, 547298)]
The corresponding toric Fanos (for each polytope) have degrees: [32, 32, 32, 32, 32, 32, 32, 32]
Each toric Fano has Hilbert series: 1 + 19*x + 85*x^2 + 231*x^3 + 489*x^4 + 891*x^5 + 1469*x^6 + 2255*x^7 + 3281*x^8 + 4579*x^9 + 6181*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 8, 0, 216, 0, 8000, 0, 343000, 0, 16003008, 0, 788889024, 0, 40424237568, 0, 2131746903000, 0, 114933031928000, 0]
==================================================
.
This occurs for the following polytopes (PALP id, grdb id):
[(8, 547367), (91, 544065), (119, 519672), (153, 430103), (197, 255744), (428, 547516), (432, 547285), (433, 547298)]
The corresponding toric Fanos (for each polytope) have degrees: [32, 32, 32, 32, 32, 32, 32, 32]
Each toric Fano has Hilbert series: 1 + 19*x + 85*x^2 + 231*x^3 + 489*x^4 + 891*x^5 + 1469*x^6 + 2255*x^7 + 3281*x^8 + 4579*x^9 + 6181*x^10 + O(x^11)
The first 20 coefficients of the period are:
[1, 0, 8, 0, 216, 0, 8000, 0, 343000, 0, 16003008, 0, 788889024, 0, 40424237568, 0, 2131746903000, 0, 114933031928000, 0]
==================================================
. (This can be calculated using quantum Lefschetz.) The piece is the span of 1, K, K^2, K^3; put differently it is the
-invariant part of the cohomology under the obvious
-action. So this is a G-Fano. This occurs for the following polytopes (PALP id, grdb id): [(12, 544356), (21, 520158), (103, 544063), (121, 519664), (155, 430096)] The corresponding toric Fanos (for each polytope) have degrees: [48, 48, 48, 48, 48] Each toric Fano has Hilbert series: 1 + 27*x + 125*x^2 + 343*x^3 + 729*x^4 + 1331*x^5 + 2197*x^6 + 3375*x^7 + 4913*x^8 + 6859*x^9 + 9261*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 4, 0, 60, 0, 1120, 0, 24220, 0, 567504, 0, 14030016, 0, 360222720, 0, 9513014940, 0, 256758913840, 0] ================================================== PF operator: -3600*t^4*D^3 - 21600*t^4*D^2 - 2040*t^3*D^3 - 39600*t^4*D - 9180*t^3*D^2 - 359*t^2*D^3 - 21600*t^4 - 13260*t^3*D - 1077*t^2*D^2 - 14*t*D^3 - 6120*t^3 - 1102*t^2*D - 21*t*D^2 + D^3 - 384*t^2 - 7*t*D Connection matrix: [ 0 96 1692 12816] [ 1 7 216 1692] [ 0 1 7 96] [ 0 0 1 0] This is the genus-7 Fano with b_2=1. This occurs for the following polytopes (PALP id, grdb id): [(2755, 474429), (2816, 355616), (2816, 355616), (3405, 321303), (3446, 147470), (3446, 147470), (3451, 147467), (3504, 610803), (3504, 610803), (3624, 305807), (3625, 306072), (3666, 129112), (3682, 127896), (3701, 597737), (3730, 544886), (3761, 446913), (3790, 294031), (3790, 294031), (3794, 292940), (3795, 292458), (3843, 585895), (3843, 585895), (3844, 585890), (3844, 585890), (3845, 585897), (3845, 585897), (3847, 585514), (3852, 585548), (3856, 585686), (3867, 29624), (3867, 29624), (3868, 29628), (3873, 5953), (3873, 5953), (3874, 5954), (3874, 5954), (3932, 281846), (3935, 281906), (3936, 281910), (3937, 282088), (3945, 281909), (3961, 98314), (3965, 93823), (3966, 95245), (3980, 574886), (3982, 573895), (3983, 574977), (3984, 574842), (3990, 25067), (4026, 439663), (4042, 274128), (4057, 87167), (4057, 87167), (4058, 86668), (4059, 86880), (4069, 83883), (4074, 566716), (4074, 566716), (4075, 566695), (4075, 566695), (4079, 21153), (4101, 437078), (4103, 436976), (4118, 268997), (4121, 268912), (4123, 268019), (4132, 78482), (4133, 78269), (4143, 558361), (4144, 558688), (4148, 521504), (4168, 264855), (4168, 264855), (4169, 263867), (4178, 72123), (4179, 72493), (4181, 72684), (4181, 72684), (4182, 72202), (4182, 72202), (4183, 72680), (4217, 261497), (4219, 260624), (4240, 520890), (4246, 432558), (4248, 432464), (4253, 259203), (4262, 431807), (4269, 257760), (4271, 257945), (4272, 257862), (4292, 431027), (4293, 430976)] The corresponding toric Fanos (for each polytope) have degrees: [12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12] Each toric Fano has Hilbert series: 1 + 9*x + 35*x^2 + 91*x^3 + 189*x^4 + 341*x^5 + 559*x^6 + 855*x^7 + 1241*x^8 + 1729*x^9 + 2331*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 48, 600, 13176, 276480, 6259800, 146064240, 3505282200, 85882130880, 2139884768448, 54055299735360, 1381203124913304, 35635462470447840, 927068343971532048, 24292067745404178720, 640545056435479080600, 16984212847751657439360, 452567591447122633310400, 12112614406551107374960320] ================================================== PF operator: -80*t^4*D^3 - 480*t^4*D^2 - 136*t^3*D^3 - 880*t^4*D - 612*t^3*D^2 - 59*t^2*D^3 - 480*t^4 - 884*t^3*D - 177*t^2*D^2 - 2*t*D^3 - 408*t^3 - 182*t^2*D - 3*t*D^2 + D^3 - 64*t^2 - t*D Connection matrix: [ 0 16 84 336] [ 1 1 28 84] [ 0 1 1 16] [ 0 0 1 0] This is probably a G-Fano. See Galkin's example
here.
is the blow-up of a 3-dimensional quadric along a rational normal curve of degree 4. This occurs for the following polytopes (PALP id, grdb id): [(122, 519649), (237, 518830), (294, 429082), (463, 543553), (512, 516974), (625, 425410), (699, 61968), (702, 61981), (730, 674688), (732, 674685), (828, 513257), (909, 420832), (917, 420911), (963, 419969), (1094, 674577), (1095, 674598), (1101, 674607), (1102, 674578), (1110, 61963), (1119, 546609), (1132, 539540), (1133, 539453), (1146, 539478), (1183, 507651), (1187, 507587), (1189, 507636), (1227, 506691), (1360, 412197), (1374, 412119), (1388, 246297), (1399, 246050), (1404, 246108), (1435, 251552), (1445, 251086), (1509, 674087), (1517, 61936), (1653, 498796), (1705, 402373), (1722, 402266), (1752, 397711), (1846, 236262), (1872, 669437), (1892, 672913), (1893, 672826), (1914, 671908), (1919, 671936), (1934, 61770), (2038, 491281), (2066, 486941), (2086, 388962), (2105, 388129), (2143, 388557), (2146, 388498), (2164, 385229), (2193, 223127), (2244, 222612), (2253, 231089), (2319, 669046), (2333, 61316), (2414, 482045), (2431, 482353), (2490, 371033), (2521, 370589), (2531, 370638), (2598, 204086), (2674, 662260), (2728, 529927), (2729, 529925), (2783, 473103), (2784, 473149), (2867, 353915), (2870, 353914), (2873, 352836), (2948, 181701), (2955, 181632), (3002, 649478), (3005, 649168), (3116, 464073), (3180, 332292), (3192, 334858), (3339, 526756), (3383, 456760), (3428, 314752), (3609, 451932), (3611, 450146), (3658, 303278), (3746, 524263)] The corresponding toric Fanos (for each polytope) have degrees: [28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28, 28] Each toric Fano has Hilbert series: 1 + 17*x + 75*x^2 + 203*x^3 + 429*x^4 + 781*x^5 + 1287*x^6 + 1975*x^7 + 2873*x^8 + 4009*x^9 + 5411*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 8, 24, 240, 1440, 11960, 89040, 731920, 5913600, 49519008, 416095680, 3554134584, 30566888352, 265408469040, 2319246113184, 20400180886800, 180392364801792, 1603103294139776, 14307945541718400] ================================================== PF operator: -8784*t^4*D^3 - 52704*t^4*D^2 - 4080*t^3*D^3 - 96624*t^4*D - 18360*t^3*D^2 - 592*t^2*D^3 - 52704*t^4 - 26520*t^3*D - 1776*t^2*D^2 - 20*t*D^3 - 12240*t^3 - 1808*t^2*D - 30*t*D^2 + D^3 - 624*t^2 - 10*t*D Connection matrix: [ 0 156 3600 33120] [ 1 10 380 3600] [ 0 1 10 156] [ 0 0 1 0] This is the genus-6 Fano with b_2=1. This occurs for the following polytopes (PALP id, grdb id): [(3050, 528558), (3791, 294041), (3902, 442714), (3921, 283511), (3926, 283519), (3927, 282264), (3963, 98325), (3964, 98326), (4006, 522324), (4022, 439394), (4023, 439399), (4031, 438025), (4041, 275510), (4043, 274167), (4055, 86711), (4073, 566718), (4117, 269340), (4130, 78248), (4131, 78175), (4134, 78330), (4142, 560035), (4160, 435180), (4167, 264850), (4180, 72114), (4185, 555254), (4189, 521210), (4190, 521212), (4199, 433689), (4201, 433642), (4205, 433633), (4213, 261697), (4215, 261648), (4218, 260631), (4224, 68371), (4227, 551994), (4244, 432671), (4251, 259464), (4254, 65832), (4257, 520706), (4260, 431891), (4267, 258031), (4280, 257095), (4290, 431005), (4291, 431051), (4294, 544439), (4300, 520319), (4302, 430778), (4306, 430676), (4310, 520191)] The corresponding toric Fanos (for each polytope) have degrees: [10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10, 10] Each toric Fano has Hilbert series: 1 + 8*x + 30*x^2 + 77*x^3 + 159*x^4 + 286*x^5 + 468*x^6 + 715*x^7 + 1037*x^8 + 1444*x^9 + 1946*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 78, 1320, 37746, 1051920, 31464780, 971757360, 30859805970, 1000739433120, 33005374791228, 1103665924746000, 37332067569231204, 1275110813852235360, 43916809784375982168, 1523516070448697925600, 53186807444533509802770, 1867145144587345769889600, 65871893221799542211085180, 2334228501643430357642648400] ================================================== PF operator: -648*t^4*D^3 - 3888*t^4*D^2 - 540*t^3*D^3 - 7128*t^4*D - 2430*t^3*D^2 - 135*t^2*D^3 - 3888*t^4 - 3510*t^3*D - 405*t^2*D^2 - 6*t*D^3 - 1620*t^3 - 414*t^2*D - 9*t*D^2 + D^3 - 144*t^2 - 3*t*D Connection matrix: [ 0 36 378 1944] [ 1 3 72 378] [ 0 1 3 36] [ 0 0 1 0] This is the genus-10 Fano with b_2=1. This occurs for the following polytopes (PALP id, grdb id): [(1558, 537117), (1591, 500518), (1615, 500364), (1694, 402564), (1783, 236732), (1791, 236722), (1826, 236600), (2048, 491706), (2107, 387279), (2115, 388505), (2186, 223100), (2187, 223102), (2188, 223154), (2222, 222475), (2270, 662848), (2288, 662834), (2301, 662832), (2336, 61365), (2468, 372892), (2479, 370754), (2493, 370852), (2499, 370782), (2519, 372147), (2538, 372148), (2564, 205912), (2570, 205938), (2577, 205973), (2594, 204885), (2604, 204865), (2632, 652803), (2645, 652691), (2647, 652669), (2657, 662250), (2679, 57386), (2682, 60038), (2683, 60041), (2690, 59974), (2698, 12465), (2700, 12510), (2702, 1515), (2762, 473300), (2831, 355341), (2839, 353935), (2846, 353942), (2857, 352810), (2897, 186448), (2901, 186252), (2910, 186253), (2920, 186479), (2922, 186663), (2962, 639854), (2979, 639732), (2981, 639027), (2984, 639695), (2988, 639710), (3010, 53085), (3014, 57336), (3019, 57256), (3022, 57226), (3023, 57290), (3024, 57272), (3034, 12193), (3036, 12161), (3037, 1505), (3054, 528551), (3060, 527955), (3098, 464419), (3143, 338018), (3150, 338244), (3154, 335142), (3159, 333359), (3160, 335731), (3179, 335733), (3220, 165806), (3225, 165835), (3229, 165869), (3232, 161596), (3234, 163370), (3236, 161572), (3268, 624171), (3273, 624115), (3275, 624073), (3277, 624451), (3278, 624132), (3280, 624343), (3286, 637790), (3289, 635469), (3290, 630597), (3292, 47445), (3296, 47429), (3298, 52838), (3304, 52997), (3306, 11567), (3307, 11568), (3360, 456303), (3393, 320569), (3394, 320563), (3414, 314193), (3422, 317467), (3455, 144137), (3456, 146567), (3462, 146358), (3465, 146307), (3469, 146566), (3485, 140871), (3495, 140548), (3507, 610446), (3513, 608684), (3515, 608813), (3516, 608627), (3519, 610102), (3521, 606825), (3525, 610103), (3533, 40829), (3540, 45832), (3544, 10527), (3585, 450161), (3587, 449907), (3595, 450327), (3602, 451427), (3604, 450160), (3626, 305770), (3645, 300021), (3670, 125848), (3677, 125176), (3678, 126080), (3680, 126185), (3681, 127686), (3691, 120787), (3692, 120954), (3698, 597560), (3706, 595148), (3712, 592451), (3713, 595151), (3715, 595061), (3716, 595051), (3721, 37682), (3722, 39241), (3763, 446171), (3767, 446903), (3768, 445062), (3769, 444829), (3811, 287942), (3822, 287241), (3828, 108694), (3830, 107924), (3833, 108116), (3838, 103584), (3858, 579032), (3861, 580364), (3865, 580302), (3911, 442307), (3929, 283324), (3939, 282905), (3941, 282805), (3950, 278148), (3954, 281543), (3957, 280321), (3958, 277552), (3968, 96299), (3970, 96497), (3978, 89065), (3986, 568804), (3987, 568869), (4052, 272829), (4067, 86200), (4072, 82865), (4084, 544685), (4095, 521906), (4109, 436777), (4111, 436667), (4113, 436698), (4122, 268454), (4129, 267792), (4141, 77057), (4173, 264169), (4177, 262832), (4241, 520868), (4264, 431504)] The corresponding toric Fanos (for each polytope) have degrees: [18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18, 18] Each toric Fano has Hilbert series: 1 + 12*x + 50*x^2 + 133*x^3 + 279*x^4 + 506*x^5 + 832*x^6 + 1275*x^7 + 1853*x^8 + 2584*x^9 + 3486*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 18, 120, 1566, 18360, 237060, 3129840, 42576030, 590756880, 8335922868, 119226824640, 1724740692444, 25190718593040, 370964999876328, 5502056132532960, 82116488056364190, 1232339463675983520, 18584862355966240620, 281509812816269534640] ================================================== PF operator: -108*t^2*D^3 - 324*t^2*D^2 - 312*t^2*D + D^3 - 96*t^2 Connection matrix: [ 0 24 0 576] [ 1 0 60 0] [ 0 1 0 24] [ 0 0 1 0] This is the cubic 3-fold
. This occurs for the following polytopes (PALP id, grdb id): [(231, 518837), (741, 547501)] The corresponding toric Fanos (for each polytope) have degrees: [24, 24] Each toric Fano has Hilbert series: 1 + 15*x + 65*x^2 + 175*x^3 + 369*x^4 + 671*x^5 + 1105*x^6 + 1695*x^7 + 2465*x^8 + 3439*x^9 + 4641*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 12, 0, 540, 0, 33600, 0, 2425500, 0, 190702512, 0, 15849497664, 0, 1369618398720, 0, 121821136479900, 0, 11079206239530000, 0] ================================================== PF operator: -3584*t^4*D^3 - 21504*t^4*D^2 - 2112*t^3*D^3 - 39424*t^4*D - 9504*t^3*D^2 - 368*t^2*D^3 - 21504*t^4 - 13728*t^3*D - 1104*t^2*D^2 - 12*t*D^3 - 6336*t^3 - 1088*t^2*D - 18*t*D^2 + D^3 - 352*t^2 - 6*t*D Connection matrix: [ 0 88 1584 11328] [ 1 6 228 1584] [ 0 1 6 88] [ 0 0 1 0] This occurs as a piece (the block 1, K, K^2, K^3) in the quantum cohomology of a hypersurface of bidegree (2,2) in
; as before this can be calculated using quantum Lefschetz. In particular, this is a G-Fano with
and the obvious G-action. This occurs for the following polytopes (PALP id, grdb id): [(2710, 530438), (2816, 355616), (3078, 466014), (3318, 545139), (3330, 526891), (3348, 525745), (3389, 321877), (3415, 317924), (3446, 147470), (3504, 610803), (3572, 452175), (3619, 306960), (3755, 446982), (3759, 446933), (3789, 294043), (3790, 294031), (3843, 585895), (3844, 585890), (3845, 585897), (3856, 585686), (3867, 29624), (3873, 5953), (3874, 5954), (3900, 442762), (3922, 283523), (3932, 281846), (3982, 573895), (4002, 522683), (4003, 522703), (4040, 275527), (4042, 274128), (4057, 87167), (4074, 566716), (4075, 566695), (4116, 269333), (4158, 435216), (4159, 434956), (4168, 264855), (4169, 263867), (4181, 72684), (4182, 72202), (4214, 261714), (4235, 544536), (4240, 520890), (4245, 432661), (4248, 432464), (4259, 431910), (4277, 431397), (4299, 520330)] The corresponding toric Fanos (for each polytope) have degrees: [12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12] Each toric Fano has Hilbert series: 1 + 9*x + 35*x^2 + 91*x^3 + 189*x^4 + 341*x^5 + 559*x^6 + 855*x^7 + 1241*x^8 + 1729*x^9 + 2331*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 44, 528, 11292, 228000, 4999040, 112654080, 2613620380, 61885803840, 1490373453744, 36386869189440, 898607084375616, 22407788170639872, 563420642442797568, 14268868232534243328, 363645785196486035100, 9319184268623160277632, 240004469570133005573264, 6208361451073231685966016] ================================================== PF operator: -256*t^4*D^3 - 1536*t^4*D^2 - 2816*t^4*D - 1536*t^4 + D^3 Connection matrix: [ 0 0 0 256] [ 1 0 0 0] [ 0 1 0 0] [ 0 0 1 0] This is
. This occurs for the following polytopes (PALP id, grdb id): [(0, 547386)] The corresponding toric Fanos (for each polytope) have degrees: [64] Each toric Fano has Hilbert series: 1 + 35*x + 165*x^2 + 455*x^3 + 969*x^4 + 1771*x^5 + 2925*x^6 + 4495*x^7 + 6545*x^8 + 9139*x^9 + 12341*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 0, 0, 24, 0, 0, 0, 2520, 0, 0, 0, 369600, 0, 0, 0, 63063000, 0, 0, 0] ================================================== PF operator: -192*t^3*D^3 - 864*t^3*D^2 - 80*t^2*D^3 - 1248*t^3*D - 240*t^2*D^2 - 4*t*D^3 - 576*t^3 - 256*t^2*D - 6*t*D^2 + D^3 - 96*t^2 - 2*t*D Connection matrix: [ 0 24 144 576] [ 1 2 36 144] [ 0 1 2 24] [ 0 0 1 0] This is a G-Fano. It occurs as the G-invariant piece (=span of 1, K, K^2, K^3) inside the quantum cohomology of the degree (1,1,1,1) hypersurface in
. The group G here is the symmetric group
acting in the obvious way (
would suffice). This occurs for the following polytopes (PALP id, grdb id): [(488, 543412), (577, 516786), (609, 425459), (1190, 507649), (1275, 413301), (1460, 250869), (1502, 674139), (1529, 12645), (1774, 408626), (1986, 534504), (1990, 534507), (2022, 491583), (2040, 491586), (2152, 387007), (2200, 222775), (2257, 234713), (2337, 61130), (2347, 60878), (2354, 1517), (2618, 204551), (2809, 468913), (2960, 195976), (3006, 646162), (3118, 463650), (3256, 160162), (3489, 135822), (3813, 290693)] The corresponding toric Fanos (for each polytope) have degrees: [24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24, 24] Each toric Fano has Hilbert series: 1 + 15*x + 65*x^2 + 175*x^3 + 369*x^4 + 671*x^5 + 1105*x^6 + 1695*x^7 + 2465*x^8 + 3439*x^9 + 4641*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 12, 48, 540, 4320, 42240, 403200, 4038300, 40958400, 423550512, 4434978240, 46982827584, 502437551616, 5417597053440, 58831951546368, 642874989479580, 7063600894137216, 77991775777488144, 864910651813116480] ================================================== PF operator: -336*t^4*D^3 - 2016*t^4*D^2 - 368*t^3*D^3 - 3696*t^4*D - 1656*t^3*D^2 - 112*t^2*D^3 - 2016*t^4 - 2392*t^3*D - 336*t^2*D^2 - 4*t*D^3 - 1104*t^3 - 336*t^2*D - 6*t*D^2 + D^3 - 112*t^2 - 2*t*D Connection matrix: [ 0 28 240 1120] [ 1 2 60 240] [ 0 1 2 28] [ 0 0 1 0] This is G-Fano
, see the comment below.
is a section of Segre variety
. This occurs for the following polytopes (PALP id, grdb id): [(1135, 539569), (1193, 507586), (1280, 413310), (1347, 413085), (1496, 674248), (1545, 537133), (1547, 537113), (1583, 500497), (1683, 402540), (1821, 236574), (1884, 672737), (1887, 672861), (2081, 388954), (2091, 388966), (2151, 388570), (2224, 222624), (2277, 662786), (2278, 662796), (2299, 662797), (2310, 668983), (2327, 61360), (2349, 12608), (2355, 10), (2411, 482428), (2480, 372136), (2539, 359406), (2548, 206001), (2579, 204760), (2643, 652681), (2653, 652715), (2665, 662262), (2681, 60032), (2688, 60031), (2697, 12519), (2721, 529907), (2742, 529800), (2748, 474431), (2761, 473110), (2780, 473340), (2819, 354967), (2820, 355397), (2889, 186748), (2915, 186256), (2954, 181697), (2974, 639652), (2975, 639467), (2995, 649245), (2999, 651604), (3009, 53121), (3028, 56368), (3076, 465966), (3089, 464399), (3133, 338175), (3134, 338158), (3200, 166803), (3253, 163000), (3270, 623294), (3302, 52267), (3336, 526335), (3354, 458626), (3401, 321330), (3420, 314336), (3439, 315731), (3477, 145166), (3494, 134327), (3500, 140258), (3524, 608931), (3539, 45839), (3551, 525020), (3590, 450075), (3603, 450158), (3633, 306075), (3668, 125301), (3704, 592333), (3774, 446837), (3805, 292773), (3860, 580376), (3892, 442983), (3979, 91442), (4014, 522631), (4016, 522644), (4027, 439692), (4176, 262193)] The corresponding toric Fanos (for each polytope) have degrees: [20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20] Each toric Fano has Hilbert series: 1 + 13*x + 55*x^2 + 147*x^3 + 309*x^4 + 561*x^5 + 923*x^6 + 1415*x^7 + 2057*x^8 + 2869*x^9 + 3871*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 14, 72, 882, 8400, 95180, 1060080, 12389650, 146472480, 1767391164, 21581516880, 266718438756, 3327025429728, 41849031952728, 530135326392672, 6757845419895570, 86619827323917888, 1115719258312182524, 14434274832755201424] ================================================== PF operator: -108*t^3*D^3 - 486*t^3*D^2 - 702*t^3*D - 324*t^3 + D^3 Connection matrix: [ 0 0 54 0] [ 1 0 0 54] [ 0 1 0 0] [ 0 0 1 0] This is the quadric 3-fold. This occurs for the following polytopes (PALP id, grdb id): [(1, 547378), (3, 544395)] The corresponding toric Fanos (for each polytope) have degrees: [54, 54] Each toric Fano has Hilbert series: 1 + 30*x + 140*x^2 + 385*x^3 + 819*x^4 + 1496*x^5 + 2470*x^6 + 3795*x^7 + 5525*x^8 + 7714*x^9 + 10416*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 0, 12, 0, 0, 540, 0, 0, 33600, 0, 0, 2425500, 0, 0, 190702512, 0, 0, 15849497664, 0] ================================================== PF operator: -16*t^4*D^3 - 96*t^4*D^2 - 176*t^4*D - 44*t^2*D^3 - 96*t^4 - 132*t^2*D^2 - 136*t^2*D + D^3 - 48*t^2 Connection matrix: [ 0 12 0 160] [ 1 0 20 0] [ 0 1 0 12] [ 0 0 1 0] This is
. This occurs for the following polytopes (PALP id, grdb id): [(42, 520063), (67, 430442), (220, 543857), (245, 518819)] The corresponding toric Fanos (for each polytope) have degrees: [40, 40, 40, 40] Each toric Fano has Hilbert series: 1 + 23*x + 105*x^2 + 287*x^3 + 609*x^4 + 1111*x^5 + 1833*x^6 + 2815*x^7 + 4097*x^8 + 5719*x^9 + 7721*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 6, 0, 114, 0, 2940, 0, 87570, 0, 2835756, 0, 96982116, 0, 3446781624, 0, 126047377170, 0, 4712189770860, 0] ================================================== PF operator: -3207168*t^4*D^3 - 19243008*t^4*D^2 - 387072*t^3*D^3 - 35278848*t^4*D - 1741824*t^3*D^2 - 14976*t^2*D^3 - 19243008*t^4 - 2515968*t^3*D - 44928*t^2*D^2 - 160*t*D^3 - 1161216*t^3 - 45504*t^2*D - 240*t*D^2 + D^3 - 15552*t^2 - 80*t*D Connection matrix: [ 0 3888 504576 18323712] [ 1 80 13600 504576] [ 0 1 80 3888] [ 0 0 1 0] This is the genus-3 Fano with b_2=1. This occurs for the following polytopes (PALP id, grdb id): [(4311, 547390)] The corresponding toric Fanos (for each polytope) have degrees: [4] Each toric Fano has Hilbert series: 1 + 5*x + 15*x^2 + 35*x^3 + 69*x^4 + 121*x^5 + 195*x^6 + 295*x^7 + 425*x^8 + 589*x^9 + 791*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 1944, 215808, 35295192, 5977566720, 1073491139520, 199954313717760, 38302652395770840, 7497487505353251840, 1493126207370030913344, 301572606517249894041600, 61627017349214878082106816, 12718722541880617724729659392, 2647214316675322606900471500288, 555025852555692350954771059458048, 117115566711982792889808392397460440, 24852125190258474673660570907685107712, 5300118106455156542190578158338402598464, 1135402757829368078738986314513572479911936] ================================================== PF operator: -216*t^4*D^3 - 1296*t^4*D^2 - 156*t^3*D^3 - 2376*t^4*D - 702*t^3*D^2 - 43*t^2*D^3 - 1296*t^4 - 1014*t^3*D - 129*t^2*D^2 - 2*t*D^3 - 468*t^3 - 134*t^2*D - 3*t*D^2 + D^3 - 48*t^2 - t*D Connection matrix: [ 0 12 90 360] [ 1 1 20 90] [ 0 1 1 12] [ 0 0 1 0] This is G-Fano: see example
in Galkin's paper here and a comment below. This occurs for the following polytopes (PALP id, grdb id): [(92, 544075), (128, 519656), (369, 254882), (420, 62083), (555, 516755), (635, 425353), (736, 674673), (738, 674678), (756, 546977), (776, 541681), (801, 541398), (830, 513201), (973, 420086), (976, 420478), (981, 419971), (1042, 253678), (1062, 253974), (1084, 674626), (1104, 674529), (1234, 506708), (1295, 413098), (1497, 673893), (1507, 674094), (1523, 61915), (1764, 400494), (1766, 400145), (1767, 400227), (1811, 236421), (1851, 236231), (1853, 236555), (1858, 245022), (1913, 672076), (1933, 61769), (2030, 490916), (2175, 385001), (2240, 221492), (2321, 667186), (2442, 481366), (2450, 479732), (2504, 370044), (2528, 372132), (2529, 371259), (2610, 202555), (2797, 472610), (2882, 346002), (3068, 527903), (3176, 331526), (3188, 332295), (3440, 314609), (3787, 446396)] The corresponding toric Fanos (for each polytope) have degrees: [30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30, 30] Each toric Fano has Hilbert series: 1 + 18*x + 80*x^2 + 217*x^3 + 459*x^4 + 836*x^5 + 1378*x^6 + 2115*x^7 + 3077*x^8 + 4294*x^9 + 5796*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 6, 24, 162, 1080, 7620, 55440, 415170, 3166800, 24570756, 193152960, 1535529996, 12323014704, 99702108792, 812367620064, 6660134536770, 54901225345824, 454766527525596, 3783396651070608] ================================================== PF operator: -304*t^4*D^3 - 1824*t^4*D^2 - 300*t^3*D^3 - 3344*t^4*D - 1350*t^3*D^2 - 88*t^2*D^3 - 1824*t^4 - 1950*t^3*D - 264*t^2*D^2 - 4*t*D^3 - 900*t^3 - 272*t^2*D - 6*t*D^2 + D^3 - 96*t^2 - 2*t*D Connection matrix: [ 0 24 198 880] [ 1 2 44 198] [ 0 1 2 24] [ 0 0 1 0] This is the genus-12 Fano with b_2=1. This occurs for the following polytopes (PALP id, grdb id): [(838, 513271), (929, 420909), (1021, 251679), (1027, 251680), (1140, 539490), (1271, 413299), (1312, 413150), (1427, 246241), (1481, 674247), (1483, 674241), (1603, 500036), (1699, 402281), (1715, 402297), (1721, 402434), (1785, 236692), (1815, 236477), (1854, 236595), (1879, 669463), (1885, 672886), (1886, 672906), (1888, 672877), (1897, 672700), (1898, 672887), (1900, 672881), (1928, 61779), (1929, 61780), (1936, 61803), (1941, 12639), (1942, 125), (2114, 388599), (2120, 387405), (2180, 223147), (2211, 222629), (2213, 222761), (2227, 222574), (2228, 222533), (2234, 222478), (2247, 222531), (2272, 662846), (2273, 662772), (2283, 662809), (2287, 662764), (2308, 668938), (2329, 61322), (2334, 61355), (2348, 12613), (2350, 12611), (2372, 531930), (2458, 372905), (2466, 372746), (2494, 370851), (2502, 370599), (2522, 370618), (2584, 202565), (2591, 202512), (2596, 204789), (2599, 203231), (2617, 204738), (2642, 652718), (2654, 662248), (2656, 660114), (2660, 662294), (2661, 662301), (2663, 662177), (2664, 660113), (2691, 60018), (2693, 59484), (2695, 59329), (2696, 12518), (2701, 12361), (2760, 472027), (2825, 354996), (2841, 353944), (2843, 353483), (2851, 352703), (2905, 186059), (2913, 186612), (2916, 186255), (2919, 186187), (2932, 181709), (2933, 181894), (2935, 181758), (2936, 181988), (2952, 181692), (2973, 639032), (2991, 638807), (2998, 651804), (3003, 651573), (3015, 56731), (3016, 57186), (3017, 57061), (3021, 57254), (3029, 56365), (3093, 464170), (3127, 337772), (3148, 337640), (3156, 333577), (3224, 165968), (3235, 163475), (3237, 161994), (3239, 160242), (3246, 163474), (3247, 161995), (3248, 161991), (3249, 163471), (3254, 160747), (3269, 622927), (3271, 624138), (3283, 624083), (3284, 624143), (3301, 51708), (3305, 50760), (3362, 456388), (3364, 456230), (3365, 456769), (3370, 456302), (3380, 456300), (3419, 315934), (3430, 315935), (3431, 314507), (3458, 144273), (3482, 140624), (3487, 136237), (3492, 140571), (3493, 140188), (3498, 140567), (3499, 140594), (3526, 619055), (3588, 451905), (3629, 305845), (3655, 300039), (3656, 301802), (3687, 125281), (3694, 116207), (3714, 592519), (3771, 446183), (3818, 291701), (3819, 287964), (3840, 100388), (3842, 100550), (3909, 442425), (3917, 442338), (3959, 277791), (4036, 438626), (4053, 271678), (4054, 272813), (4128, 266401), (4154, 521439)] The corresponding toric Fanos (for each polytope) have degrees: [22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22, 22] Each toric Fano has Hilbert series: 1 + 14*x + 60*x^2 + 161*x^3 + 339*x^4 + 616*x^5 + 1014*x^6 + 1555*x^7 + 2261*x^8 + 3154*x^9 + 4256*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 12, 60, 636, 5760, 58620, 604800, 6447420, 70022400, 773578512, 8660892240, 98071697724, 1121159239200, 12922708539312, 150012340798320, 1752282573404220, 20581063744475520, 242914688315991120, 2879646849072124560] ================================================== PF operator: -256*t^2*D^3 - 768*t^2*D^2 - 704*t^2*D + D^3 - 192*t^2 Connection matrix: [ 0 48 0 2304] [ 1 0 160 0] [ 0 1 0 48] [ 0 0 1 0] This is
. This occurs for the following polytopes (PALP id, grdb id): [(427, 547520)] The corresponding toric Fanos (for each polytope) have degrees: [16] Each toric Fano has Hilbert series: 1 + 11*x + 45*x^2 + 119*x^3 + 249*x^4 + 451*x^5 + 741*x^6 + 1135*x^7 + 1649*x^8 + 2299*x^9 + 3101*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 24, 0, 2520, 0, 369600, 0, 63063000, 0, 11732745024, 0, 2308743493056, 0, 472518347558400, 0, 99561092450391000, 0, 21452752266265320000, 0] ================================================== PF operator: -1840*t^4*D^3 - 11040*t^4*D^2 - 1208*t^3*D^3 - 20240*t^4*D - 5436*t^3*D^2 - 243*t^2*D^3 - 11040*t^4 - 7852*t^3*D - 729*t^2*D^2 - 10*t*D^3 - 3624*t^3 - 742*t^2*D - 15*t*D^2 + D^3 - 256*t^2 - 5*t*D Connection matrix: [ 0 64 924 5936] [ 1 5 140 924] [ 0 1 5 64] [ 0 0 1 0] This is the genus-8 Fano with b_2=1. This occurs for the following polytopes (PALP id, grdb id): [(2365, 532085), (2400, 483089), (2463, 372785), (2471, 372935), (2552, 206003), (2752, 474446), (2764, 473336), (2823, 355511), (2965, 639875), (3055, 527980), (3081, 465958), (3129, 338179), (3201, 166804), (3213, 165796), (3215, 166501), (3218, 166517), (3228, 166494), (3265, 625365), (3267, 625031), (3282, 625034), (3297, 47449), (3334, 526350), (3350, 458642), (3396, 321233), (3398, 321301), (3399, 321302), (3447, 147436), (3460, 146429), (3470, 146472), (3505, 610621), (3508, 610744), (3510, 610784), (3529, 41168), (3534, 41131), (3535, 41126), (3536, 41127), (3542, 9094), (3543, 9098), (3558, 524993), (3573, 452201), (3586, 449943), (3623, 306022), (3628, 305762), (3632, 306089), (3635, 306132), (3636, 306131), (3639, 299475), (3665, 129152), (3669, 125267), (3674, 127678), (3675, 127722), (3697, 597527), (3700, 597556), (3703, 597738), (3711, 596349), (3717, 34551), (3718, 34356), (3723, 7560), (3764, 445117), (3765, 445154), (3793, 292448), (3798, 292446), (3799, 292443), (3823, 112305), (3824, 112517), (3831, 108038), (3836, 110185), (3846, 585232), (3848, 585544), (3851, 585519), (3854, 585566), (3855, 584997), (3866, 29610), (3869, 28871), (3870, 28930), (3875, 5946), (3886, 523387), (3890, 442981), (3895, 442754), (3899, 442953), (3924, 283515), (3928, 282712), (3930, 282243), (3931, 281904), (3934, 282251), (3943, 282871), (3946, 283322), (3962, 98196), (3967, 93948), (3969, 94721), (3972, 93843), (3975, 94624), (3976, 95280), (3981, 574884), (3985, 574262), (3991, 24223), (4008, 522622), (4033, 438004), (4045, 274849), (4048, 273916), (4056, 86778), (4060, 87169), (4061, 82704), (4065, 85225), (4068, 86228), (4076, 564955), (4077, 565284), (4078, 565273), (4097, 521909), (4110, 435745), (4119, 269275), (4125, 268804), (4126, 269009), (4135, 77741), (4137, 76994), (4138, 77044), (4139, 75065), (4165, 434943), (4170, 264166), (4172, 264772), (4184, 69823), (4191, 521209), (4197, 521161), (4200, 433641), (4206, 433730), (4208, 433608), (4220, 261600), (4222, 261134), (4223, 261536), (4225, 67721), (4239, 520906), (4252, 259188), (4261, 431894), (4270, 257604)] The corresponding toric Fanos (for each polytope) have degrees: [14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14, 14] Each toric Fano has Hilbert series: 1 + 10*x + 40*x^2 + 105*x^3 + 219*x^4 + 396*x^5 + 650*x^6 + 995*x^7 + 1445*x^8 + 2014*x^9 + 2716*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 32, 312, 5520, 91680, 1651640, 30604560, 583436560, 11352768000, 224645958432, 4506386808000, 91434963225144, 1873214113234464, 38695098186167280, 805079741247573792, 16855708323075233040, 354862100179318727424, 7507744262279847981824, 159540694369215435619200] ================================================== PF operator: -165888*t^4*D^3 - 995328*t^4*D^2 - 39744*t^3*D^3 - 1824768*t^4*D - 178848*t^3*D^2 - 3024*t^2*D^3 - 995328*t^4 - 258336*t^3*D - 9072*t^2*D^2 - 60*t*D^3 - 119232*t^3 - 9216*t^2*D - 90*t*D^2 + D^3 - 3168*t^2 - 30*t*D Connection matrix: [ 0 792 43632 793152] [ 1 30 2340 43632] [ 0 1 30 792] [ 0 0 1 0] This is the genus-4 Fano with b_2=1. This occurs for the following polytopes (PALP id, grdb id): [(4281, 547396), (4283, 544447), (4285, 520428), (4286, 520416), (4296, 520331), (4309, 520190), (4317, 547387)] The corresponding toric Fanos (for each polytope) have degrees: [6, 6, 6, 6, 6, 6, 6] Each toric Fano has Hilbert series: 1 + 6*x + 20*x^2 + 49*x^3 + 99*x^4 + 176*x^5 + 286*x^6 + 435*x^7 + 629*x^8 + 874*x^9 + 1176*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 396, 17616, 1217052, 85220640, 6349812480, 490029523200, 38883641777820, 3152020367254080, 259917911904104496, 21734333812757966400, 1838661488140000620096, 157079889830458865926656, 13532851175260662410660352, 1174404851170539753963534336, 102567197002978827892527466140, 9008119389478435783966748566656, 795101313792044241851836759258896, 70492745075535384957296839185342912] ================================================== PF operator: -1024*t^4*D^3 - 6144*t^4*D^2 - 768*t^3*D^3 - 11264*t^4*D - 3456*t^3*D^2 - 176*t^2*D^3 - 6144*t^4 - 4992*t^3*D - 528*t^2*D^2 - 8*t*D^3 - 2304*t^3 - 544*t^2*D - 12*t*D^2 + D^3 - 192*t^2 - 4*t*D Connection matrix: [ 0 48 576 3328] [ 1 4 96 576] [ 0 1 4 48] [ 0 0 1 0] This is the genus-9 Fano with b_2=1. This occurs for the following polytopes (PALP id, grdb id): [(1953, 546004), (2009, 492045), (2023, 491381), (2092, 388964), (2196, 223136), (2290, 662829), (2413, 482431), (2436, 482420), (2481, 372120), (2497, 372105), (2649, 652773), (2723, 529956), (2772, 473102), (2887, 186783), (2890, 186772), (2893, 186627), (2895, 186614), (2896, 186640), (2898, 186626), (2902, 186306), (2966, 639881), (2968, 639889), (2986, 639750), (2987, 639688), (2989, 639751), (3007, 53123), (3011, 53112), (3012, 53111), (3025, 57234), (3026, 57359), (3031, 11582), (3033, 12197), (3111, 464458), (3128, 338106), (3130, 338225), (3131, 338235), (3161, 335117), (3208, 166302), (3209, 165850), (3226, 166025), (3276, 624084), (3279, 624186), (3293, 47436), (3295, 47424), (3299, 52868), (3308, 11546), (3309, 11569), (3311, 1454), (3338, 526791), (3356, 458619), (3372, 455988), (3373, 456763), (3374, 456807), (3375, 456805), (3395, 321327), (3400, 321353), (3408, 321054), (3454, 145662), (3461, 145189), (3463, 146791), (3472, 146294), (3476, 146798), (3511, 610605), (3512, 610156), (3514, 608808), (3517, 608909), (3518, 608870), (3528, 41156), (3530, 40830), (3531, 40767), (3532, 41052), (3537, 41139), (3541, 9091), (3545, 10501), (3600, 450189), (3601, 449940), (3613, 449941), (3641, 299999), (3647, 301745), (3663, 129141), (3673, 126173), (3684, 126035), (3685, 125153), (3686, 125313), (3699, 597548), (3702, 597551), (3708, 595052), (3709, 595268), (3710, 595226), (3719, 34364), (3720, 40408), (3724, 1223), (3741, 524265), (3758, 446950), (3782, 445152), (3796, 293345), (3797, 292762), (3801, 292681), (3802, 292451), (3815, 288486), (3827, 112423), (3829, 108209), (3832, 109121), (3835, 111932), (3850, 585038), (3853, 584967), (3857, 579004), (3859, 580257), (3863, 582522), (3864, 582645), (3871, 28869), (3872, 28187), (3903, 443014), (3913, 442583), (3933, 283208), (3938, 281831), (3944, 282143), (3953, 278160), (3971, 94626), (3974, 93844), (3988, 569725), (3989, 568994), (3992, 23122), (3997, 544752), (4015, 522325), (4044, 275383), (4049, 272798), (4062, 82771), (4064, 85219), (4066, 85150), (4071, 86196), (4108, 436835), (4120, 268442), (4136, 76930), (4145, 555757), (4149, 521466), (4151, 521506), (4162, 435181), (4163, 434689), (4164, 434819), (4171, 264649), (4174, 264553), (4226, 67006), (4263, 431653), (4301, 520292)] The corresponding toric Fanos (for each polytope) have degrees: [16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16] Each toric Fano has Hilbert series: 1 + 11*x + 45*x^2 + 119*x^3 + 249*x^4 + 451*x^5 + 741*x^6 + 1135*x^7 + 1649*x^8 + 2299*x^9 + 3101*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 24, 192, 2904, 40320, 611520, 9515520, 152412120, 2491104000, 41404233024, 697598415360, 11887922751936, 204543454123008, 3548536418059776, 62004013026988032, 1090207952792089560, 19275174299698656768, 342468223449089584704, 6111542317740696764928] ================================================== PF operator: 144*t^4*D^3 + 864*t^4*D^2 + 1584*t^4*D - 40*t^2*D^3 + 864*t^4 - 120*t^2*D^2 - 128*t^2*D + D^3 - 48*t^2 Connection matrix: [ 0 12 0 0] [ 1 0 16 0] [ 0 1 0 12] [ 0 0 1 0] This is
. This occurs for the following polytopes (PALP id, grdb id): [(17, 544342), (30, 520140), (121, 519664), (155, 430096)] The corresponding toric Fanos (for each polytope) have degrees: [48, 48, 48, 48] Each toric Fano has Hilbert series: 1 + 27*x + 125*x^2 + 343*x^3 + 729*x^4 + 1331*x^5 + 2197*x^6 + 3375*x^7 + 4913*x^8 + 6859*x^9 + 9261*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 6, 0, 90, 0, 1860, 0, 44730, 0, 1172556, 0, 32496156, 0, 936369720, 0, 27770358330, 0, 842090474940, 0] ================================================== PF operator: -2160*t^4*D^3 - 12960*t^4*D^2 - 1728*t^3*D^3 - 23760*t^4*D - 7776*t^3*D^2 - 360*t^2*D^3 - 12960*t^4 - 11232*t^3*D - 1080*t^2*D^2 - 16*t*D^3 - 5184*t^3 - 1152*t^2*D - 24*t*D^2 + D^3 - 432*t^2 - 8*t*D Connection matrix: [ 0 108 1728 13824] [ 1 8 208 1728] [ 0 1 8 108] [ 0 0 1 0] ??? currently unknown: conjecturally a G-Fano, arising as a piece of the quantum cohomology of a 2:1 cover of
branched over a (2,2,2) hypersurface. This occurs for the following polytopes (PALP id, grdb id): [(2816, 355616), (3328, 545072), (3349, 525553), (3392, 321879), (3446, 147470), (3504, 610803), (3739, 524375), (3790, 294031), (3794, 292940), (3843, 585895), (3844, 585890), (3845, 585897), (3867, 29624), (3873, 5953), (3874, 5954), (3966, 95245), (4026, 439663), (4057, 87167), (4074, 566716), (4075, 566695), (4168, 264855), (4181, 72684), (4182, 72202), (4240, 520890), (4248, 432464)] The corresponding toric Fanos (for each polytope) have degrees: [12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12] Each toric Fano has Hilbert series: 1 + 9*x + 35*x^2 + 91*x^3 + 189*x^4 + 341*x^5 + 559*x^6 + 855*x^7 + 1241*x^8 + 1729*x^9 + 2331*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 54, 672, 15642, 336960, 7919460, 191177280, 4751272890, 120527514240, 3109617573804, 81336932550720, 2152021034457756, 57492903382282368, 1548779408915134968, 42023349488330001792, 1147430010272379786810, 31504595489224640310528, 869291145239891056320924, 24092072648449534765168704] ================================================== PF operator: -64*t^2*D^3 - 192*t^2*D^2 - 192*t^2*D + D^3 - 64*t^2 Connection matrix: [ 0 16 0 256] [ 1 0 32 0] [ 0 1 0 16] [ 0 0 1 0] This is
. This occurs for the following polytopes (PALP id, grdb id): [(8, 547367), (91, 544065), (119, 519672), (153, 430103), (197, 255744), (428, 547516), (432, 547285), (433, 547298)] The corresponding toric Fanos (for each polytope) have degrees: [32, 32, 32, 32, 32, 32, 32, 32] Each toric Fano has Hilbert series: 1 + 19*x + 85*x^2 + 231*x^3 + 489*x^4 + 891*x^5 + 1469*x^6 + 2255*x^7 + 3281*x^8 + 4579*x^9 + 6181*x^10 + O(x^11) The first 20 coefficients of the period are: [1, 0, 8, 0, 216, 0, 8000, 0, 343000, 0, 16003008, 0, 788889024, 0, 40424237568, 0, 2131746903000, 0, 114933031928000, 0] ==================================================
This can be done by quantum Lefschetz since this variety is a hypersurface in smooth toric Fano fourfold
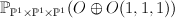
Some other notes.
Denote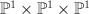 by UU,
by UU,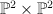 by W,
by W,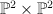 by V.
by V.
double cover of UU branched in divisor of degree (2,,2,2) by U,
divisor of bidegree (1,1) in
divisor of bidegree (2,2) in
QDE for U is derived from UU in the same way as V is derived from W:
first replace t^2 with t, then shift Givental’s costant to zero.
Hyperplane section of W and UU conicide – it is a del Pezzo surface of degree 6, so their irreducible parts of QDE’s are also related by a “house”.
On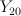 .
.
It has a terminal representative
[1 0 0 -1 2 1 1 -1 -1 -2 1 0 0 -1]
[0 1 0 1 -1 0 -1 1 0 1 -1 0 -1 0]
[0 0 1 1 -1 -1 0 0 1 1 -1 -1 0 0]
so it is a degeneration of smooth Fano variety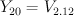
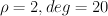 and
and 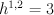 .
.
with
There are exactly 8 families containing G-Fano threefolds. 7 were already listed. The last one is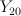 – it is a blowup of
– it is a blowup of 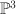 with the center in the curve of genus 3 and degree 6 (which is intersection of cubics).
with the center in the curve of genus 3 and degree 6 (which is intersection of cubics).
It is an intersection of three divisors of bi-degree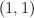 on
on 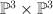 , so also can be done by quantum Lefschetz.
, so also can be done by quantum Lefschetz.
after normalizing (shift of Givental’s constant to 0) it becomes
On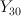 .
.
It is intersection of divisors of polydegrees .
.
(1,1,0),(1,0,1) and (0,1,1) on
Up to Givental’s constant it’s $I$-series are
after the shift of Givental’s constant to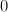 it becomes
it becomes
On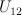 :
:
Cone F over Segre variety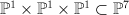
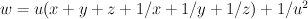
has index 3, and its mirror is isogeneous to
So its regularized I-series are
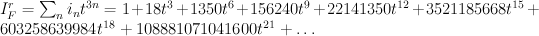
Then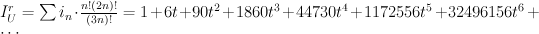
Normalizing gives period sequence: