Fano Varieties and Extremal Laurent Polynomials

del Pezzo surfaces

Here are the G-functions (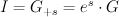 $I = G_{+s} = e^s \cdot G$ )
and regularized quantum periods (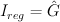 $I_{reg} = \hat{G}$ )
for del Pezzo surfaces.

The del Pezzo surface of degree 9

This is the toric variety $\PP^2$ . We have:
$G(t) = \sum_k {t^{3k} \over k!k!k!} = 1+t^3+\frac{t^6}{8}+\frac{t^9}{216}+\cdots$
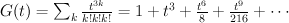
and the regularized quantum period is:
$\hat{G}(t) = 1+6 t^3+90 t^6+1680 t^9+\cdots$

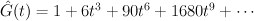
The del Pezzo surface of degree 8, case a

This is the toric variety 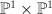$\PP^1 \times \PP^1$ . We have:
$G(t) = \sum_{k,l} {t^{2k+2l} \over k!k!l!l!} = 1+2 t^2+\frac{3 t^4}{2}+\frac{5 t^6}{9}+\cdots$
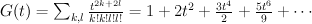
and the regularized quantum period is:
$\hat{G}(t) = 1+4 t^2+36 t^4+400 t^6+\cdots$

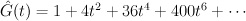
The del Pezzo surface of degree 8, case b

This is the toric variety 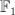$\mathbb{F}_1$ . We have:
$G(t) = \sum_{k,l} {t^{2k+l} \over k!l!l!(k-l)!} = 1+t^2+t^3+\frac{t^4}{4}+\frac{t^5}{2}+\frac{11 t^6}{72}+\frac{t^7}{12}+\cdots$
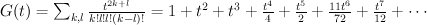
and the regularized quantum period is:
$\hat{G}(t) = 1+2 t^2+6 t^3+6 t^4+60 t^5+110 t^6+420 t^7+\cdots$

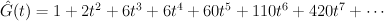
The del Pezzo surface of degree 7

This is the blow-up of $\PP^2$ in two points. It is a toric variety. We have:
$G(t) = \sum_{k,l,m} {t^{2k+3l+2m} \over (l+m)!(k+l)!m!l!k!} =1+2 t^2+t^3+\frac{3 t^4}{2}+t^5+\frac{49 t^6}{72}+\frac{5 t^7}{12}+\cdots$
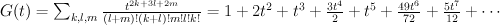
and the regularized quantum period is:
$\hat{G}(t) = 1+4 t^2+6 t^3+36 t^4+120 t^5+490 t^6+2100 t^7+\cdots$

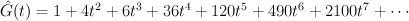
The del Pezzo surface of degree 6

This is the blow-up of $\PP^2$ in three points. It is a toric variety. We have:
$G(t) = \sum_{k,l,m,n} {t^{k+2l+2m+n} \over (-k+m+n)!(k+l-n)!n!m!l!k!} =1+3 t^2+2 t^3+\frac{15 t^4}{4}+3 t^5+\frac{17 t^6}{6}+2 t^7+\cdots$
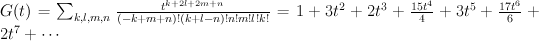
and the regularized quantum period is:
$\hat{G}(t) = 1+6 t^2+12 t^3+90 t^4+360 t^5+2040 t^6+10080 t^7+\cdots$

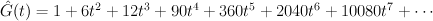
The del Pezzo surface of degree 5

This is a hypersurface of bidegree 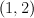$(1,2)$ in $\PP^1 \times \PP^2$ . We have:
$G_{+3}(t) = \sum_{k,l} t^{k+l} {(k+2l)! \over k!k!l!l!l!} = 1+3 t+\frac{19 t^2}{2}+\frac{49 t^3}{2}+\frac{417 t^4}{8}+\frac{3751 t^5}{40}+\frac{104959 t^6}{720}+\frac{334769 t^7}{1680}+\cdots$
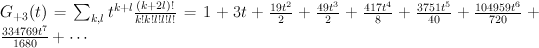
and the regularized quantum period is:
$\hat{G}(t) = 1+10 t^2+30 t^3+270 t^4+1560 t^5+11350 t^6+77700 t^7+\cdots$

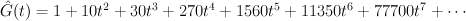
The del Pezzo surface of degree 4

This is a (2,2) complete intersection in 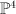$\PP^4$ . We have:
$G_{+4}(t) = \sum_k t^{k} {(2k)!(2k)! \over k!k!k!k!k!} = 1+4 t+18 t^2+\frac{200 t^3}{3}+\frac{1225 t^4}{6}+\frac{2646 t^5}{5}+\frac{5929 t^6}{5}+\frac{81796 t^7}{35}+\cdots$
and the regularized quantum period is:
$\hat{G}(t) = 1+20 t^2+96 t^3+1188 t^4+10560 t^5+111440 t^6+1142400 t^7+\cdots$

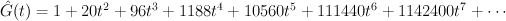
The del Pezzo surface of degree 3

This is the cubic surface in $\PP^3$ . We have:
$G_{+6}(t) = \sum_k t^{k} {(3k)!\over k!k!k!k!} = 1+6 t+45 t^2+280 t^3+\frac{5775 t^4}{4}+\frac{63063 t^5}{10}+\frac{119119 t^6}{5}+\frac{554268 t^7}{7}+\cdots$
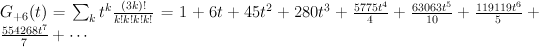
and the regularized quantum period is:
$\hat{G}(t) = 1+54 t^2+492 t^3+9882 t^4+158760 t^5+2879640 t^6+51982560 t^7+\cdots$

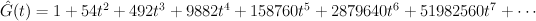
The del Pezzo surface of degree 2

This is the quartic surface in 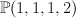$\PP(1,1,1,2)$ . We have:
$G_{+12}(t) = \sum_k t^{k} {(4k)!\over k!k!k!(2k)!} = 1+12 t+210 t^2+3080 t^3+\frac{75075 t^4}{2}+\frac{1939938 t^5}{5}+\frac{52055003 t^6}{15}+\frac{191222460 t^7}{7}+\cdots$
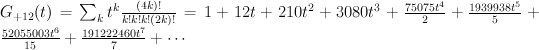
and the regularized quantum period is:
$\hat{G}(t) = 1+276 t^2+6816 t^3+314532 t^4+12853440 t^5+569409360 t^6+25533244800 t^7 +\cdots$

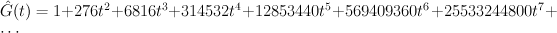
The del Pezzo surface of degree 1

This is the sextic surface in 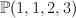$\PP(1,1,2,3)$ . We have:
$G_{+60}(t) = \sum_k t^{k} {(6k)!\over k!k!(2k)!(3k)!} = 1+60 t+6930 t^2+680680 t^3+\frac{111546435 t^4}{2}+3881815938 t^5+233987238485 t^6+\frac{86928646722060 t^7}{7}+\cdots$
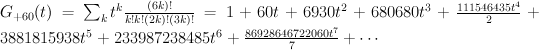
and the regularized quantum period is:
$\hat{G}(t) = 1 + 10260 t^2 + 2021280 t^3 + 618874020 t^4 + 184450426560 t^5 + 57876331467600 t^6 + 18570232920355200 t^7+\cdots$

Comment (RSS) | Trackback

2 Comments

Tom says:

February 27, 2012 at 12:54 pm

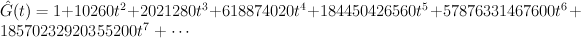
See the previous incarnation of this page:

http://coates.ma.ic.ac.uk/fanosearch/?p=5093

for some informative comments.
Sergey says:

March 9, 2012 at 4:34 pm

The (anticanonical) spectra of del Pezzo surfaces.

$c_9 = 1-27 t^3$ (T=3)
$c_q = t^2 (1-16 t^2)$ (T=4)
$c_8 = 1 + t - 8 t^2 - 36 t^3 - 11 t^4$ (T~3.79)
$c_7 = (1+t) (1 + t - 18 t^2 - 43 t^3)$ (T~4.72)
$c_6 = (1+3 t) (1+2 t) (1-6 t)$ (T=6)
$c_5 = (1+3 t) (1-5 t-25 t^2)$ (T~8.09)
$c_4 = (1+4 t) (1-12 t)$ (T=12)
$c_3 = (1+6 t) (1-21 t)$ (T=21)
$c_2 = (1+12 t) (1-52 t)$ (T=52)
$c_1 = (1+60 t) (1-372 t)$ (T=372)

Copy-paste edition:

c9 = 1-27*t^3;
cq = t^2*(1-16*t^2);
c8 = 1 + t – 8*t^2 – 36*t^3 – 11*t^4;
c7 = (1+t) * (1 + t – 18*t^2 – 43*t^3);
c6 = (1+3*t)*(1+2*t)*(1-6*t);
c5 = (1+3*t)*(1-5*t-25*t^2);
c4 = (1+4*t)(1-12*t);
c3 = (1+6*t)*(1-21*t);
c2 = (1+12*t)*(1-52*t);
c1 = (1+60*t)*(1-372*t);