December 11, 2012, 2:44 pm
We just posted two papers to the arXiv:
arXiv:1212.1722 Mirror symmetry and Fano manifolds (Coates, Corti, Galkin, Golyshev, Kasprzyk). This announces our program.
arXiv:1212.1785 Minkowski polynomials and mutations (Akhtar, Coates, Galkin, Kasprzyk). This gives a very clean and satisfactory explanation of why a 3-dimensional Fano manifold will in general have many different Minkowski polynomials as mirrors.
The ordering of the 165 period sequences in the second paper is not the same the one in this blog’s page “3d Minkowski period sequences”
In the new scheme period sequences are ordered lexicographically http://grdb.lboro.ac.uk/forms/period3
Update: the correspondence between smooth Fano 3-folds and period sequences (with the new ids) is here. We will sort out the rest of the blog shortly.
May 12, 2012, 7:56 pm
Welcome to the new readers whom we met at the Imperial Festival. A quick guide to the site:
- a good introduction to the project is here; there are also images and animations.
- there are several posts describing our work in progress with artist Gemma Anderson.
- for more mathematical details, scroll down or look at the data linked from the tabs above (called “Fano Varieties”, “3D Minkowski Period Sequences”, and “3D Reflexive Polytopes”)
Popular science articles describing the project appeared in Cosmos, New Scientist, and Physics World.
February 25, 2012, 1:03 pm
The updated script for computing Picard lattices of Fano threefolds: now it works and, even better, computes all five principal invariants of the smoothing!
Picard lattices of ambiguous nodal toric Fano threefolds
Let  be a nodal toric Fano threefold (recall that in toric world terminal Gorenstein singularities of Fano threefolds are simply ordinary double points aka nodes
be a nodal toric Fano threefold (recall that in toric world terminal Gorenstein singularities of Fano threefolds are simply ordinary double points aka nodes ![(xy=zt) \subset \CC^4 = \mathrm{Spec } \CC[x,y,z,t] (xy=zt) \subset \CC^4 = \mathrm{Spec } \CC[x,y,z,t]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/232/2322caf126e6be2e67d7eb088fd671e9-ffffff-000000-0.png) ).
).
Given a terminal Gorenstein toric Fano threefold  ,
,
this script do the following:
1. Compute Picard lattice 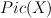
2. Then compute (self)intersection theory on this lattice.
This part is done in 3 steps:
a. pick a small crepant resolution 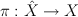
b. compute intersection theory of smooth toric manifold 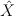 ,
,
c. restrict intersection theory from 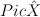 to
to 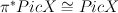 .
.
3. Threefold X has a unique deformation class of smoothing by Fano threefold Y
We also compute the principal invariants of Y: Betti numbers, degree, Lefschetz discriminant and Fano index
The main procedure is called Picard(toric)
The input is a 3-component vector toric=[description, vertices, faces]
description is a verbal description of variety X (not used for computations)
vertices is a matrix of vertices of the fan polytope Delta(X)
faces is a transposed matrix of faces (vertices of the moment polytope)
The output is a 2-component vector o = [lattice, invariants]
where lattice is 3-component vector [cubic, M, class]
cubic is homogenous cubic polynomial of ‘rk Pic(X)’ variables (self-intersection pairing)
class is the expression of the first Chern class in terms of generators of Picard group
M is the matrix of the Lefschetz pairing ![(a,b) \to \int_{[X]} a \cup b \cup c_1(X) (a,b) \to \int_{[X]} a \cup b \cup c_1(X)](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/bc1/bc107c1ee4b059ffa052e7bdad6cce49-ffffff-000000-0.png)
and invariants is 5-component vector [rho,deg,b,d,r] of the principal invariants
rho is Picard number i.e. second Betti number of X
deg is the anticanonical degree ![\int_{[X]} c_1(X)^3 \int_{[X]} c_1(X)^3](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/ccc/cccf259f6d55f73d0b09adfa44414f00-ffffff-000000-0.png)
b is the half of third Betti number of the smoothing Y
d is the Lefschetz discriminant (i.e. determinant of matrix M)
r is the Fano index (i.e. divisibility of  in
in 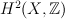 )
)
February 24, 2012, 4:10 pm
Just noticed I forgot to upload the updated (but still incomplete) Split notes:
Split notes -1,2,3
February 14, 2012, 10:54 pm
Three years ago I lost the tex-file of Small toric degenerations of Fano threefolds and unfortunately haven’t found since then. But instead I typed it again! Voila! (so far only a “twitter version” – just a statement of the theorem and the table, no unnecessary proofs or applications).
February 14, 2012, 10:23 pm
I was reading an amusing paper of Ronald van Luijk: he demonstrates
the K3 surface with Picard number one.
Reflecting his proof I formulate the following unexpected principle:
in order to classify Fanos with Picard number 1
we should NOT just get rid of all polytopes with higher Picard number !
One of the reasons is as follows:
0. Assume we’ve done with computing basic invariants of polytopes,
including Picard numbers
1. Assume we’ve done with the initial step of creating some database
of prospective Laurent polynomials out of many many polytopes
2. It is much easier to create a “phone book” of period sequences (say
first 10 or 20 coefficients) then to compute their Picard–Fuchs
operators.
3. Once we have a “phone book” prospective polynomials W fall into
equivalence classes with respect to initial terms of their period
sequences
If we manage how to program Cremona-equivalence then they fall
into even better classes.
4. Now, under assumption that Laurent polynomial W reflects a toric
degeneration of Fano manifold X into the toric variety X_0 that W is
supported on (i.e. Newton(W) is dual to Moment(X_0))
$ rk Pic X \geq \rk \Pic X_0 $
5. So if we know that period sequence is supported on some toric
variety with Picard number > 1 – then it is not a period sequence of
Fano with Picard number 1
If we would drop polytopes with Picard number >1, then we have to
do extra work!
In fact we used this ideas for threefolds before we computed their
G-series by ad hoc and a posteriori methods.
By a posteriori I mean it is not so easy to tell what is Picard number
of Fano variety from its G-series and/or differential operator that
annihilates it:
G-series for Fano varieties with Picard number 1 and for G-minimal
(hence quantum minimal) varieties look pretty much the same.
February 7, 2012, 6:45 pm
In December 2011, at the Royal Society (London) Tom, Al and I discussed the possibilities of creating Sliceforms of Calabi-Yau forms. Sliceforms are geometric models constructed from interlocking sets of planar pieces. The basic idea behind sliceform construction is indicated in the photos. By creating two sets of slotted pieces (“slot-from-the-top” and “slot-from-the-bottom” sets) that intersect at right angles, one can link the two sets together to form models of surfaces and solids.
The Sliceform technique originated with a mathematician called Olaus Henrici who taught in London at the end of the nineteenth and early twentieth centuries. He made models using cross sections of quartic surfaces; these are similar to a sphere but have with cross sections which are ellipses, hyperbolae or parabolae.
Models were constructed for sale in Germany by the firm of Martin Schilling. These were designed by Alexander von Brill in Darmstadt. In the nineteenth century mathematical models (paper/wood/ceramic) were made for teaching and understanding geometry. They where also inspirational to artists such as Barbara Hepworth and Naum Gabo.
The Science Museum (London) exhibits a collection of Sliceforms from the 19th century to the present day (by Brill and John Sharp) they have an austere and utilitarian beauty, and where the original inspiration for developing sliceforms of the Calabi-Yau forms with Tom and Al.
Once I had cut the pieces of the sliceform out Tom cleverly pieced it together and you can see Tom and Alessios’ delight in the model…
August 2, 2011, 3:36 pm
First part of my talk in Split – importance of real positivity (phase=0) and convexity.
split1
July 25, 2011, 11:14 am
We are collaborating with artist and printmaker Gemma Anderson to produce artworks based on the Fanosearch project. Here is some of her work in progress:
July 19, 2011, 8:15 pm
This is a workaround for this very unfortunate bug in Sage, based on Sage 4.7. The patch is a horrible kludge (it just turns multi-modular matrix multiplication off completely) but will at least fix the problem until I get time to work up a proper patch. Save the file, remove the ‘.txt’ extension, clone a new copy of Sage, and then apply the patch using:
hg_sage.apply("<full-path-and-filename.patch>")
from the Sage command line.
 be a nodal toric Fano threefold (recall that in toric world terminal Gorenstein singularities of Fano threefolds are simply ordinary double points aka nodes
be a nodal toric Fano threefold (recall that in toric world terminal Gorenstein singularities of Fano threefolds are simply ordinary double points aka nodes ![(xy=zt) \subset \CC^4 = \mathrm{Spec } \CC[x,y,z,t] (xy=zt) \subset \CC^4 = \mathrm{Spec } \CC[x,y,z,t]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/232/2322caf126e6be2e67d7eb088fd671e9-ffffff-000000-0.png) ).
).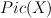
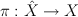
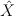 ,
,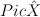 to
to 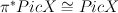 .
.![(a,b) \to \int_{[X]} a \cup b \cup c_1(X) (a,b) \to \int_{[X]} a \cup b \cup c_1(X)](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/bc1/bc107c1ee4b059ffa052e7bdad6cce49-ffffff-000000-0.png)
![\int_{[X]} c_1(X)^3 \int_{[X]} c_1(X)^3](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/ccc/cccf259f6d55f73d0b09adfa44414f00-ffffff-000000-0.png)
 in
in 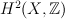 )
)