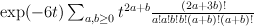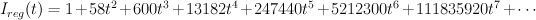Statistics
Notations:
p.s. – period sequence
fano p.s. – one of 105 p.s. of smooth Fano 3-folds
good p.s. – p.s. s.t. P_0(D) has integer roots, where L = sum_{i=0}^r t^i P_i(D) is the diff.op. annihilating p.s.
bad p.s. – not good p.s.
LP – Laurent polynomial.
fano LP – Laurent polynomial for which RG coincides with one of 105 fano p.s.
Everywhere below we put a binomial condition (of Coates-Corti-Galkin-Golyshev-Przjyalkowski-Usnich-etc) on the edges.
MP – Minkowski Laurent polynomial
PP – (Coates-)Przyjalkowski Laurent polynomial (binomial on edges, zero everywhere else)
This is the statistics of reflexive 3-polytopes.
—
18 are smooth.
—
100 (= 18+82) are terminal. They give rise to 100 LP and 62 good p.s.
—
899 (= 18+82+799) has no integer points in interior of facets.
Each one gives rise to a unique MP (which coincides with PP).
712 of these MPs are fano LP – they give rise to 92 fano p.s.
187 are bad – they give rise to 63 bad p.s.
92 = 98-6, where 98 = 105-7.
The 7 that didn’t appear among MP p.s.’s are:
V_2 [bottom degree],
its double cover B_1 [bottom degree in rho=1, r=2],
2.1, 2.2, 2.3 [bottom degree in rho=2],
P^1 x S_2, P^1 x S_1 [top Picard rank].
The extra 6 Fano (p.s.) that didn’t appear are:
V_4 (15), V_6 (19), V_8 (5), V_{10} (9), V_{12} (7) [next bottom degree in rho=1,r=1);
2.4 (49) [next bottom degree in rho=2].
So they lie at the bottom of the list, just over the non-appearing 5.
—
1051 polytopes has exactly one integer point in the respective interior of the facets (i.e. not origin, vertex, and not on the edge).
The facet that contains the extra integer point is then on of famous 16 reflexive 2-polytopes,
so 1051 polytopes fall into 16 classes.
Number of polytopes in each class is as follows (total 1051):
[20, 24, 125, 50, 75, 196, 22, 86, 111, 74, 64, 112, 19, 42, 23, 8]
Number of fano LP in each class is as follows (total 1055):
[0, 20, 0, 47, 61, 187, 27, 123, 195, 140, 56, 109, 17, 42, 23, 8]
which is
[0,17+3,0,44+3,61,187,16+11,71+52,107+88,70+70,56,109,17,42,23,8]
Our enumeration and “fano” values for the extra coefficient are as follows:
number – associated vertex Laurent polynomial – class – #poly – values [number of appearances]
0 – x+y+1/x/y – P^2 – 20 – nothing
1 – y + x/y + 1/x/y – Q – 24 – 0 [17], 4 [3]
2 – x+y+xy+1/x/y – S_8 – 125 – nothing
3 – x+y+1/x+1/y – Q – 50 – 0 [44], 4 [3]
4 – y+x+x/y+1/x/y – S_7 – 75 – 1 [61]
5 – x+y+1/x+1/y+xy – S_7 – 196 – 1 [187]
6 – y/x+1/x/y+x^2/y – S_6 – 22 – 2 [16], 3 [11]
7 – y+y/x+1/x/y+x/y – S_6 – 86 – 2 [71], 3 [52]
8 – y+x+1/x+x/y+1/x/y – S_6 – 111 – 2 [107], 3 [88]
9 – x+y+x/y+1/x+1/y+y/x – S_6 – 74 – 2 [70], 3 [70]
10- x+y/x+1/x/y+x^2/y – S_5 – 64 – 3 [56]
11- x+y+y/x+x/y+1/x+1/y+1/x/y – S_5 – 112 – 3 [109]
12- y+x+1/x+x^2/y+1/x^2/y – S_4 – 19 – 4 [17]
13- y+y/x+1/x/y+x^2/y – S_4 – 42 – 4 [42]
14- xy+y/x+x/y+1/x/y – S_4 – 23 – 4 [23]
15- 1/x/y+x^2/y+y^2/x – S_3 – 8 – 6 [8]
Of course everything is extremal and Hodge-Tate,
but some are not-Minkowski, and not even SCR-equivalent (using only surface mutations of the respective facet) to any Minkowski
(in particular examples with class Q and coefficient a=4,
also those in Q with coeff a=0 are not lattice Minkowski, but Minkowski).
1-puzzles
 and many other Fano threefolds.
and many other Fano threefolds.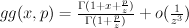 is the familiar Gamma-factor with
is the familiar Gamma-factor with 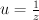 .
.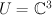 with a fixed base, 7-dimensional vector space
with a fixed base, 7-dimensional vector space 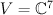 , and space
, and space 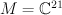 of 3×7 matrices
of 3×7 matrices 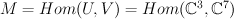
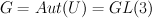 acts on M by left multiplication. It has a subgroup
acts on M by left multiplication. It has a subgroup 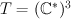 of diagonal matrices and one may restrict the action to this smaller subgroup.
of diagonal matrices and one may restrict the action to this smaller subgroup.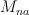 be the subset of matrices of maximal rank and
be the subset of matrices of maximal rank and 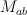 be the subset of matrices with non-vanishing rows,
be the subset of matrices with non-vanishing rows, 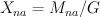 and
and 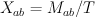 . Note that
. Note that 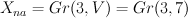 and
and 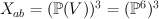 .
.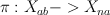 : a triple of points in
: a triple of points in  is sent to their linear span.
is sent to their linear span.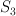 ) acts on
) acts on 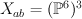 and hence it acts on the cohomology
and hence it acts on the cohomology 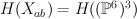 , so cohomology space is decomposed into representations of
, so cohomology space is decomposed into representations of 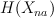 can be identified with antisymmetric part of
can be identified with antisymmetric part of 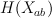 as a graded vector space (with grading shifted by 3).
as a graded vector space (with grading shifted by 3). of hyperplane sections on
of hyperplane sections on  by pulling them back to M, and considering as G-linearized.
by pulling them back to M, and considering as G-linearized. .
. and
and  .
.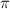 one may define a relative tangent bundle
one may define a relative tangent bundle 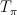 (“traceless” part of
(“traceless” part of 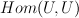 ). It turns out this vector bundle can be extended as a split vector bundle to whole
). It turns out this vector bundle can be extended as a split vector bundle to whole 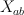 :
: 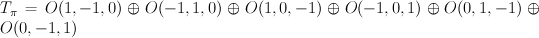 .
.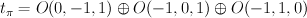 .
.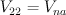 are sections of homogeneous vector bundle
are sections of homogeneous vector bundle 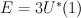 on
on 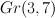 . Comparision (2) shows these threefolds has 9-dimensional abelianizations
. Comparision (2) shows these threefolds has 9-dimensional abelianizations 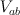 — complete intersections of $9$-dimensional split bundle
— complete intersections of $9$-dimensional split bundle 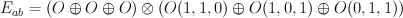 on
on 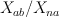 and
and 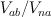 .
.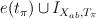 after the comparision of cohomologies described in (1).
after the comparision of cohomologies described in (1).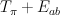 I-series
I-series 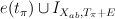 after the “pullbacked” comparision (1).
after the “pullbacked” comparision (1).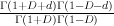 . Since
. Since 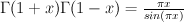 and
and  we have
we have 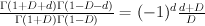 .
.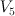 , #2.14, #2.17, #2.20, #2.21 and #2.22.
, #2.14, #2.17, #2.20, #2.21 and #2.22. . This interpretation is more useful for dealing with Frobenius manifolds.
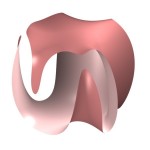
. This interpretation is more useful for dealing with Frobenius manifolds.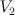 seen from several different angles.
seen from several different angles. 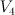 seen from two different angles.
seen from two different angles. 

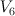










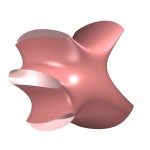


 as follows.
as follows.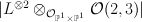 on the
on the  -bundle
-bundle  over
over 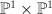 such that
such that  is irreducible, where
is irreducible, where  is the tautological line bundle and
is the tautological line bundle and 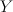 is a member of
is a member of 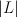 .
.  is the toric variety with weight data:
is the toric variety with weight data: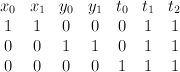
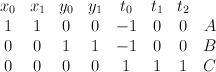
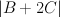 .
.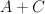 (which restricts to
(which restricts to 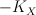 on
on 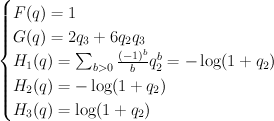


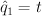 ,
, 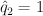 ,
, 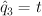 ,
, 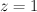 yields:
yields: