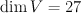Beyond Minkowski ansatz
There are two examples of correct polynomials that don’t fit into ansatz stated below.
I think I have shown these examples to Alessio in April.
More info in the notes of my talk (page 2, polynomials 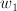 and
and 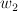 ): pdf (or follow the link from here).
): pdf (or follow the link from here).
Both examples are degenerations of projective space 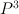 (grdb[547386]).
(grdb[547386]).
================================================================================
Period sequence 12
First 10 period coefficients: [1, 0, 0, 0, 24, 0, 0, 0, 2520, 0]
The PF operator has N=3, r=4
This sequence has a smooth toric Fano representative
It arises from the following polytopes [(PALP id, grdb id, smoothness)]:
(0, 547386, ‘smooth’)
The PF operator for this sequence is:
256*t^4*D^3 + 1536*t^4*D^2 + 2816*t^4*D + 1536*t^4 – D^3
================================================================================
So we start from the familiar Laurent polynomial
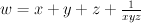
I. Argument against “lattice” decomposition.
a. make monomial transformation

w goes to 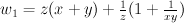
b. mutate by
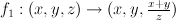
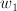 goes to
goes to 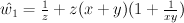
Since 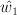 is derived from w by transformation from group
is derived from w by transformation from group 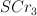 it is a mirror for projective space
it is a mirror for projective space 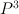 (“weak Landau-Ginzburg model” in Przyalkowski’s notations).
(“weak Landau-Ginzburg model” in Przyalkowski’s notations).
Newton polygon of 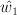 is fan polytope of a Gorenstein toric variety – (grdb[544357]).
is fan polytope of a Gorenstein toric variety – (grdb[544357]).
This variety is anticanonical cone over smooth quadric 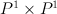 , i.e. a cone over section of
, i.e. a cone over section of 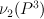 (
(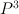 embedded into
embedded into 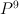 by complete linear system of quadrics),
by complete linear system of quadrics),
and hence it is a geometric degeneration of 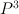 .
.
Consider the quadrangular face, corresponding to a singular point. Restriction of 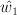 to this face is
to this face is 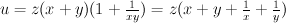 . It is not friendly to Minkowski ansatz’s condition of lattice Minkowski decomposition (this is exactly the example of Minkowski decomposition that is not a lattice Minkowski decomposition given in the definition of the ansatz).
. It is not friendly to Minkowski ansatz’s condition of lattice Minkowski decomposition (this is exactly the example of Minkowski decomposition that is not a lattice Minkowski decomposition given in the definition of the ansatz).
II. Argument against “admissible triangles” and decomposing polytopes completely.
Example 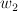 from the same notes.
from the same notes.
This one is degeneraiton to 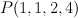 (grdb[547363]).
(grdb[547363]).
By monomial transformation
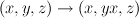
transform w to

then by mutation
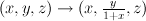
transform 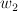 to
to
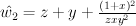
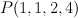 is embedded as a quadric in
is embedded as a quadric in 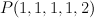 by linear system
by linear system 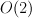 , so it is a degeneration of a general quadric in this space i.e.
, so it is a degeneration of a general quadric in this space i.e. 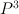 .
.
This variety 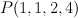 is also the anticanonical cone over singular quadratic surface
is also the anticanonical cone over singular quadratic surface 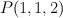 .
.
Restriction to the face equivalent to this surface is equal to
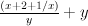 , so it is not admissible.
, so it is not admissible.
Z. How to tune the ansatz?
Universal fix:
allow change of the lattice after creating some of the good polynomials
less universal:
a. Allow non-lattice Minkowski decompositions
AND/OR
b. Increase the set of admissible figures
Update on June 22:
III. Examples further beyond
By combining technique from examples in this and previous post we can construct some more sophisticated
mirrors for Tom and Jerry. These mirrors should correspond to degenerations of these guys to Gorenstein cones over singular (Gorenstein or not) del Pezzo surfaces of degree 6.
I’ll write only numerical details and maybe will provide some geometry later in the comment.
Start from a honeycomb and

Using cluster transformations it can be transformed to mirrors constructed from Gorenstein toric degenerations of del Pezzo surface  .
.
first to pentagon
then to quadruple
then to triangle
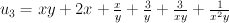
The triangle is fan polytope of Gorenstein weighted projective plane P(1,2,3).
We can mutate it further to get non-Gorenstein weighted projective plane P(1,3,8)
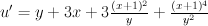
Then we choose G equal to 2 or 3
and take
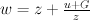
This will be weak mirror for Jerry or Tom,
all underlying toric threefolds are Gorenstein.
Last two are P(1,2,3,6) (grdb[547331]) and P(1,3,8,12) (grdb[547474]).
Triangles may be Minkowski decomposable only when they are multiples of smaller triangles, which is not the case in these examples.
Altmann’s results on relations between Minkowski decompositions and deformations does not apply here since we have non-isolated singularity (it is a cone over already singular space).
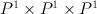
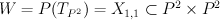 (hyperplane section of product of two planes in Segre embedding).
(hyperplane section of product of two planes in Segre embedding).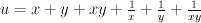
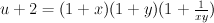
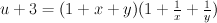
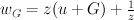
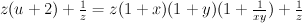
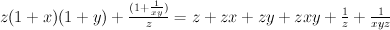
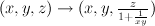 .
.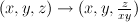 :
: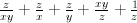
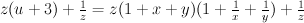
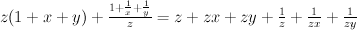
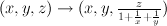
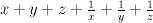
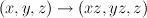 .
.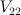 can be characterized as the smooth Fano of index 1 with minimal cohomology. One way to construct its D3 is by assigning 1’s to the vertices of a terminal self-dual polytope.
can be characterized as the smooth Fano of index 1 with minimal cohomology. One way to construct its D3 is by assigning 1’s to the vertices of a terminal self-dual polytope.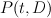 annilihating the principal period such that
annilihating the principal period such that 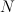 in
in 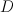 and
and  in
in 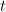 , where
, where 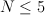 and
and 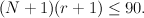 The results were:
The results were: be a 3-dimensional reflexive polytope. We will construct a Laurent polynomial with Newton polytope equal to
be a 3-dimensional reflexive polytope. We will construct a Laurent polynomial with Newton polytope equal to  is the lattice Minkowski sum of polygons
is the lattice Minkowski sum of polygons 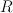 and
and 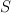 if and only if both:
if and only if both: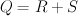 , so that
, so that  here are allowed to be degenerate.
here are allowed to be degenerate.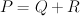 of a hexagon:
of a hexagon:

 :
:
 .
. of
of 
 of Laurent polynomials; this list will be empty if
of Laurent polynomials; this list will be empty if 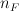 elements in the list for facet
elements in the list for facet  ).
). as a piece of the quantum cohomology local system associated to a smoothing of the Newton polytope of
as a piece of the quantum cohomology local system associated to a smoothing of the Newton polytope of