Let X be a smooth Fano threefold with Picard number P = 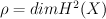 .
.
Then subring of algebraic (even) cycles in X is (2+2P)-dimensional, and its Lefschetz decomposition has P blocks: 1 block of length 4 and (P-1) blocks of length 2. So its image in cohomologies of anticanonical section (K3 surface) is (2+2P – P) = (2+P)-dimensional.
For “general” Fano threefold with Picard number P we expect
regularized quantum differential equation (RQDE) to be of degree (2+P) in 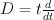
and to have (2+2P) singular points. Nevertheless degree in t may be more than number of singular points
due to apparent singularities.
It turns out that condition for general is not very general in practice.
Assume Fano threefold X has action of finite group G in one of the 4 ways:
a. G acts on X by regular (algebraic) transformations,
b. G acts on X by symplectic transformations,
c. X is defined over non-algebraically closed field k and G is Galois group Gal(k),
d. X is a fiber of a smooth family over some base B and fundamental group 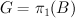 acts on
acts on 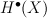 via monodromy.
via monodromy.
For cases a,b,c consider the induced action of G on cohomology of X.
Let p = 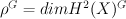 be $G$-invariant Picard number.
be $G$-invariant Picard number.
G-invariant part of cohomologies 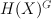 is (2+2p)-dimensional.
is (2+2p)-dimensional.
Define  of
of  as subring generated by
as subring generated by  and C[t].
and C[t].
It is easy to see 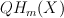 is contained in
is contained in ![H(X, C)^G [t] H(X, C)^G [t]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/f66/f66c236b83bd71fc79b4f33e0ef3c4a4-ffffff-000000-0.png) .
.
This implies that regularized I-series 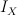 is annihilated by
is annihilated by
differential operator of degree (2+p).
So it is natural to ask about possible G-actions on Fano threefolds.
First (numerical) step is to see the possible automorphisms of Mori cone or Kaehler cone.
We have some structures on 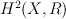 :
:
a. lattice 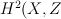 ) and element
) and element  inside the lattice,
inside the lattice,
b. rational polyhedral cone of numerically effective divisors,
c. nondegenerate integral quadratic form (Lefschetz pairing) : 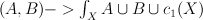 .
.
We call this information 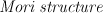 .
.
Group of automorphisms of Mori structure is finite, and for any action
G-invariant Picard number is not less than dimension of invariants of 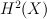
with respect to whole group of automorphisms of Mori structure.
As far as I remember (but cannot find a reference) for all Fano threefolds one may find some moduli
and some kind of G-action such that G-invariant Picard group coincides with invariant part of $H^2$ with respect to automorphisms of Mori structure.
The standard reference for automorphisms of Mori structure is probably:
Kenji Matsuki, “Weyl groups and birational transformations among minimal models”, AMS 1995
He studies slightly different problem, but has a similar answer. Unfortunately I haven’t a copy of this book, but copied one page from google books.
He says automorphisms of Mori structures turn out to be Weyl groups.
He claims the following Fano threefolds have nontrivial automorphisms:
P – Picard number, then list of Mori-Mukai numbers with the given Picard number
P=2:
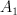 : 2, 6, 12, 21, 32 (these should be G-Fano, but number 2 is suspicious)
: 2, 6, 12, 21, 32 (these should be G-Fano, but number 2 is suspicious)
other have p=2
P=3:
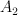 : 1, 27 (G-Fano, suspicious that 13 is in the next line)
: 1, 27 (G-Fano, suspicious that 13 is in the next line)
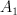 : 3, 7, 9, 10, 13, 17, 19, 20, 25, 31 (should correspond to p=2)
: 3, 7, 9, 10, 13, 17, 19, 20, 25, 31 (should correspond to p=2)
other have p=3
P=4:
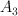 : 1 (G-Fano)
: 1 (G-Fano)
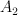 : 6 (p=2)
: 6 (p=2)
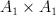 : 2 (p=2)
: 2 (p=2)
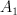 : 3, 4, 7, 8, 10, 12 (p=3)
: 3, 4, 7, 8, 10, 12 (p=3)
trivial – 5,9,11 (should have p=4)
missing number 13 from Erratum
P=5:
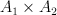 : 3 (p=2)
: 3 (p=2)
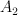 : 1 (p=3)
: 1 (p=3)
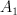 : 2 (p=4)
: 2 (p=4)
For cases 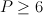 our threefolds are products of a line and del Pezzo surface
our threefolds are products of a line and del Pezzo surface  . They all have Weyl group of type
. They all have Weyl group of type 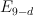 and p=2.
and p=2.
So the distribution in p is the following (case 4.13 is missing):
p is always less than 5;
p=4 – 4 varieties: 5.2; 4.5, 4.9, 4.11
p=3 – 26 varieties: 5.1; 4.3, 4.4, 4.7, 4.8, 4.10, 4.12; and 19 with P=3
p=2 – 50 varieties
p=1 – 25 varieties (or 26 if 2.2 is there)
This means just 4 varieties should have N=6, and other have even less.
The obvious thing to do is to recompute ourselves the Mori structure and its automorphisms
(in particular discriminant of Lefschetz quadratic form is an important invariant that we need anyway).
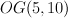
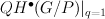 (Chaput–Manivel–Perrin) and connections to work of Kostant (Gorbunov–Petrov)
(Chaput–Manivel–Perrin) and connections to work of Kostant (Gorbunov–Petrov)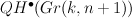
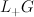 -orbits in the affine Grassmannian
-orbits in the affine Grassmannian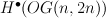 and
and 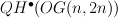
 is rational of dimension
is rational of dimension 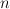 implies that the spectrum of
implies that the spectrum of 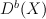 has no gaps of size greaeter than
has no gaps of size greaeter than 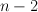
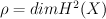 .
.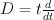
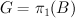 acts on
acts on 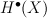 via monodromy.
via monodromy. 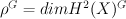 be $G$-invariant Picard number.
be $G$-invariant Picard number.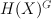 is (2+2p)-dimensional.
is (2+2p)-dimensional. of
of 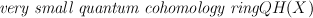 as subring generated by
as subring generated by  and C[t].
and C[t].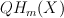 is contained in
is contained in ![H(X, C)^G [t] H(X, C)^G [t]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/f66/f66c236b83bd71fc79b4f33e0ef3c4a4-ffffff-000000-0.png) .
.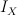 is annihilated by
is annihilated by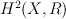 :
: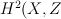 ) and element
) and element 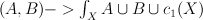 .
. .
.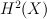
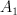 : 2, 6, 12, 21, 32 (these should be G-Fano, but number 2 is suspicious)
: 2, 6, 12, 21, 32 (these should be G-Fano, but number 2 is suspicious)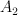 : 1, 27 (G-Fano, suspicious that 13 is in the next line)
: 1, 27 (G-Fano, suspicious that 13 is in the next line)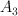 : 1 (G-Fano)
: 1 (G-Fano)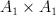 : 2 (p=2)
: 2 (p=2)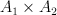 : 3 (p=2)
: 3 (p=2)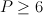 our threefolds are products of a line and del Pezzo surface
our threefolds are products of a line and del Pezzo surface  . They all have Weyl group of type
. They all have Weyl group of type 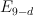 and p=2.
and p=2.