Archive for the ‘Uncategorized’ Category.
December 3, 2010, 2:19 pm
Consider the blow-up  of
of 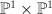 with center a complete intersection of type
with center a complete intersection of type 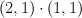 . Since the complete intersection consists of three points,
. Since the complete intersection consists of three points,  is a del Pezzo surface
is a del Pezzo surface 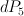 . It is tempting to compute its regularized period sequence as follows.
. It is tempting to compute its regularized period sequence as follows.
Warning: this calculation is wrong. I explain below where the error is and how to fix it. We express  as a complete intersection in a toric variety
as a complete intersection in a toric variety  as follows. Let
as follows. Let  have weight data:
have weight data:
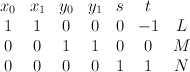
Now consider the equation:
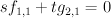
where 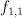 and
and 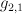 are polynomials in
are polynomials in 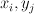 of bidegrees (respectively) (1,1) and (2,1). The variety
of bidegrees (respectively) (1,1) and (2,1). The variety  defined by this equation is cut out by a section of the line bundle
defined by this equation is cut out by a section of the line bundle 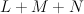 ; by projecting
; by projecting ![[x_0:x_1:y_0:y_1:s:t] \mapsto [x_0:x_1:y_0:y_1] [x_0:x_1:y_0:y_1:s:t] \mapsto [x_0:x_1:y_0:y_1]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/e81/e817d27607809e965cfe4b905bc95bc8-ffffff-000000-0.png) we see that
we see that  is, as desired, the blow-up of
is, as desired, the blow-up of 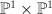 in a complete intersection of type
in a complete intersection of type 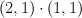 . We have
. We have 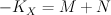 and:
and:
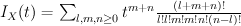
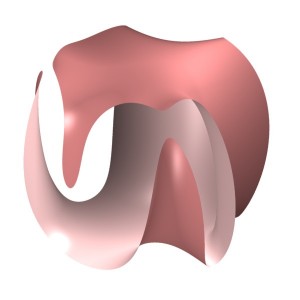
Regularizing gives the period sequence:
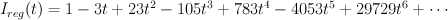
This is not correct: we know the regularized period sequences for del Pezzo surfaces, and in the case of 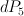 we get:
we get:
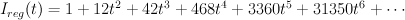
So what went wrong?
The construction of  given above is correct. It is the second half of the calculation which is flawed. The key point is that, even though
given above is correct. It is the second half of the calculation which is flawed. The key point is that, even though  is Fano and is cut out of the ambient space
is Fano and is cut out of the ambient space  by a section of an ample line bundle,
by a section of an ample line bundle, 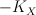 is not the restriction of an ample line bundle on
is not the restriction of an ample line bundle on  but rather is only the restriction of a semi-positive line bundle on
but rather is only the restriction of a semi-positive line bundle on  . Thus the mirror map is non-trivial. To see this we need to consider not Golyshev’s I-function:
. Thus the mirror map is non-trivial. To see this we need to consider not Golyshev’s I-function:
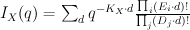
but rather the full Givental I-function:
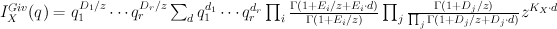
Here  is cut out of the toric variety with toric divisors
is cut out of the toric variety with toric divisors 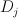 by a section of the direct sum of line bundles
by a section of the direct sum of line bundles 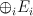 . Golyshev’s I-function is obtained from Givental’s I-function by taking the term in cohomological degree zero and setting:
. Golyshev’s I-function is obtained from Givental’s I-function by taking the term in cohomological degree zero and setting:
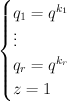
where 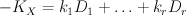 . Note that Givental’s I-function is homogeneous of degree zero if we set
. Note that Givental’s I-function is homogeneous of degree zero if we set 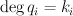 ,
, 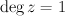 , and
, and 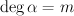 whenever
whenever 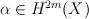 .
.
In the situation at hand (i.e.  is a semipositive complete intersection in a toric variety) we have, for grading reasons:
is a semipositive complete intersection in a toric variety) we have, for grading reasons:
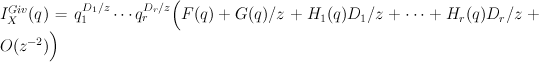
where 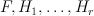 are degree-zero power series in the
are degree-zero power series in the 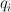 and
and 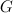 is a degree-1 power series in the
is a degree-1 power series in the 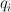 . Furthermore Givental’s mirror theorem states that:
. Furthermore Givental’s mirror theorem states that:

where:
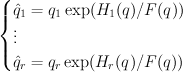
This change of variables is called the mirror map. The regularized quantum period sequence that we seek is obtained from the cohomological-degree-zero component of the J-function by setting 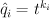 ,
, 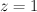 , and doing the trick with factorials:
, and doing the trick with factorials: 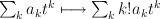 .
.
Applying this discussion in our case (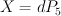 realized as above) yields:
realized as above) yields:
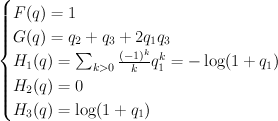
and hence:
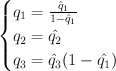
Thus the cohomological-degree-zero part of the J-function is:

and setting 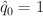 ,
, 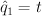 ,
, 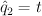 ,
, 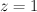 yields:
yields:
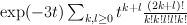
Regularizing this gives:
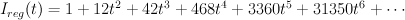
which agrees with our previous calculation.
December 3, 2010, 12:25 pm
November 22, 2010, 2:10 pm
November 16, 2010, 4:19 pm
October 13, 2010, 1:14 pm
I’ve fixed a bug in the wp-LaTeX plug-in which was preventing certain matrices displaying correctly. All the LaTeX output on the site now appears to render correctly.
October 9, 2010, 7:54 pm
I’ve set up a Twitter account @fanosearch and arranged for blog entries and comments to appear automatically as tweets. Also results of major computer calculations will appear as tweets (or at least they will once I’ve figured out how to use the Twitter API from Sage).
If you have a Twitter account, you can follow @fanosearch to get these updates. Or you can get them direct from your web browser by subscribing to this RSS feed. If you prefer to get the blog posts and comments separately then you can use these RSS feeds (posts, comments) which come direct from the blog. To add the @fanosearch Twitter feed to Facebook, use this.
September 22, 2010, 12:09 pm
Here are my (incomplete) notes from Batyrev’s talk in the Extremal Laurent Polynomials workshop at Imperial:
Batyrev_London_Sep_2010
If you have complete notes, please post them here.
Partial summary:
- spherical varieties
- a model family of examples:
 -varieties
-varieties
- review: compactification and toric varieties
- spherical compactification in these examples
- valuations and coloured cones
- finding toric degenerations
September 22, 2010, 12:04 pm
Here are my notes from Altmann’s talk at the Extremal Laurent Polynomials workshop at Imperial:
Altmann_London_Sep_2010
Summary:
- an example due to Pinkham
- deformations and Minkoski sums; a lattice condition
- constructing the deformation corresponding to a Minkwoski decomposition
- the versal deformation space and the moduli space of generalized Minkowski summands of Q
- Example: the cone over a hexagon
- the equations defining the versal deformation space in the isolated Gorenstein case
- a new point of view: double divisors
September 22, 2010, 11:58 am
Here are my notes from Siebert’s talk at the Extremal Laurent Polynomials workshop at Imperial:
Siebert_London_Sep_2010
Summary:
- An overview of toric degenerations and the Gross–Siebert picture
- Examples: a pencil of quartics in
 and a pencil of elliptic curves in
and a pencil of elliptic curves in 
- the Gross–Siebert Reconstruction Theorem
- Mirror Symmetry and the discrete Legendre Transform
- Landau–Ginzburg models; the Hori–Vafa mirror
- how to extend the superpotential from the central fiber to the whole of the mirror family in such a way that the resulting superpotential is proper
- Example:
 , flattening the boundary of the polyhedral complex
, flattening the boundary of the polyhedral complex
- Broken lines and scattering
September 22, 2010, 11:50 am
Here are my notes from Golshev’s talk at the Extremal Laurent Polynomials workshop at Imperial:
Golyshev_London_Sep_2010
Summary:
- a historical analogy: the study of Fano varieties now versus the study of algebraic varieties in the early 1970s
- the key idea: classifying Fanos by detecting and classifying Fano quantum motives and their realizations
- possible approaches
- the Tannakian picture
- the quantum Satake correspondence (Golyshev–Manivel)
- two steps in this direction: Ueda’s proof of the Dubrovin Conjecture for
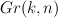 ; Galkin–Golyshev–Iritani’s proof that Apery=Gamma
; Galkin–Golyshev–Iritani’s proof that Apery=Gamma
- irregular monodromy data for Dubrovin’s quantum connection
- the Extended Dubrovin Conjecture and the Apery=Gamma hypothesis
- the Extended Dubrovin Conjecture and the Apery=Gamma hypothesis hold for
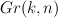
 of
of 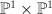 with center a complete intersection of type
with center a complete intersection of type 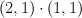 . Since the complete intersection consists of three points,
. Since the complete intersection consists of three points,  is a del Pezzo surface
is a del Pezzo surface 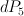 . It is tempting to compute its regularized period sequence as follows.
. It is tempting to compute its regularized period sequence as follows. as a complete intersection in a toric variety
as a complete intersection in a toric variety  as follows. Let
as follows. Let  have weight data:
have weight data: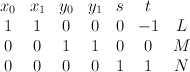
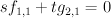
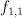 and
and 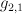 are polynomials in
are polynomials in 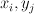 of bidegrees (respectively) (1,1) and (2,1). The variety
of bidegrees (respectively) (1,1) and (2,1). The variety  defined by this equation is cut out by a section of the line bundle
defined by this equation is cut out by a section of the line bundle 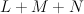 ; by projecting
; by projecting ![[x_0:x_1:y_0:y_1:s:t] \mapsto [x_0:x_1:y_0:y_1] [x_0:x_1:y_0:y_1:s:t] \mapsto [x_0:x_1:y_0:y_1]](http://coates.ma.ic.ac.uk/fanosearch/wp-content/latex/e81/e817d27607809e965cfe4b905bc95bc8-ffffff-000000-0.png) we see that
we see that  is, as desired, the blow-up of
is, as desired, the blow-up of 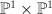 in a complete intersection of type
in a complete intersection of type 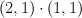 . We have
. We have 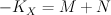 and:
and: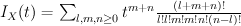
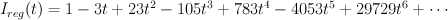
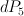 we get:
we get: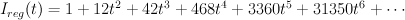
 given above is correct. It is the second half of the calculation which is flawed. The key point is that, even though
given above is correct. It is the second half of the calculation which is flawed. The key point is that, even though  is Fano and is cut out of the ambient space
is Fano and is cut out of the ambient space  by a section of an ample line bundle,
by a section of an ample line bundle, 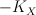 is not the restriction of an ample line bundle on
is not the restriction of an ample line bundle on  but rather is only the restriction of a semi-positive line bundle on
but rather is only the restriction of a semi-positive line bundle on  . Thus the mirror map is non-trivial. To see this we need to consider not Golyshev’s I-function:
. Thus the mirror map is non-trivial. To see this we need to consider not Golyshev’s I-function: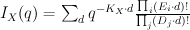
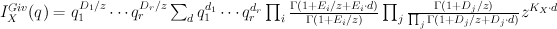
 is cut out of the toric variety with toric divisors
is cut out of the toric variety with toric divisors 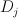 by a section of the direct sum of line bundles
by a section of the direct sum of line bundles 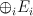 . Golyshev’s I-function is obtained from Givental’s I-function by taking the term in cohomological degree zero and setting:
. Golyshev’s I-function is obtained from Givental’s I-function by taking the term in cohomological degree zero and setting: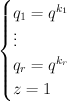
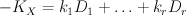 . Note that Givental’s I-function is homogeneous of degree zero if we set
. Note that Givental’s I-function is homogeneous of degree zero if we set 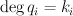 ,
, 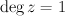 , and
, and 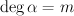 whenever
whenever 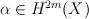 .
. is a semipositive complete intersection in a toric variety) we have, for grading reasons:
is a semipositive complete intersection in a toric variety) we have, for grading reasons: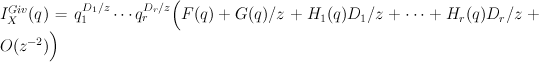
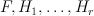 are degree-zero power series in the
are degree-zero power series in the 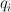 and
and 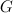 is a degree-1 power series in the
is a degree-1 power series in the 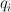 . Furthermore Givental’s mirror theorem states that:
. Furthermore Givental’s mirror theorem states that:
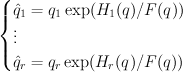
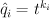 ,
, 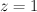 , and doing the trick with factorials:
, and doing the trick with factorials: 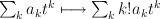 .
.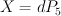 realized as above) yields:
realized as above) yields: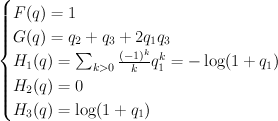
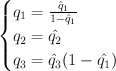

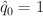 ,
, 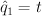 ,
, 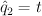 ,
, 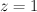 yields:
yields: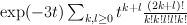




 , choose an affine chart on
, choose an affine chart on 

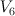







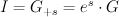 )
)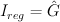 )
) . We have:
. We have: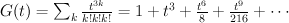
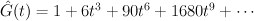
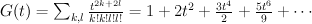
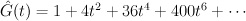
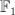 . We have:
. We have: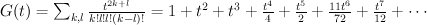
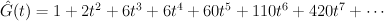
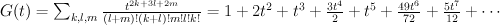
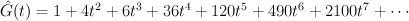
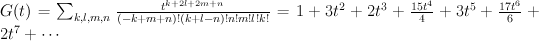
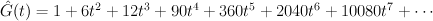
 in
in  . We have:
. We have: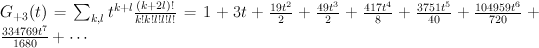
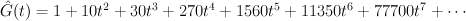
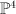 . We have:
. We have:
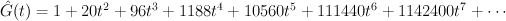
 . We have:
. We have: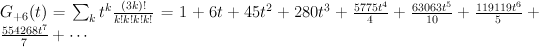
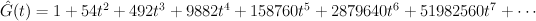
 . We have:
. We have: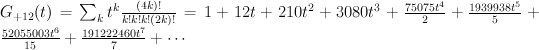
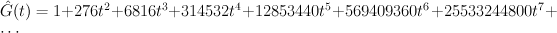
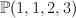 . We have:
. We have: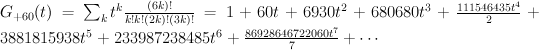
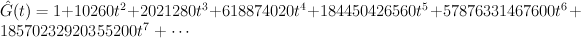
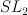 -varieties
-varieties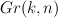 ; Galkin–Golyshev–Iritani’s proof that Apery=Gamma
; Galkin–Golyshev–Iritani’s proof that Apery=Gamma